Extend the class Polynomial below, so that Polynomial objects can be iterated, using a for-loop. Iterating over a Polynomial object p must yield exactly the non-zero terms of p, represented in the form (coefficient, exponent, variable). E.g., for p=Polynomial([2,0,3]), evaluating for i in p should first result in i=(2,0,'x'), then i=(3,2,'x'), and then the loop should end.

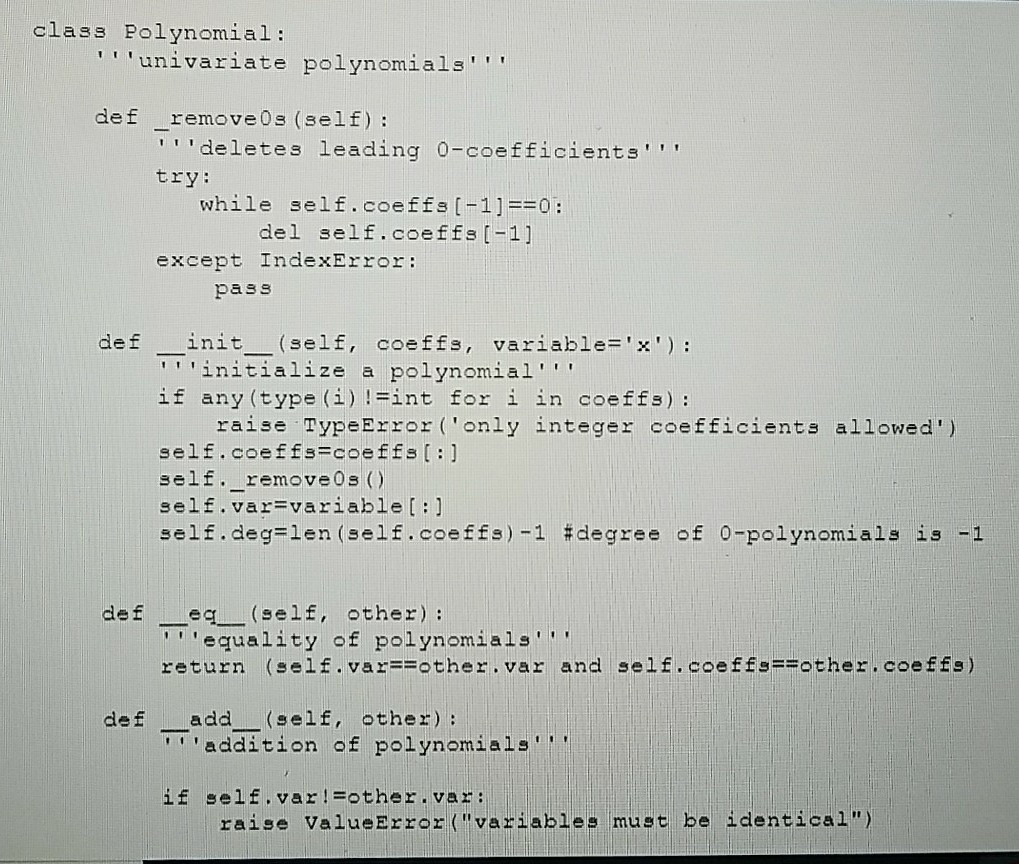
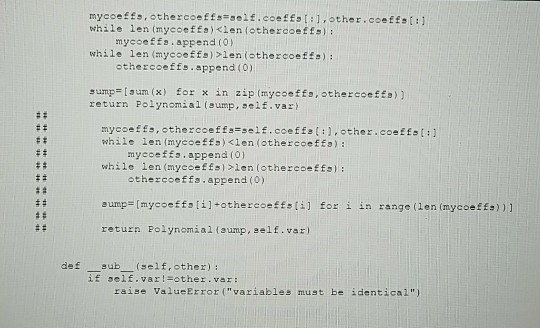
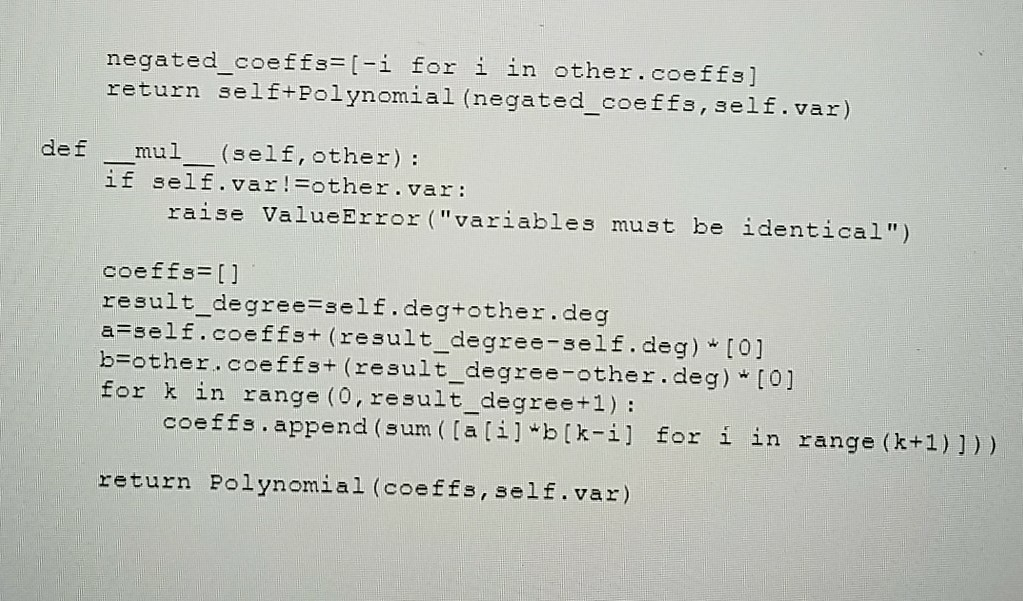
class Polynomial: 'univariate polynomials'' def remove0s (self): 'deletes leading 0-coefficients'' try: while self.coeffs(-1]=#0.: del self.coeffst-1 except IndexError pass der init (self, coeffs, variable='x'): - -- 'initialize a polynomial'" if any (type (i) !=int for i in coeffs) ; raise TypeBrror ('only integer coefficients allowed') self. coeffs=coeffs [ : ] self._remove0s () self.var-variable[:1 self.deg len(self.coeffs)-1 #degree f 0-polynom a 1 s s -1 def eq (self, other) 1 'equality of polynomials''' return (self. var-Fother.var and self.coeffs- other.coeffs) def add (self, other)': ''addition of polynomials if self.vari=ther.va r : raise ValueBrror ("variables must be identical") class Polynomial: 'univariate polynomials'' def remove0s (self): 'deletes leading 0-coefficients'' try: while self.coeffs(-1]=#0.: del self.coeffst-1 except IndexError pass der init (self, coeffs, variable='x'): - -- 'initialize a polynomial'" if any (type (i) !=int for i in coeffs) ; raise TypeBrror ('only integer coefficients allowed') self. coeffs=coeffs [ : ] self._remove0s () self.var-variable[:1 self.deg len(self.coeffs)-1 #degree f 0-polynom a 1 s s -1 def eq (self, other) 1 'equality of polynomials''' return (self. var-Fother.var and self.coeffs- other.coeffs) def add (self, other)': ''addition of polynomials if self.vari=ther.va r : raise ValueBrror ("variables must be identical")