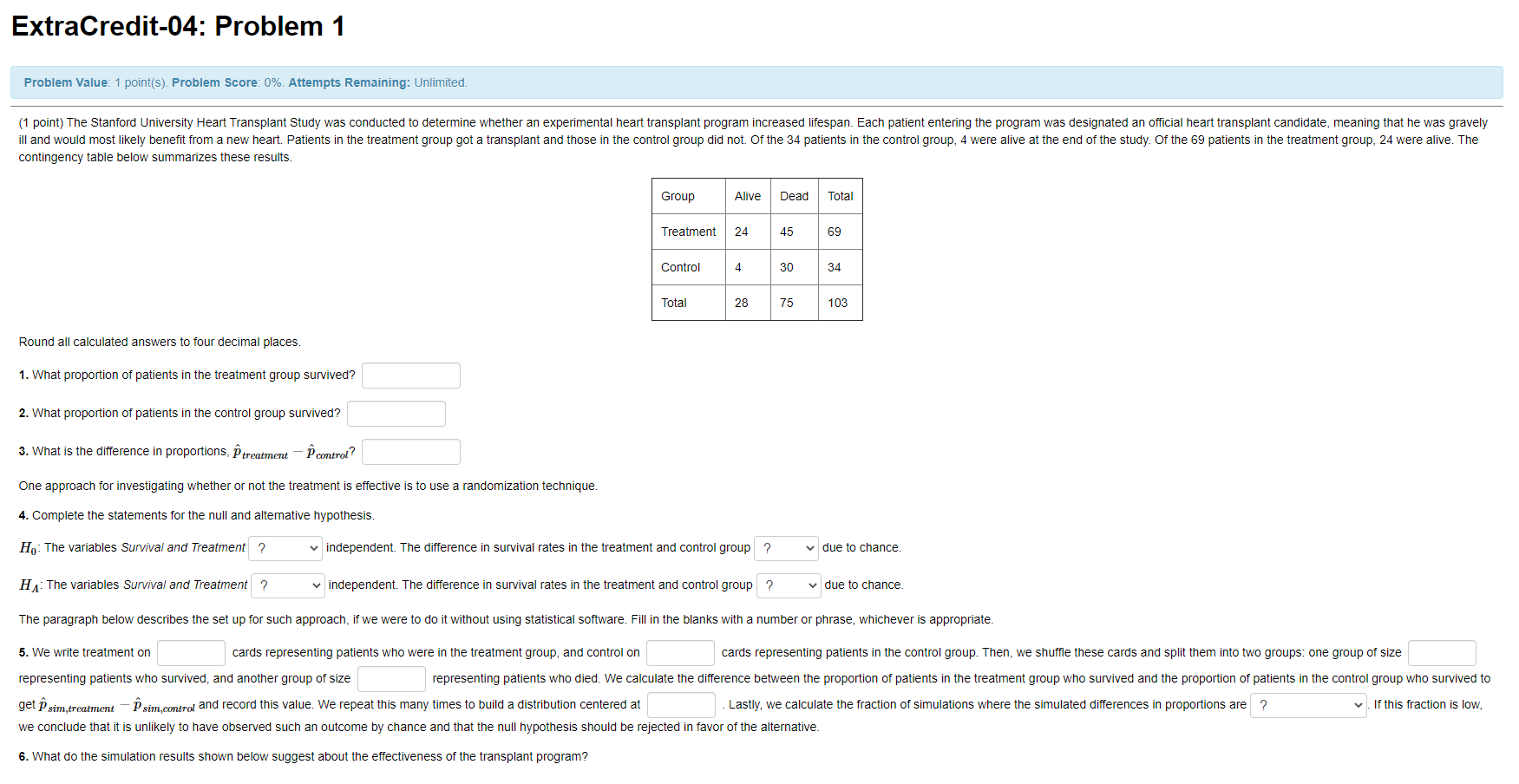
ExtraCredit-04: Problem 1 Problem Value: 1 point(s). Problem Score: 0%. Attempts Remaining: Unlimited. (1 point) The Stanford University Heart Transplant Study was conducted to determine whether an experimental heart transplant program increased lifespan. Each patient entering the program was designated an official heart transplant candidate, meaning that he was gravely ill and would most likely benefit from a new heart. Patients in the treatment group got a transplant and those in the control group did not. Of the 34 patients in the control group, 4 were alive at the end of the study. Of the 69 patients in the treatment group, 24 were alive. The contingency table below summarizes these results. Group Alive Dead Total Treatment 24 45 69 Control 30 34 Total 28 75 103 Round all calculated answers to four decimal places. 1. What proportion of patients in the treatment group survived? 2. What proportion of patients in the control group survived? 3. What is the difference in proportions, Ptreatment - Pcontrol? One approach for investigating whether or not the treatment is effective is to use a randomization technique. 4. Complete the statements for the null and alternative hypothesis. Ho: The variables Survival and Treatment ? independent. The difference in survival rates in the treatment and control group ? due to chance. HA: The variables Survival and Treatment ? independent. The difference in survival rates in the treatment and control group ? v due to chance. The paragraph below describes the set up for such approach, if we were to do it without using statistical software. Fill in the blanks with a number or phrase, whichever is appropriate. 5. We write treatment on cards representing patients who were in the treatment group, and control on cards representing patients in the control group. Then, we shuffle these cards and split them into two groups: one group of size representing patients who survived, and another group of size representing patients who died. We calculate the difference between the proportion of patients in the treatment group who survived and the proportion of patients in the control group who survived to get P sim, treatment - P sim, control and record this value. We repeat this many times to build a distribution centered at . Lastly, we calculate the fraction of simulations where the simulated differences in proportions are|? v. If this fraction is low, we conclude that it is unlikely to have observed such an outcome by chance and that the null hypothesis should be rejected in favor of the alternative. 6. What do the simulation results shown below suggest about the effectiveness of the transplant program