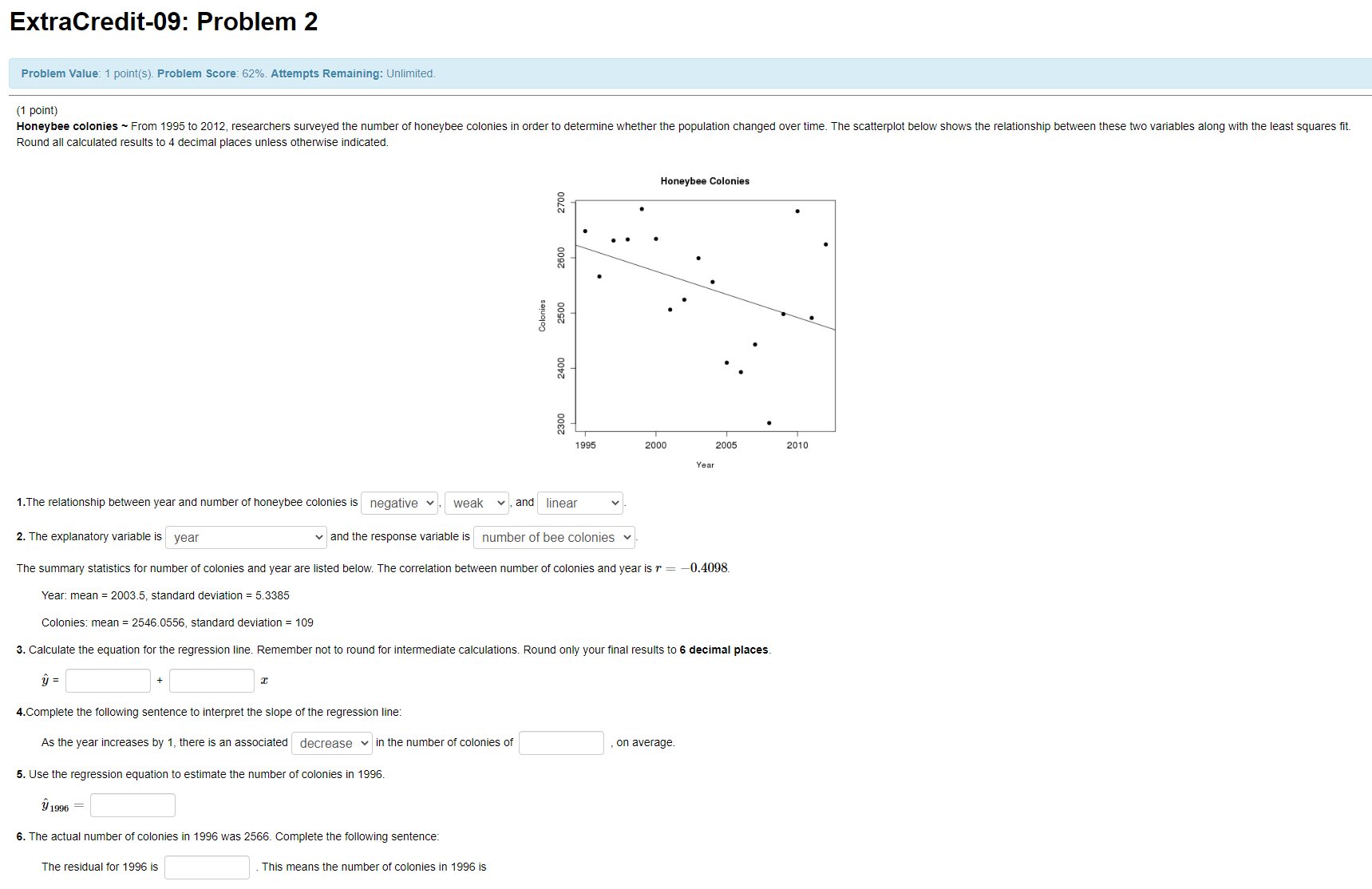
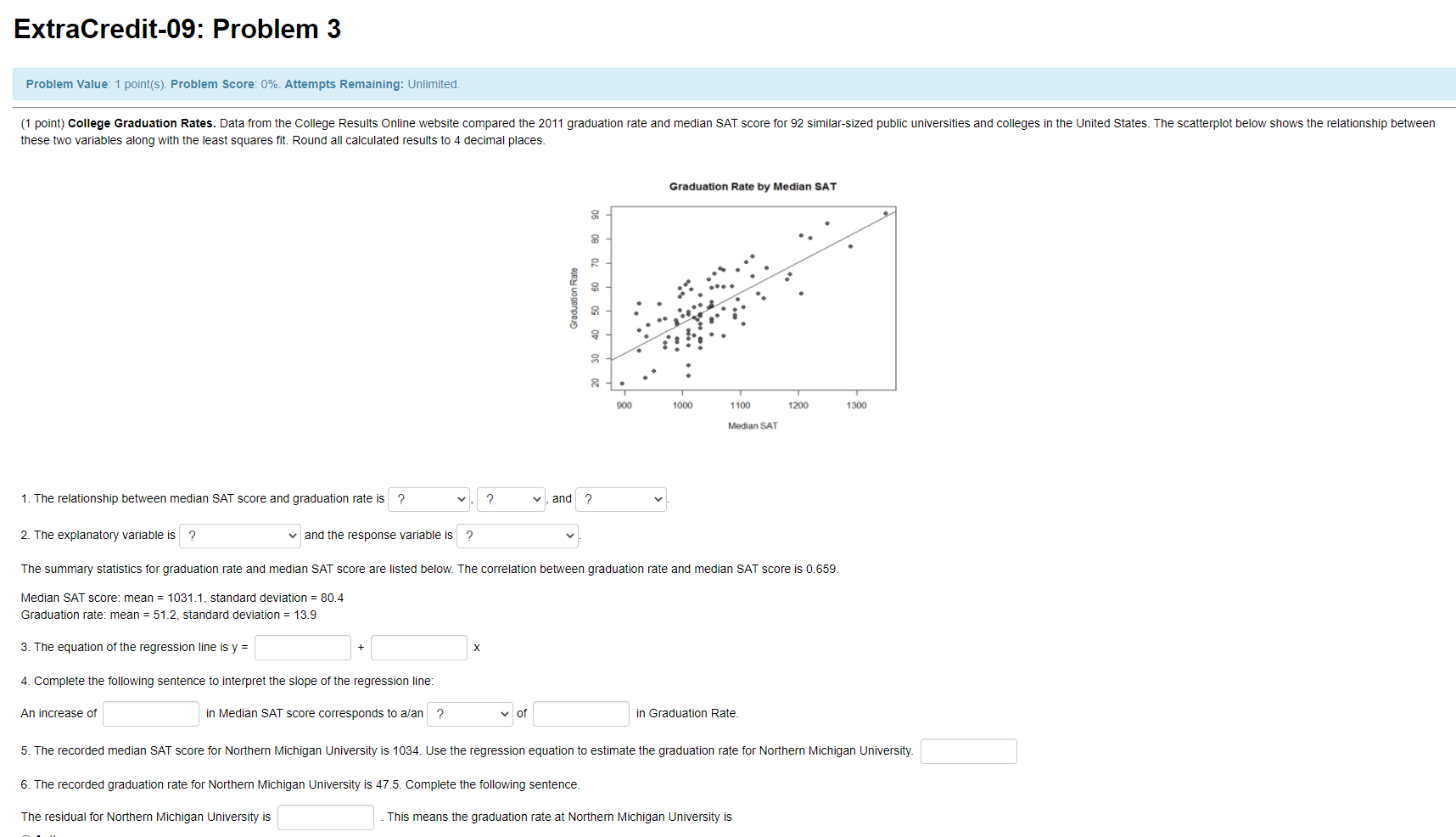
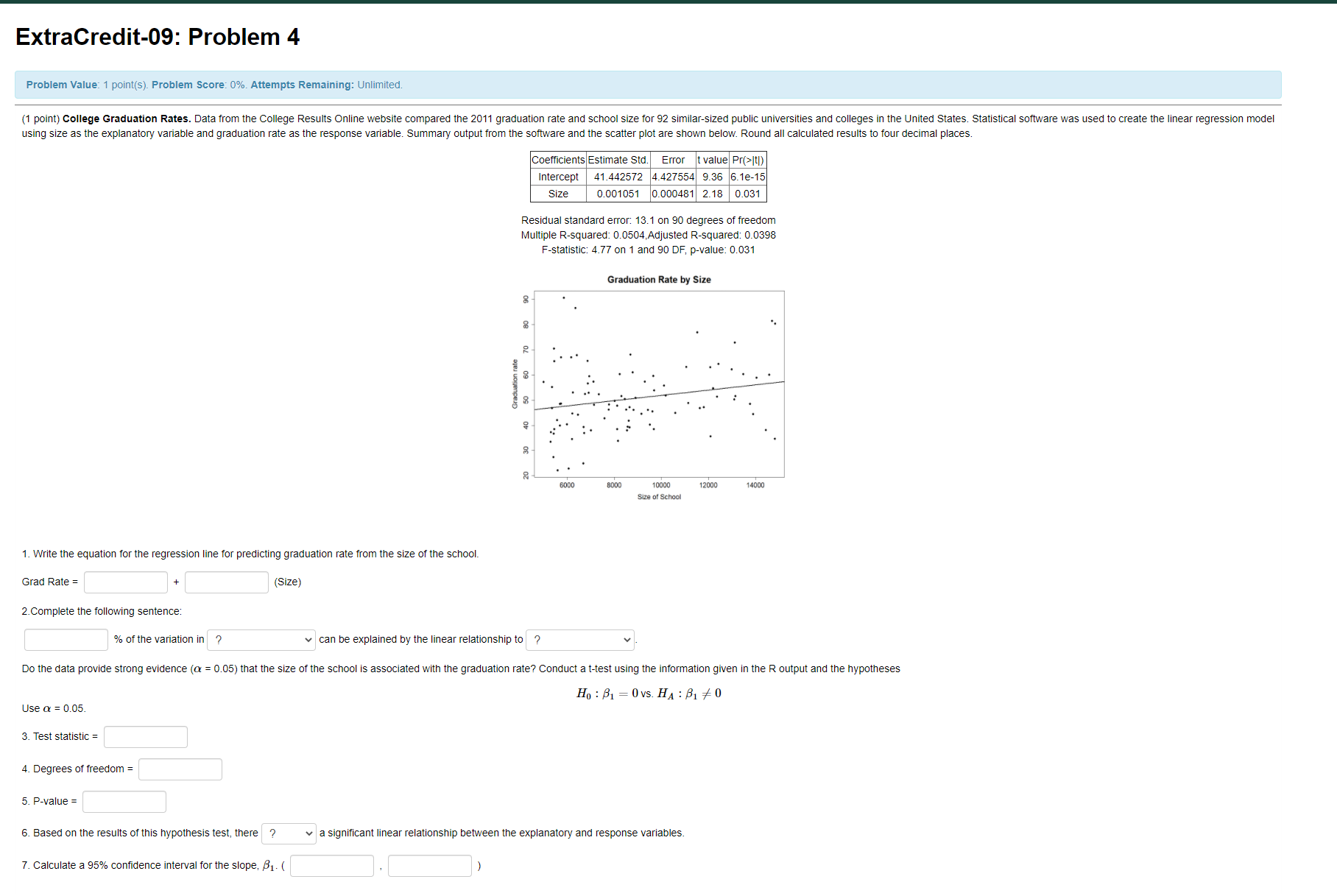
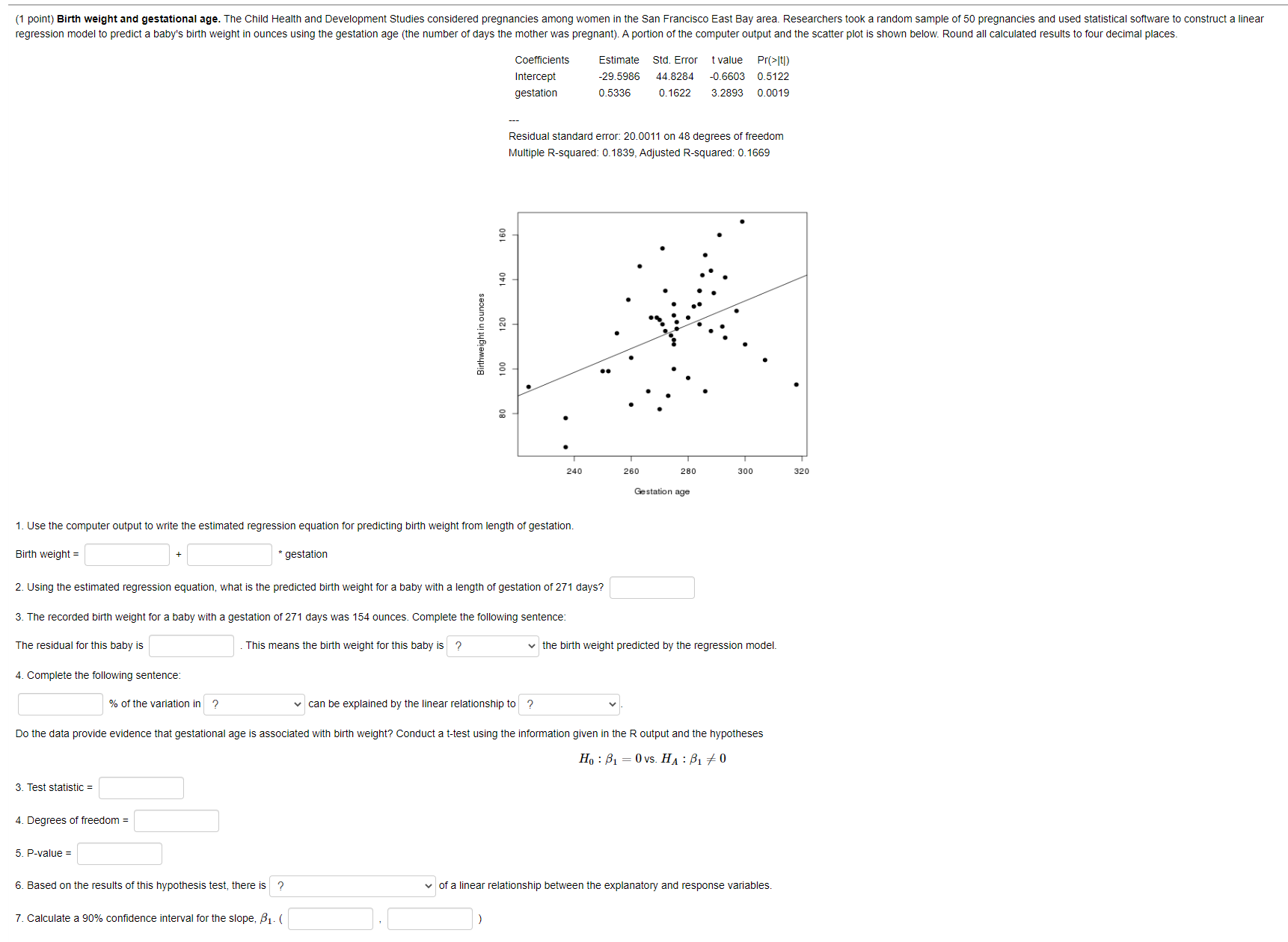
ExtraCredit-09: Problem 2 Problem Value: 1 point(s). Problem Score: 62%. Attempts Remaining: Unlimited. (1 point) Honeybee colonies ~ From 1995 to 2012, researchers surveyed the number of honeybee colonies in order to determine whether the population changed over time. The scatterplot below shows the relationship between these two variables along with the least squares fit. Round all calculated results to 4 decimal places unless otherwise indicated. Honeybee Colonies 2700 2600 2500 Colonies 2400 2300 1995 2000 2005 2010 Year 1. The relationship between year and number of honeybee colonies is negative , weak , and linear 2. The explanatory variable is year and the response variable is number of bee colonies The summary statistics for number of colonies and year are listed below. The correlation between number of colonies and year is r = -0.4098. Year: mean = 2003.5, standard deviation = 5.3385 Colonies: mean = 2546.0556, standard deviation = 109 3. Calculate the equation for the regression line. Remember not to round for intermediate calculations. Round only your final results to 6 decimal places. y = 4.Complete the following sentence to interpret the slope of the regression line: As the year increases by 1, there is an associated decrease | in the number of colonies of on average. 5. Use the regression equation to estimate the number of colonies in 1996 y 1996 = 6. The actual number of colonies in 1996 was 2566. Complete the following sentence. The residual for 1996 is This means the number of colonies in 1996 isExtraCredit-09: Problem 3 Problem Value: 1 point(s). Problem Score: 0%. Attempts Remaining: Unlimited. (1 point) College Graduation Rates. Data from the College Results Online website compared the 2011 graduation rate and median SAT score for 92 similar-sized public universities and colleges in the United States. The scatterplot below shows the relationship between these two variables along with the least squares fit. Round all calculated results to 4 decimal places. Graduation Rate by Median SAT 90 80 70 60 Graduation Rate 40 50 30 900 1000 1 100 1200 1300 Median SAT 1. The relationship between median SAT score and graduation rate is ? v . ? v, and ? 2. The explanatory variable is ? and the response variable is ? The summary statistics for graduation rate and median SAT score are listed below. The correlation between graduation rate and median SAT score is 0.659. Median SAT score: mean = 1031.1, standard deviation = 80.4 Graduation rate: mean = 51.2, standard deviation = 13.9 3. The equation of the regression line is y = 4. Complete the following sentence to interpret the slope of the regression line: An increase of in Median SAT score corresponds to a/an ? of in Graduation Rate. 6. The recorded median SAT score for Northern Michigan University is 1034. Use the regression equation to estimate the graduation rate for Northern Michigan University. 6. The recorded graduation rate for Northern Michigan University is 47.5. Complete the following sentence. The residual for Northern Michigan University is This means the graduation rate at Northern Michigan University isExtraCredit-09: Problem 4 Problem Value: 1 point(s). Problem Score: 0%. Attempts Remaining: Unlimited. (1 point) College Graduation Rates. Data from the College Results Online website compared the 2011 graduation rate and school size for 92 similar-sized public universities and colleges in the United States. Statistical software was used to create the linear regression model using size as the explanatory variable and graduation rate as the response variable. Summary output from the software and the scatter plot are shown below. Round all calculated results to four decimal places. Coefficients Estimate Std. Error t value Pr(>It1) Intercept 41.442572 4.427554 9.36 6.1e-15 Size 0.001051 0.000481 2.18 0.031 Residual standard error: 13.1 on 90 degrees of freedom Multiple R-squared: 0.0504, Adjusted R-squared: 0.0398 F-statistic: 4.77 on 1 and 90 DF, p-value: 0.031 Graduation Rate by Size 8 80 70 60 Graduation rate 50 40 GOOD 8000 10000 12000 14000 Size of School 1. Write the equation for the regression line for predicting graduation rate from the size of the school. Grad Rate = (Size) 2. Complete the following sentence: % of the variation in ? can be explained by the linear relationship to ? Do the data provide strong evidence (or = 0.05) that the size of the school is associated with the graduation rate? Conduct a t-test using the information given in the R output and the hypotheses Ho : B1 = Ovs. HA : B1 #0 Use a = 0.05 3. Test statistic = 4. Degrees of freedom = 5. P-value = 6. Based on the results of this hypothesis test, there ? a significant linear relationship between the explanatory and response variables. 7. Calculate a 95% confidence interval for the slope, B1- ((1 point) Birth weight and gestational age. The Child Health and Development Studies considered pregnancies among women in the San Francisco East Bay area. Researchers took a random sample of 50 pregnancies and used statistical software to construct a linear regression model to predict a baby's birth weight in ounces using the gestation age (the number of days the mother was pregnant). A portion of the computer output and the scatter plot is shown below. Round all calculated results to four decimal places. Coefficients Estimate Std. Error t value Pr(>[t) Intercept 29.5986 44.8284 -0.6603 0.5122 gestation 0.5336 0.1622 3.2893 0.0019 Residual standard error: 20.0011 on 48 degrees of freedom Multiple R-squared: 0.1839, Adjusted R-squared: 0. 1669 160 140 120 Birthweight in ounces 100 240 260 280 300 320 Gestation age 1. Use the computer output to write the estimated regression equation for predicting birth weight from length of gestation. Birth weight = gestation 2. Using the estimated regression equation, what is the predicted birth weight for a baby with a length of gestation of 271 days? 3. The recorded birth weight for a baby with a gestation of 271 days was 154 ounces. Complete the following sentence: The residual for this baby is This means the birth weight for this baby is ? the birth weight predicted by the regression model. 4. Complete the following sentence. % of the variation in ? can be explained by the linear relationship to ? Do the data provide evidence that gestational age is associated with birth weight? Conduct a t-test using the information given in the R output and the hypotheses Ho : B1 = Ovs. HA : B1 #0 3. Test statistic = 4. Degrees of freedom = 5. P-value = 6. Based on the results of this hypothesis test, there is ? of a linear relationship between the explanatory and response variables. 7. Calculate a 90% confidence interval for the slope, B1 - (ExtraCredit-08: Problem 8 Problem Value: 1 point(s). Problem Score: 0%. Attempts Remaining: Unlimited. (1 point) Grand Slam ~ An ESPN reporter wants to use statistical inference to determine if the average viewership of Wimbledon finals is higher than the French Open finals. He randomly selects a sample of 31 Wimbledon finals and 32 French Open finals. The summary statistics are given in the table below in millions of viewers. Grand Slam Mean Number of Viewers Standard Deviation Population 1: Wimbledon 21.52 1.636 Population 2: French Open 20.83 3.901 1. Which type of inference procedure should be used? O A. Two sample t-test for the difference in independent means O B. One sample t-interval for a population mean O C. Two sample Z-test for the difference in population proportions O D. Chi-square test of independence O E. Chi-square goodness of fit test 2. Express the research question in terms of a null and an alternative hypothesis. OA. Ho : /1 = 12 VS. Ha : M1 # #2 OB. Ho : /1 = 12 VS. Ha : #1 > /2 OC. Ho : /1 = 12 VS. Ha : 1