F# ASSIGNMENT

Problem 1 Given vectors u = (u1, u2 ,..., un) and v = (v1, v2 ,..., vn), the inner product of u and v is defined to be u1*v1 + u2*v2 + ... + un*vn.

Write a curried F# function inner that takes two vectors represented as int lists and returns their inner product (assuming the two lists are of equal length):

> inner [1;2;3] [4;5;6];;

val it : int = 32

Problem 2 Given an m-by-n matrix A and an n-by-k matrix B, the product of A and B is an m-by-k matrix whose entry in position (i,j) is the inner product of row i of A with column j of B. For example,

=

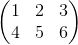
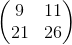
Write an uncurried F# function to do matrix multiplication (assuming the dimensions of two given matrices are appropriate):

> multiply ([[1;2;3];[4;5;6]], [[0;1];[3;2];[1;2]]);;

val it : int list list = [[9; 11]; [21; 26]]

Hint: Use transpose (from previous assignment), inner, and List.map.

Problem 3 Write mergesort in F#:

A merge sort works as follows recursively:

(1) Divide the unsorted list into two sublists;

(2) Sort the two sublists;

(3) Merge two sorted sublists to produce a new sorted list.

Use the split function in Homework #3 to accomplish step (1);

Write a recursive function merge to merge to sorted sublists into one sorted list to do (3);

Write a recursive function mergesort, which uses the split function to obtain two unsorted sublists from one unsorted list, recursively calls itself on the two unsorted sublists, and then uses merge to get the final sorted list.

Problem 4 Write an F# program to evaluate arithmetic expressions written in the language given by the following context-free grammar:

E -> n | -E | E + E | E - E | E * E | E / E | (E)

In the above, n is an integer literal, -E is the negation of E, the next four terms are the sum, difference, product, and quotient of expressions, and (E) is used to control the order of evaluation of expressions, as in the expression 3*(5-1).

(1) Use F# type definition (discriminated union type) to define an abstract syntax tree grammar based on the above concrete grammar by completing the following partial solution:

type Exp = Num of int| Prod of Exp * Exp | ...

(hint: add one constructor in the discriminated union type for each rule. No constructor is needed for the parentheses rule). The example given above would simply be represented by

2

Prod(Num 3, Diff(Num 5, Num 1)).

(2) To deal with possible division by zero, we make use of the built-in F# type in our evaluate function:

type 'a option = None | Some of 'a

evaluate returns Some n in the case of a successful evaluation, and None in the case of an evaluation that fails due to dividing by zero. For example,

> evaluate (Prod(Num 3, Diff(Num 5, Num 1)));;

val it : int option = Some 12

> evaluate (Diff(Num 3, Quot(Num 5, Prod(Num 7, Num 0))));;

val it : int option = None

(3) Write a recursive function evaluate to evaluate arithmetic expressions defined using the type definitions in (1) & (2). evaluate e should use pattern matching based on the discriminated union type to evaluate each of e's sub-expressions; it should also distinguish between the cases of successful or failed sub-evaluations. To get you started, here is the beginning of the definition of evaluate:

let rec evaluate = function

| Num n -> Some n

| Neg e -> match evaluate e with

| Some n -> Some (-n)

| None -> None

| Sum (e1, e2) -> match (evaluate e1, evaluate e2) with

|...

| ...

Problem 5 Describe two features of F# that you have difficult to understand and use.

36 25 14