Answered step by step
Verified Expert Solution
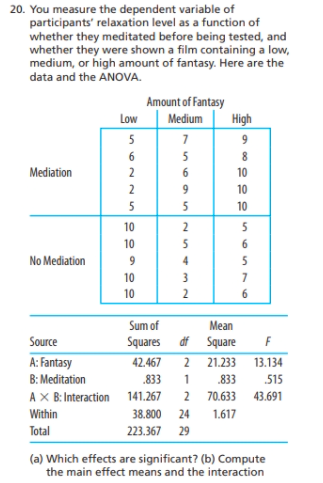
Question
1 Approved Answer
f16. Felix measured participants' preferences for two brands of soft drinks (factor A). For each brand he tested male and female participants (factor B). The




Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


