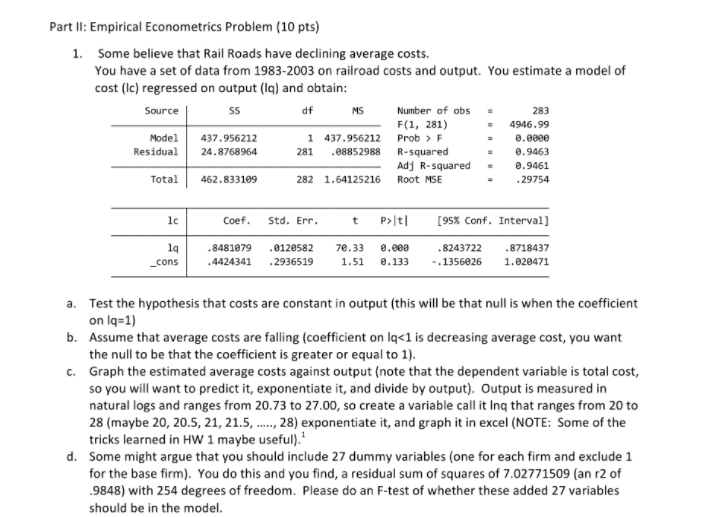
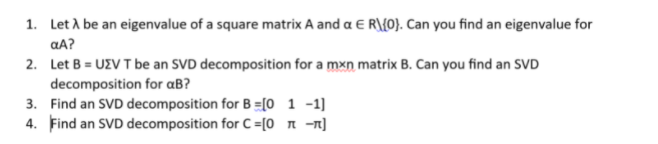EXERCISE 4.36. In Example 4.20, use Eq. 4.16 to verify that the fake spheres with a = 2 and a = , have no umbilical points. (4.16) T. EXAMPLE 4.20 (Fake Spheres). We wish to construct surfaces of revolution with constant Gaussian curvature equal to 1. If K = 1, then Eq. 4.15 says that x" = -x. The following is a solution for every a > 0: (4.17) x(t) = a cos(t). The hypothesis that y is parametrizationgth, so (x')2 + (2')2 = 1, means that z is determined by x as follows: (4.18) = (t) = VI - x'(s)2 ds = 1 - a2 sin? (s) ds. (4.15) K1. Consider the simple regression model: V/i = Po+ Piri +ui, for i = 1, ..., n, with E(ur,) 7 0 and let z be a dummy instrumental variable for a, such that we can write: with E(uilz;) = 0 and E(vilzi) = 0. (c) Denote by no, the number of observations for which z =0 and by n, the number of observations for which z, = 1. Show that: (a - 2) = =(n-m). 1=1 and that: [(8 -=)(3: - 9) = 7 "(n - ni) (31 - 90) . where to and g are the sample means of y for z equal to 0 and 1 respectively. (Hint: Use the fact that n = nj + no, and that = = m). (d) Now we regress y on i to obtain an estimator of 81. From the standard formula of the slope estimator for an OLS regression and using the result in (c), show that: By1 - 90 I1 - To This estimator is called the Wald estimator.\f(3) Consider an exchange economy with two consumers. Consumer A has utility function U(X1, 12) = $1 + 12 and endowment wA = (60, 10). Consumer B has utility function UB($1, 12) = 1142 and endowment w = (20, 30). (a) Draw wn Edgeworth box with the initial endowment and the correspond indifference curves through the endowment for consumer A and consumer B. (b) Note that at any Pareto efficient allocation where both consumers get strictly positive amounts of each good, their MRS must be the same. Use this observation to construct the contract curve. Are there Pareto effcient point where consumer A does not get a strictly positive allocation of both goods.? Draw the contract curve in the Edgeworth box. (c) Find the competitive equilibrium prices and competitive allocation. (d) Now consider an economy with 1000 consumers identical to consumer A and 1000 con- sumers identical to consumer B. That is each consumer A has the same initial endowment and utility functon, and similarly, each consumer B has the same endowment and utility function. Find a competitive equilibrium of the economy with 2000 consumers.(3) Consider an exchange economy with two consumers. Consumer A has utility function U($1, 12) = x1 + 12 and endowment we = (60, 10). Consumer B has utility function UB($1, 12) = $142 and endowment w = (20, 30). (a) Draw wn Edgeworth box with the initial endowment and the correspond indifference curves through the endowment for consumer A and consumer B. (b) Note that at any Pareto efficient allocation where both consumers get strictly positive amounts of each good, their MRS must be the same. Use this observation to construct the contract curve. Are there Pareto effcient point where consumer A does not get a strictly positive allocation of both goods.? Draw the contract curve in the Edgeworth box. (c) Find the competitive equilibrium prices and competitive allocation. (d) Now consider an economy with 1000 consumers identical to consumer A and 1000 con- sumers identical to consumer B. That is each consumer A has the same initial endowment and utility functon, and similarly, each consumer B has the same endowment and utility function. Find a competitive equilibrium of the economy with 2000 consumers