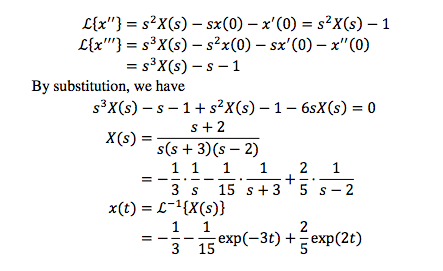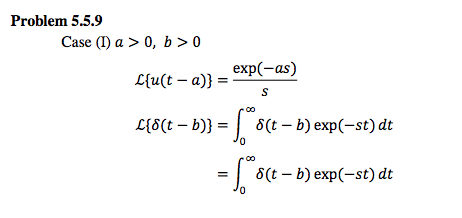\f\f\f\f\f= elm-ks) Applying Laplace to both sides of the equaon 521.15) 51(0) 010 + 2(sX(s) 15(0)) + 1((3) = eXPK-HS) + exp( b5) Substitute 1C. sms) + 2mg) + m) = \"pt\"5) + expE-bs) m3 = \"(E"3) + \"PE-b5) = mils; + exptbs) n+3: 3+1? n+1? x(:) = L-1{X(s)} =Ltsinm\"m+rn:n*\"\"m = L_1{"p(_'\") @- \"L1 _ [s :1? Wm} = u[t a){u[t a) exp[-(t 5)) - (t - a) exn[-[t -b))} + u(t b)(t b) exp((t 5)] = uEt a)[1 exp([t 11)) [t a) exp[(t 110] + u(: b)(t 11) exp((: 11)) Case(]])as,b>0 1 L{u(t - (1)} = E 3m: b)] = exp(bs) Applying Laplace In both sides of the equation 1 SEATS) + 2511(5) + 3(3) = E + expEbs) apt-b5) 5(5 + 1)2 + (s + 1)2 _ _ 1_i_ 1 _ expEhs) \"n'lk 5+1 n+nJ+Liin+nz} X(s) = = utt) - exp(-t) - t exp(-t) + at: b)[t b) exp((t 5)) = 1 - exp(-t) - t exv(t) + utt b)[t b) exp((t 5)) Problem 5.5.10 Take laplace on each side of both equations. Lix'} = Alix} + 2M] {y'} = nix} - 250} Given I.C., this gives [[5 1)X(s) = 2Y(s) + 1 2XEs) (s + 2)Y(s) This gives x{)1 1 +3 1 [S '5' + 5' 2 1 + Finally 5 _ Ztexpt2t) exp(3r)) 10): 4 exp(2t) + exp(-3t) ytt) 5 \fPrnblem 5.5.11 {HIT} = '2L{x1}+ Lira} + exPP\") ME] = Lin} L132} + expter) {3213 (S) = -2X1(S) + 12(3) + allot-TS) 5232(5) = 31(5) X28) + Elli275) {132(3) = [52 + 2)X1(S)- eXP'Z-TS) (s2 + BK; (s) = X18) + arm2:5) Insert rst equation into second. {32 + HUS: + 23X1(S) rm75)) = X15) + Elli2\") (3\" + 352 + 1)X1(s) = exp(Is) (exp(-rs) + $2 + 1) exp(rs) [exp('rs) + s2 + 1) (33+3-l-2'/)(s2 +3 E'G) elm-TS) 3+ 5 3 5 2 2 (s 2W\" 2\"? x1 {0 = 131 = n(t T)_1 Using partial fracnns we nd 1 B 3 ($2 +3+2J)(52+32 Where 1 D= 5 and 32+1 _ F + H 3+ 5 3 5 _ 3+J 3(5 2 2 2 2. ( + 200+ 2f) + 2 + 2 where 1+J F: NE and 5-1 25 Then We also have {52 + 1mm = X1 (5) + exp(- Z'rs) \fL'1{I[s]} = sin net 3121 3 ram-11:1 + 2 = 3 sin :11: E EKp(-2l'} 2 sin {MEI exp[r} Prelileni 5.5.13 By applying lsplsee trensferm be given a system DE DE, we get fellewing. I'D?) = 21::(1) + t) + 1 '[ = IE} + 23(3) + 3311(3) 31111331 IN) = 23(3) + i'[s) + 31: 1 [9H 2)+ 3 1 x s s I\" 3': [3-1}[33)+ see-11:34) rm} 1 +[3 - 1] [s 3+ [3 - 1]1(3 - 3} 1"[s)- _ 1(1)} 1 (3-1][s3]+ 33(31](33) +F[)(5 - 2J+ [3 3) +(3 - 1}[s 3]+ [s- 1}3{3 - 3] We need partial freetiens fer each term in the shave DEs. xt) [3 - 2) xiig 1 1 [s1][3-3) 21+s-sll 3-2 s 211 1 32(31)(s-s}=__ Tying-131+ 13[s-3} &_ 1 + 1 3, [s1)(33) 2 31 33 1 1 1 [s 13,2[3 - 3} 4(3 1) 2(3 1)2 +43 s) \f\f\fre: = #1 l\"rt-11(3) + 2 exPE-t) Then we can have the RS. like the fellewhtg fe'n em = 113:3 + All: +Aa xp = 231:: + A1 IQ}: = 2A: Substitute inte the erig'mel equetien. 2.41 2(2111: +441] - 3.32:3 + A1: + Ac.) = r1 + 4: Then 38 15 1 A =,A =-,A = \" 2? 1 e 2 3 SetheG.S.ie 1 15 35 _ _ _ E__ _ xgelexp(3t)+egexp[ t}+3t 9 \"-2? r 2 15 I: = 3E1 unt) - E1 apt-t) + gt - 3 Suhatituteinte _1'1rI2tl 1'1 2 Weeenhave 2 11 43 _ _ _ __3 _ __ IlElp(3t) EEEIPE t} 3t +9: 2? St:- the selutien is 2 11 43 _ _ _ __1 _ __ xlelexpt] C2EIP[ t] 3: +9: 2? 1 15 35 _ _ _ E__ _ xgelexp(3t)+egexp[ t}+3t 9 \"-2? Prehlem 1.15 434 I = I\" = y' = 9x+5x' x"x'+9x= r25r+9= r1=r1=3 Hence: In) = [A + 3:) expt} 3.1:) = [3A + H + 33:] expt} Prnhlem 4.3.1 Jr." = 1' .. 2]! [1) [1W = I -* 1* (21' Pm Eq-El) x = 1:" + J? 1" = y" + 11' Hugging this intn Eq-[l) 1' = Jr: -- 2}! 1'\" H" =1r'+.v\"2.v J?\" + r = TheC-Eqis r1 + 1 = :1 TL: = ii t] = E1 cust+ E2 sint Puttls back, and t] = (E; - E1] sin: + [1 + 2} ms: Hugging in the 1.11, we have 1=+ 2= [2'1 = 2 [E1 = 1 Thus t) = trust .. 35in: [t]! = Ems: +- sin: Prehlem 5.5.3 Take lsplsee run each side ef twe DEs, we have HI" = -4.E{I} + L{sin t} m = 4m} ace: let HI} = Js). We lmew that L{x\"} = s31 (s) - x[)s I'm) Plugging ihte the rst DE we get 2 _ = s IEs) HE'S IT\") 43(3) + 32 + 1 This gives m) = W [s2 + 4-)[33 + 1) Thus, the (3.5. ef t) is t) = L'1{I[s}}. Similarly, fer _v, let Lbs] = 113]}. This gives L{_v\"} = sts) ytms - 3:10) The seeehd DE can he w1itten ss szs} Jr[)s 3.9m] = 43(3) - HHS) This gives 4H3) + 229303 + .v'ti s2 + B Hugging 3(3) ihte the shave equetieh, we can get his} in terms efs, then the GS. e1\" _v[t) is: t] = L'1[F[s)] rm = Prehlem 5.5.4 Take lsplsee e11 each side at\" the equetien, we have L{x'"} + L{:t'\"} L{x'} = LetL{x} = JETS]. then Hf} = 3.151(3) - rm} = sX[s) PrnhlI- 5.5.tl Take laplace m1 each side (11' the: aquan, we. have L-[xm] + L[:r:\"} L{x'} = Letx} = I [3). than L{x'} = 3.1" [3) ... 1\"\" = 31$) \f\f