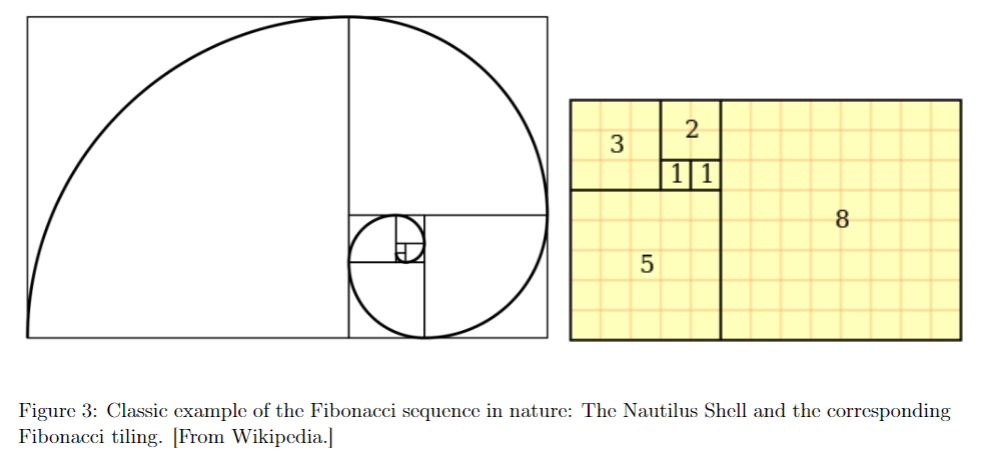
Fibonacci numbers appear in nature and art and in classical theories of beauty and proportion. The Fibonacci sequence is defined as F Fn1 + n-2. That is, any number in the sequence is the sum of = the previous two numbers. The fifth Fibonacci number is the sum of the fourth and the third Fibonacci numbers. The fourth number is the sum of the third and the second. The first Fibonacci number is 0 and the second, 1. 1. (8 points) Computing and analyzing Fibonacci numbers. The following table gives the first ten Fibonacci numbers (if starting at 0). Position in the sequence Fibonacci Number 0 0 1 1 2 1 3 2 4 3 5 5 6 8 7 13 8 21 9 10 34 55 Turn in a table with 50 rows and 4 columns. In the first column, called Position, list the position of each Fibonacci number. In column 2, called Fibonacci Number, list the Fibonacci numbers. In column 3, called Approximation, show the quotient of two consecutive Fibonacci numbers. In column 4, called Quality of Approximation, show the difference between a quotient and the Golden Ratio. Put the Golden Ratio into a cell named GoldenRatio (=(SQRT(5)+1)/2), i.c., 1.618 ...). In the future, we will write a formula that produces the first k Fibonacci numbers within the limits of Excel and your device. Above, we did it manually for k=50. 2. (4 points) Informally discuss, based on the data, that for large n, the ratio of consecutive Fibonacci numbers approaches (but never reaches for finite n) the Golden Ratio. 3. (8 points) Visualizing the Fibonacci sequence using Stacking of Building Blocks. A Fibonacci spiral approximates the golden spiral using quarter-circle arcs inscribed in squares derived from the Fibonacci sequence (from Wikipedia). We only focus on the squares and don't show the arcs. Check Fig. in Appendix B. Run this formula in a cell of your worksheet that has enough free cells down and to the right. 3. (8 points) Visualizing the Fibonacci sequence using Stacking of Building Blocks. A Fibonacci spiral approximates the golden spiral using quarter-circle arcs inscribed in squares derived from the Fibonacci sequence (from Wikipedia). We only focus on the squares and don't show the arcs. Check Fig. 3 in Appendix B. Run this formula in a cell of your worksheet that has enough free cells down and to the right. VSTACK( HSTACK (SEQUENCE (3,3,3,0), VSTACK (SEQUENCE (2,2,2,0), HSTACK (SEQUENCE (1,1,1,0), SEQUENCE (1,1,1,0)))), SEQUENCE (5,5,5,0)) You will recognize a part of the Fibonacci spiral for the partial Fibonacci sequence 1,1,2,3,5. Extend the Fibonacci spiral by adding the next Fibonacci number 8. Modify the formula accordingly and turn in your modified formula. As in Kindergarten, we have two stacking operations for our building blocks which are squares: With VSTACK we can vertically stack them, and with HSTACK we can horizontally stack them. The repeated use of the SEQUENCE function creates the building blocks, the squares. 2 3 11 8 5 Figure 3: Classic example of the Fibonacci sequence in nature: The Nautilus Shell and the corresponding Fibonacci tiling. [From Wikipedia.]