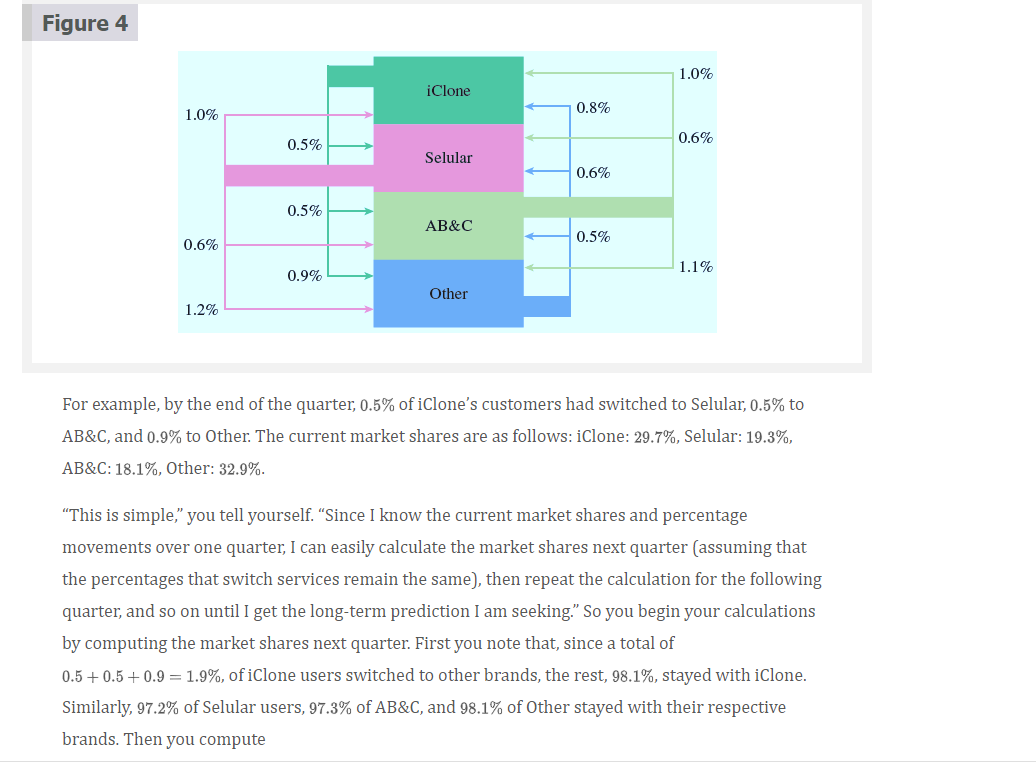
Figure 4 1.0% iClone 1.0% 0.8% 0.5% 0.6% Selular 0.6% 0.5% AB&C 0.5% 0.6% 1.1% 0.9% Other 1.2% For example, by the end of the quarter, 0.5% of iClone's customers had switched to Selular, 0.5% to AB&C, and 0.9% to Other. The current market shares are as follows: iClone: 29.7%, Selular: 19.3%, AB&C: 18.1%, Other: 32.9%. This is simple, you tell yourself. Since I know the current market shares and percentage movements over one quarter, I can easily calculate the market shares next quarter (assuming that the percentages that switch services remain the same), then repeat the calculation for the following quarter, and so on until I get the long-term prediction I am seeking." So you begin your calculations by computing the market shares next quarter. First you note that, since a total of 0.5 +0.5 +0.9 = 1.9%, of iClone users switched to other brands, the rest, 98.1%, stayed with iClone. Similarly, 97.2% of Selular users, 97.3% of AB&C, and 98.1% of Other stayed with their respective brands. Then you compute Similarly, 97.2% of Selular users, 97.3% of AB&C, and 98.1% of other stayed with their respective brands. Then you compute iClone share after one quarter = 98.1% of iClone + 1.0% of Selular + 1.0% of AB&C +0.8% of Other = (0.981)(0.297) + (0.010) (0.193) + (0.010) (0.181) + (0.008)(0.329) = 0.297729, or 29.7729%. Similarly, Selular share: (0.005)(0.297) + (0.972)(0.193) + (0.006) (0.181) + (0.006) (0.329) = 0.192141 AB&C share: (0.005) (0.297) + (0.006) (0.193) + (0.973)(0.181) + (0.005) (0.329) 0.180401 Other share: (0.009) (0.297) + (0.012) (0.193) + (0.011)(0.181) + (0.981)(0.329) = 0.329729. So you project the market shares after one quarter to be iClone: 29.7729%, Selular: 19.2141%, AB&C: 18.0401%, Other: 32.9729%. You now begin to realize that repeating this kind of calculation for the large number of quarters required for long-term projections will be tedious. You call in your student large number of quarters required for long-term projections will be tedious. You call in your student intern (who happens to be a mathematics major) to find out whether she can help. After taking one look at the calculations, she makes the observation that all you have really done is compute the product of two matrices: [0.297729 0.192141 0.180401 0.329729] 6.981 .005 .005 .009 .010 .972 .006 .012 = [0.297 0.193 0.181 0.329] .010 .006 973 .011 .008 .006 .005 .981 Market shares after one quarter = Market shares at start of quarter * A. The 4 x 4 matrix A is organized as follows: To: iClone Selular AB&C Other iClone.981 .005 .005 .009 Selular .010 972 .006 .012 AB&C .010 .006 973 .011 Other 1.008 .006 .005 981 From: Since the market shares one quarter later can be obtained from the shares at the start of the quarter, you realize that you can now obtain the shares two quarters later by multiplying the result by A, and at this point, you start using technology (such as the Matrix Algebra Tool at www.WanerMath.com) to continue the calculation: Market shares after two quarters = Market shares after one quarter A .981 .005 .005 .009 .010 .972 006 .012 = [0.297729 0.192141 0.180401 0.329729] .010 .006 .973 .011 1.008 .006 .005 .981 [0.298435 0.191310 0.179820 0.330434] . Although the use of matrices has simplified your work, multiplying the result by A over and over again to get the market shares for successive months is still tedious. Would it not be possible to get, say, the market share after 10 years (40 quarters) with a single calculation? To explore this, you decide to use symbols for the various market shares: mo = Starting market shares = [0.297 0.193 0.181 0.329] mi = Market shares after 1 quarter [0.297729 0.192141 0.180401 0.329729] m2 = Market shares after 2 quarters : mp = Market share after n quarters. You then rewrite the relationships above as m1 = moA Shares after one quarter = Shares at start of quarter x A Shares after two quarters = Shares after one quarter x A. m2 = mA On an impulse, you substitute the first equation in the second: m2 = m; A = (moA) A = mo A. Continuing, you get mg = m2 A = (mA2) A = mo A3 my moA", which is exactly the formula you need! You can now obtain the 2-, 5-, and 10-year projections each in a single step (with the aid of technology): 2-year projection: mg = mo AS 8 1.981 .005 .005 .009 .010 .972.006 .012 = [0.297 0.193 0.181 0.329] .010 .006 973 .011 1.008 .006 .005 .981 [0.302237 0.186875 0.176691 0.334198] 5-year projection: M20 = mo A20 [0.307992 0.180290 0.171938 0.33978] 10-year projection: M40 = mo 440 [0.313857 0.1738090.167074 0.34526]. In particular, Selular's market shares are projected to decline slightly: 2-year projection: 18.7%, In particular, Selular's market shares are projected to decline slightly: 2-year projection: 18.7%, 5-year projection: 18.0%, 10-year projection: 17.4%. You now move on to the worst-case scenario, which you represent by assuming 100% loyalty by iClone users with the remaining percentages staying the same (Figure 5). Figure 5 1.0% iClone 1.0% 0.8% 0.6% 0% Selular 0.6% 0% AB&C 0.6% 0.5% 1.1% 0% Other 1.2% 1 0 0 0 The matrix A corresponding to this diagram is .010 .972.006 .012 , and you find .010 .006 .973 .011 .008 .006 .005 981 2-year projection: mg = my A8 (0.346335 0.175352 0.165200 0.313113] 5-year projection: m20 = mo A20 [0.413747 0.152940 0.144776 0.288536] 10-year projection: M40 = mo A10 = [0.510719 0.123553 0.117449 0.248279). 5-year projection: m20 = mo A20 [0.413747 0.152940 0.144776 0.288536] 10-year projection: M40 = mo 410 [0.510719 0.123553 0.117449 0.248279]. Thus, in the worst-case scenario, Selular's market shares are projected to decline more rapidly: 2-year projection: 17.5%, 5-year projection: 15.3%, 10-year projection: 12.4%. Exercises 1. Project Selular's market share 20 and 30 years from now based on the original data shown in Figure 4. (Round all figures to the nearest 0.1%.) 2. Using the original data, what can you say about each company's share in 60 and 80 years (assuming that current trends continue)? (Round all figures to the nearest 0.1%.) 3. Obtain a sequence of projections several hundreds of years into the future using the scenarios in both Figure 4 and Figure 5. What do you notice? 4. Compute a sequence of larger and larger powers of the matrix A for both scenarios with all figures rounded to four decimal places. What do you notice? Figure 4 1.0% iClone 1.0% 0.8% 0.5% 0.6% Selular 0.6% 0.5% AB&C 0.5% 0.6% 1.1% 0.9% Other 1.2% For example, by the end of the quarter, 0.5% of iClone's customers had switched to Selular, 0.5% to AB&C, and 0.9% to Other. The current market shares are as follows: iClone: 29.7%, Selular: 19.3%, AB&C: 18.1%, Other: 32.9%. This is simple, you tell yourself. Since I know the current market shares and percentage movements over one quarter, I can easily calculate the market shares next quarter (assuming that the percentages that switch services remain the same), then repeat the calculation for the following quarter, and so on until I get the long-term prediction I am seeking." So you begin your calculations by computing the market shares next quarter. First you note that, since a total of 0.5 +0.5 +0.9 = 1.9%, of iClone users switched to other brands, the rest, 98.1%, stayed with iClone. Similarly, 97.2% of Selular users, 97.3% of AB&C, and 98.1% of Other stayed with their respective brands. Then you compute Similarly, 97.2% of Selular users, 97.3% of AB&C, and 98.1% of other stayed with their respective brands. Then you compute iClone share after one quarter = 98.1% of iClone + 1.0% of Selular + 1.0% of AB&C +0.8% of Other = (0.981)(0.297) + (0.010) (0.193) + (0.010) (0.181) + (0.008)(0.329) = 0.297729, or 29.7729%. Similarly, Selular share: (0.005)(0.297) + (0.972)(0.193) + (0.006) (0.181) + (0.006) (0.329) = 0.192141 AB&C share: (0.005) (0.297) + (0.006) (0.193) + (0.973)(0.181) + (0.005) (0.329) 0.180401 Other share: (0.009) (0.297) + (0.012) (0.193) + (0.011)(0.181) + (0.981)(0.329) = 0.329729. So you project the market shares after one quarter to be iClone: 29.7729%, Selular: 19.2141%, AB&C: 18.0401%, Other: 32.9729%. You now begin to realize that repeating this kind of calculation for the large number of quarters required for long-term projections will be tedious. You call in your student large number of quarters required for long-term projections will be tedious. You call in your student intern (who happens to be a mathematics major) to find out whether she can help. After taking one look at the calculations, she makes the observation that all you have really done is compute the product of two matrices: [0.297729 0.192141 0.180401 0.329729] 6.981 .005 .005 .009 .010 .972 .006 .012 = [0.297 0.193 0.181 0.329] .010 .006 973 .011 .008 .006 .005 .981 Market shares after one quarter = Market shares at start of quarter * A. The 4 x 4 matrix A is organized as follows: To: iClone Selular AB&C Other iClone.981 .005 .005 .009 Selular .010 972 .006 .012 AB&C .010 .006 973 .011 Other 1.008 .006 .005 981 From: Since the market shares one quarter later can be obtained from the shares at the start of the quarter, you realize that you can now obtain the shares two quarters later by multiplying the result by A, and at this point, you start using technology (such as the Matrix Algebra Tool at www.WanerMath.com) to continue the calculation: Market shares after two quarters = Market shares after one quarter A .981 .005 .005 .009 .010 .972 006 .012 = [0.297729 0.192141 0.180401 0.329729] .010 .006 .973 .011 1.008 .006 .005 .981 [0.298435 0.191310 0.179820 0.330434] . Although the use of matrices has simplified your work, multiplying the result by A over and over again to get the market shares for successive months is still tedious. Would it not be possible to get, say, the market share after 10 years (40 quarters) with a single calculation? To explore this, you decide to use symbols for the various market shares: mo = Starting market shares = [0.297 0.193 0.181 0.329] mi = Market shares after 1 quarter [0.297729 0.192141 0.180401 0.329729] m2 = Market shares after 2 quarters : mp = Market share after n quarters. You then rewrite the relationships above as m1 = moA Shares after one quarter = Shares at start of quarter x A Shares after two quarters = Shares after one quarter x A. m2 = mA On an impulse, you substitute the first equation in the second: m2 = m; A = (moA) A = mo A. Continuing, you get mg = m2 A = (mA2) A = mo A3 my moA", which is exactly the formula you need! You can now obtain the 2-, 5-, and 10-year projections each in a single step (with the aid of technology): 2-year projection: mg = mo AS 8 1.981 .005 .005 .009 .010 .972.006 .012 = [0.297 0.193 0.181 0.329] .010 .006 973 .011 1.008 .006 .005 .981 [0.302237 0.186875 0.176691 0.334198] 5-year projection: M20 = mo A20 [0.307992 0.180290 0.171938 0.33978] 10-year projection: M40 = mo 440 [0.313857 0.1738090.167074 0.34526]. In particular, Selular's market shares are projected to decline slightly: 2-year projection: 18.7%, In particular, Selular's market shares are projected to decline slightly: 2-year projection: 18.7%, 5-year projection: 18.0%, 10-year projection: 17.4%. You now move on to the worst-case scenario, which you represent by assuming 100% loyalty by iClone users with the remaining percentages staying the same (Figure 5). Figure 5 1.0% iClone 1.0% 0.8% 0.6% 0% Selular 0.6% 0% AB&C 0.6% 0.5% 1.1% 0% Other 1.2% 1 0 0 0 The matrix A corresponding to this diagram is .010 .972.006 .012 , and you find .010 .006 .973 .011 .008 .006 .005 981 2-year projection: mg = my A8 (0.346335 0.175352 0.165200 0.313113] 5-year projection: m20 = mo A20 [0.413747 0.152940 0.144776 0.288536] 10-year projection: M40 = mo A10 = [0.510719 0.123553 0.117449 0.248279). 5-year projection: m20 = mo A20 [0.413747 0.152940 0.144776 0.288536] 10-year projection: M40 = mo 410 [0.510719 0.123553 0.117449 0.248279]. Thus, in the worst-case scenario, Selular's market shares are projected to decline more rapidly: 2-year projection: 17.5%, 5-year projection: 15.3%, 10-year projection: 12.4%. Exercises 1. Project Selular's market share 20 and 30 years from now based on the original data shown in Figure 4. (Round all figures to the nearest 0.1%.) 2. Using the original data, what can you say about each company's share in 60 and 80 years (assuming that current trends continue)? (Round all figures to the nearest 0.1%.) 3. Obtain a sequence of projections several hundreds of years into the future using the scenarios in both Figure 4 and Figure 5. What do you notice? 4. Compute a sequence of larger and larger powers of the matrix A for both scenarios with all figures rounded to four decimal places. What do you notice