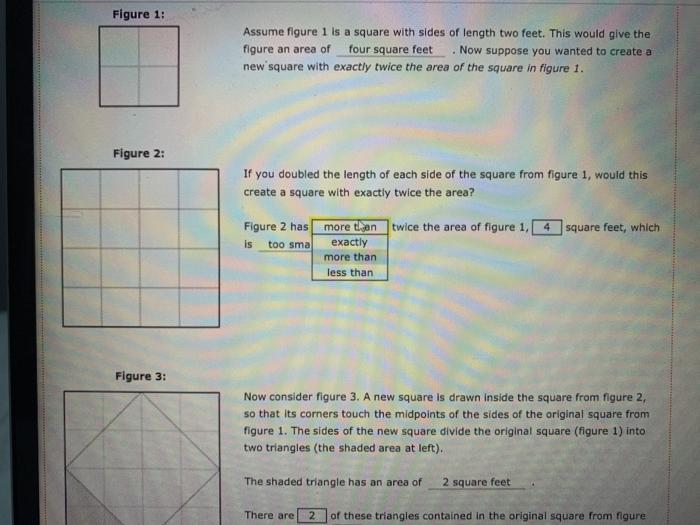
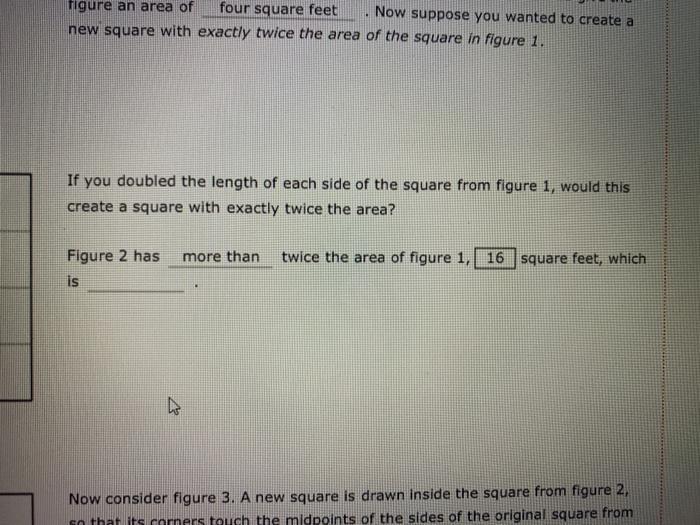
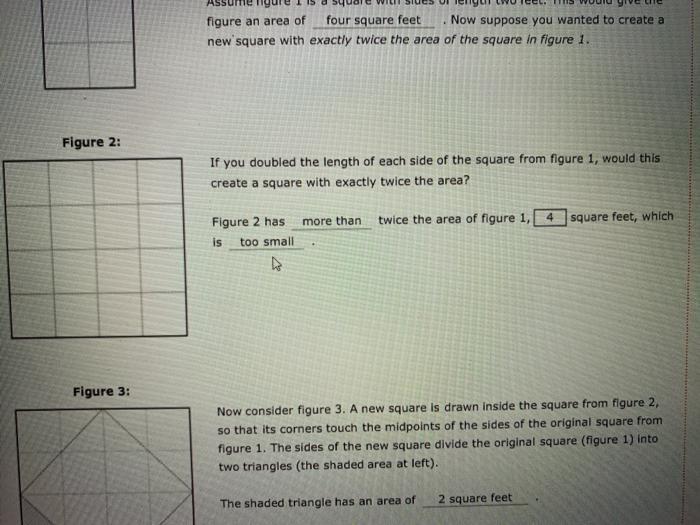
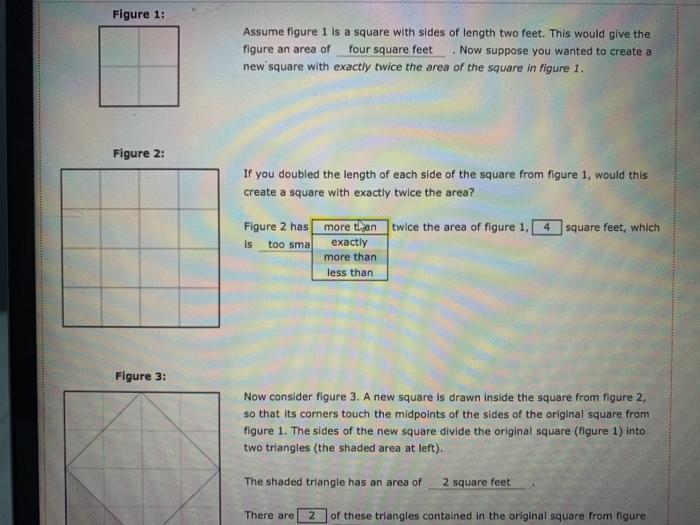
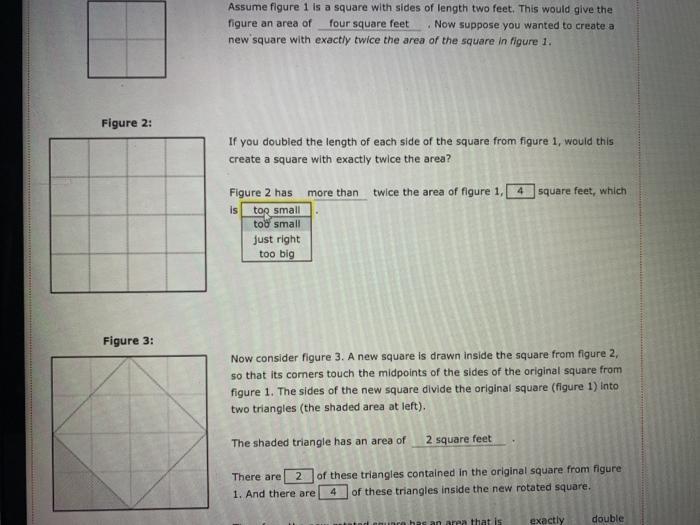
Figure 1: Figure 2: Figure 3: Assume figure 1 is a square with sides of length two feet. This would give the figure an area of four square feet . Now suppose you wanted to create a new square with exactly twice the area of the square in figure 1. If you doubled the length of each side of the square from figure 1, would this create a square with exactly twice the area? Figure 2 has is too sma more than twice the area of figure 1, 4 exactly more than less than square feet, which Now consider figure 3. A new square is drawn inside the square from figure 2, so that its corners touch the midpoints of the sides of the original square from figure 1. The sides of the new square divide the original square (figure 1) into two triangles (the shaded area at left). The shaded triangle has an area of 2 square feet There are 2 of these triangles contained in the original square from figure figure an area of four square feet Now suppose you wanted to create a new square with exactly twice the area of the square in figure 1. If you doubled the length of each side of the square from figure 1, would this create a square with exactly twice the area? Figure 2 has more than twice the area of figure 1, 16 square feet, which is Now consider figure 3. A new square is drawn inside the square from figure 2, so that its corners touch the midpoints of the sides of the original square from Figure 2: Figure 3: figure an area of four square feet Now suppose you wanted to create a new square with exactly twice the area of the square in figure 1. If you doubled the length of each side of the square from figure 1, would this create a square with exactly twice the area? Figure 2 has more than twice the area of figure 1, 4 is too small Now consider figure 3. A new square is drawn inside the square from figure 2, so that its corners touch the midpoints of the sides of the original square from figure 1. The sides of the new square divide the original square (figure 1) into two triangles (the shaded area at left). The shaded triangle has an area of square feet, which i 2 square feet Figure 1: Figure 2: Figure 3: Assume figure 1 is a square with sides of length two feet. This would give the figure an area of four square feet . Now suppose you wanted to create a new square with exactly twice the area of the square in figure 1. If you doubled the length of each side of the square from figure 1, would this create a square with exactly twice the area? Figure 2 has is too sma more than twice the area of figure 1, 4 exactly more than less than square feet, which Now consider figure 3. A new square is drawn inside the square from figure 2, so that its corners touch the midpoints of the sides of the original square from figure 1. The sides of the new square divide the original square (figure 1) into two triangles (the shaded area at left). The shaded triangle has an area of 2 square feet There are 2 of these triangles contained in the original square from figure Figure 2: Figure 3: Assume figure 1 is figure an area of new square with exactly twice the area of the square in figure 1. If you doubled the length of each side of the square from figure 1, would this create a square with exactly twice the area? twice the area of figure 1, 4 Figure 2 has is a square with sides of length two feet. This would give the four square feet Now suppose you wanted to create a too small too small just right too big more than Now consider figure 3. A new square is drawn inside the square from figure 2, so that its corners touch the midpoints of the sides of the original square from figure 1. The sides of the new square divide the original square (figure 1) into two triangles (the shaded area at left). There are 2 1. And there are The shaded triangle has an area of square feet, which 2 square feet of these triangles contained in the original square from figure 4 of these triangles inside the new rotated square. inre has an area that is exactly double