Fill out the table. please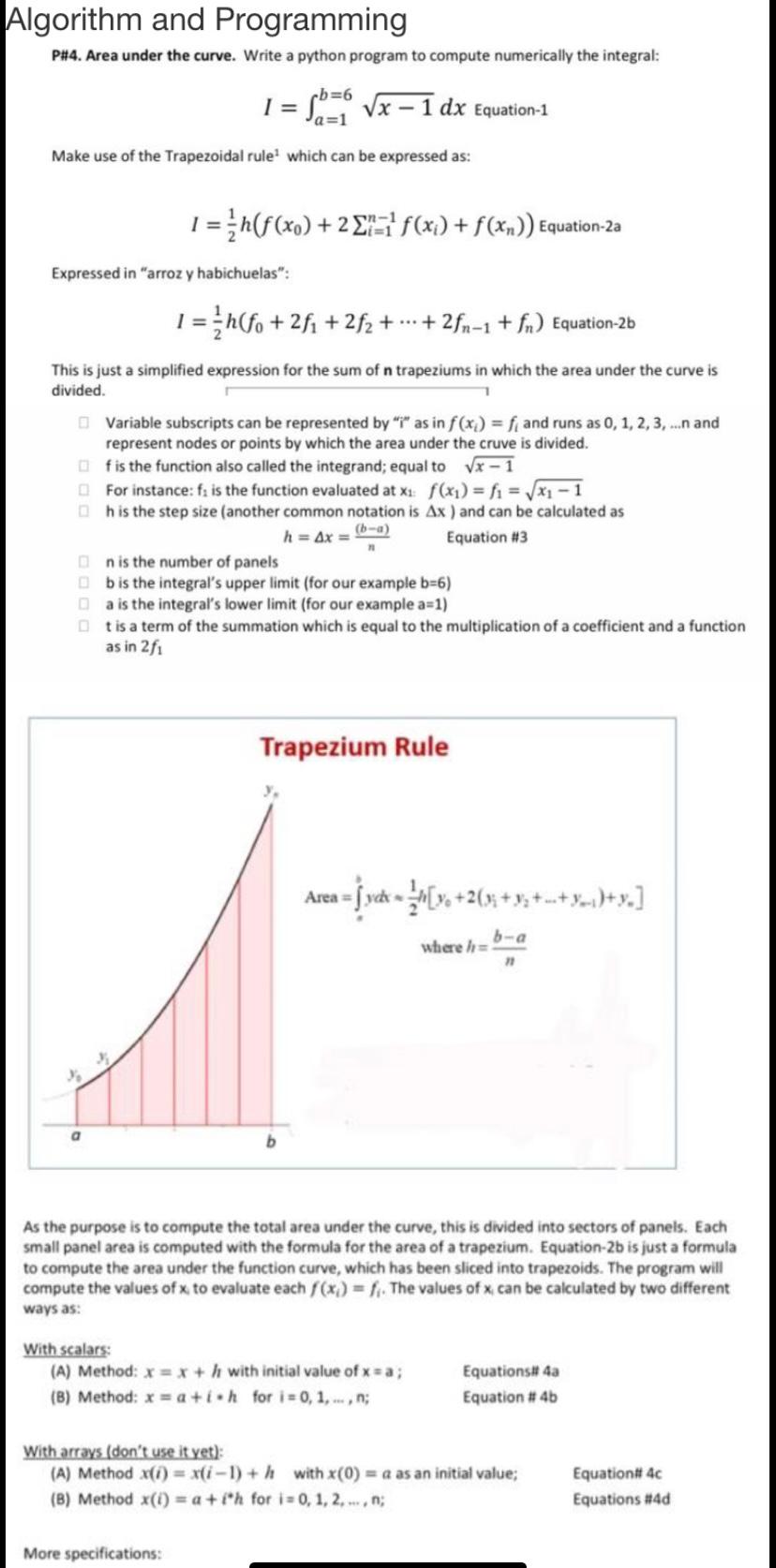

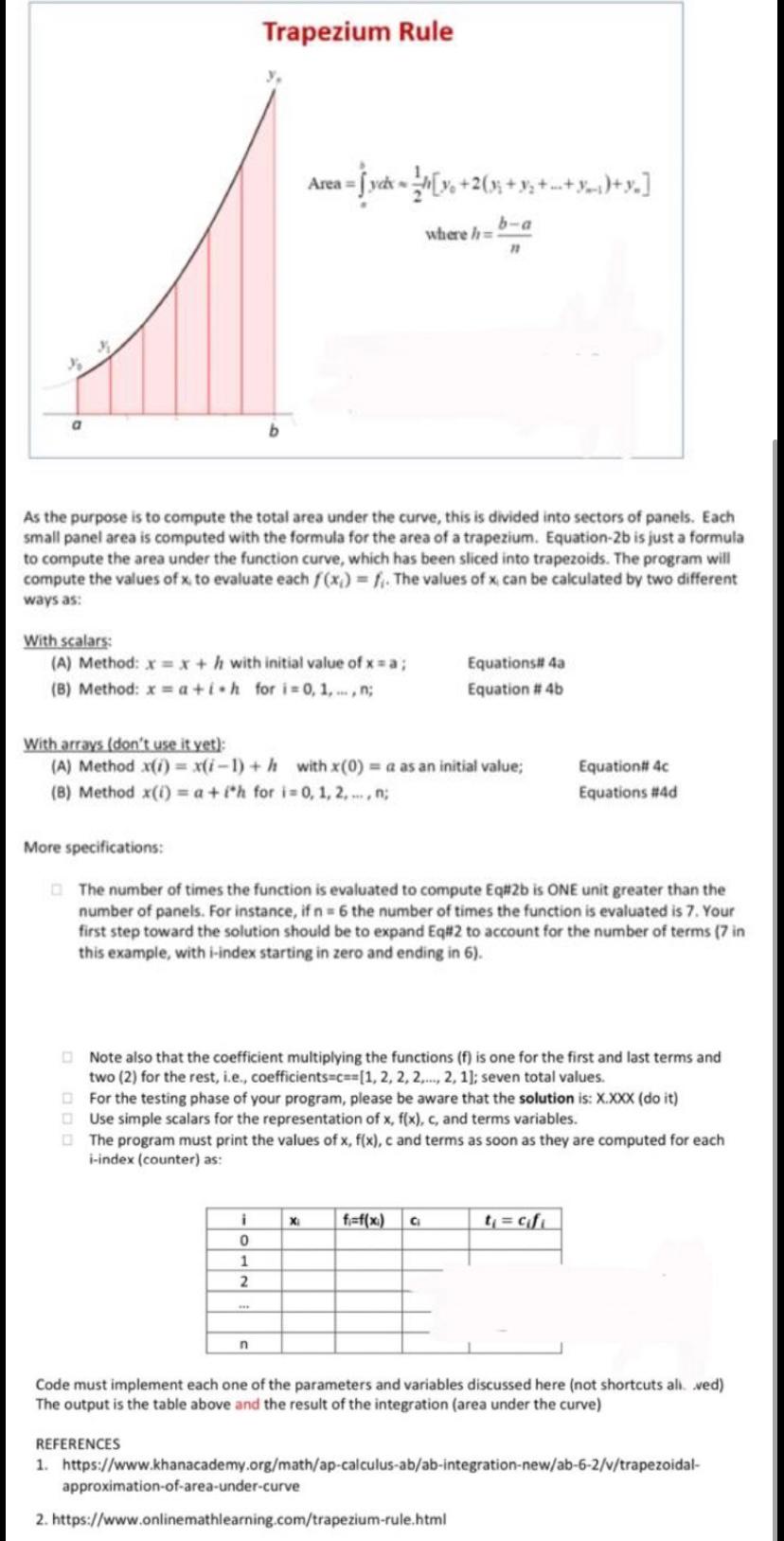
The picture is a bit unstructured. It is meant to be read continuosly. Ignore where stuff appears twice

Algorithm and Programming P#4. Area under the curve. Write a python program to compute numerically the integral: VX - 1 dx Equation-1 Ja=1 Make use of the Trapezoidal rule which can be expressed as: 1 == (f(xo) + 2 Er='f(x) + f(x-)) Equation-2a Expressed in "arroz y habichuelas": 1 = n(fo+2f1 +252 + ... +2fn-1 + fm) Equation-26 This is just a simplified expression for the sum of n trapeziums in which the area under the curve is divided. Variable subscripts can be represented by "#" as in f(x) = f and runs as 0, 1, 2, 3, ... and represent nodes or points by which the area under the cruve is divided. of is the function also called the integrand; equal to vx - 1 For instance: f; is the function evaluated at X1: f(x1) = f1 = 1X1 - 1 h is the step size (another common notation is Ax ) and can be calculated as h = ax = Equation #3 on is the number of panels Db is the integral's upper limit (for our example b=6) Da is the integral's lower limit (for our example a=1) It is a term of the summation which is equal to the multiplication of a coefficient and a function as in 2fi Trapezium Rule Area = jyck on [+2633+ y; +--+ --)+x.] where hb-a 71 a As the purpose is to compute the total area under the curve, this is divided into sectors of panels. Each small panel area is computed with the formula for the area of a trapezium. Equation-2b is just a formula to compute the area under the function curve, which has been sliced into trapezoids. The program will compute the values of x to evaluate each f(x) = f The values of x can be calculated by two different ways as: With scalars: (A) Method: x = x + h with initial value of x = a; (B) Method: x = a +ih for i=0,1,..., n; Equations# 4a Equation #46 With arrays (don't use it yet): (A) Method xi) = x(i-1) + h with x(0) = a as an initial value; (B) Method x(i) = a + l'h for i=0,1,2,.,; Equationit 40 Equations #40 More specifications: Trapezium Rule Area = vek [. +263 + y; ++ya) + x.] where h= a b As the purpose is to compute the total area under the curve, this is divided into sectors of panels. Each small panel area is computed with the formula for the area of a trapezium. Equation-2b is just a formula to compute the area under the function curve, which has been sliced into trapezoids. The program will compute the values of x to evaluate each f(x) = 1. The values of x can be calculated by two different ways as: With scalars: (A) Method: x= x + h with initial value of x = a; (B) Method: x = a +ion for i=0, 1,..., n; Equations# 4a Equation # 4b With arrays (don't use it yet): (A) Method x(i) = x(i-1) + h with x(0) = a as an initial value; (B) Method X(t) = a + *h for i=0, 1, 2, ...; Equation 4c Equations #40 More specifications: The number of times the function is evaluated to compute Eq#2b is ONE unit greater than the number of panels. For instance, if n = 6 the number of times the function is evaluated is 7. Your first step toward the solution should be to expand Eq#2 to account for the number of terms (7 in this example, with i-index starting in zero and ending in 6). Note also that the coefficient multiplying the functions (f) is one for the first and last terms and two (2) for the rest, i.e., coefficients=c==[1, 2, 2, 2,..., 2, 1); seven total values. For the testing phase of your program, please be aware that the solution is: X.XXX (do it) Use simple scalars for the representation of x, f(x), c, and terms variables. The program must print the values of x, f(x), c and terms as soon as they are computed for each i-index (counter) as: f=f(x) C t=cf i 0 1 2 n Code must implement each one of the parameters and variables discussed here (not shortcuts al ved) The output is the table above and the result of the integration (area under the curve) REFERENCES 1. https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-2/v/trapezoidal- approximation-of-area-under-curve 2. https://www.onlinemathlearning.com/trapezium-rule.html