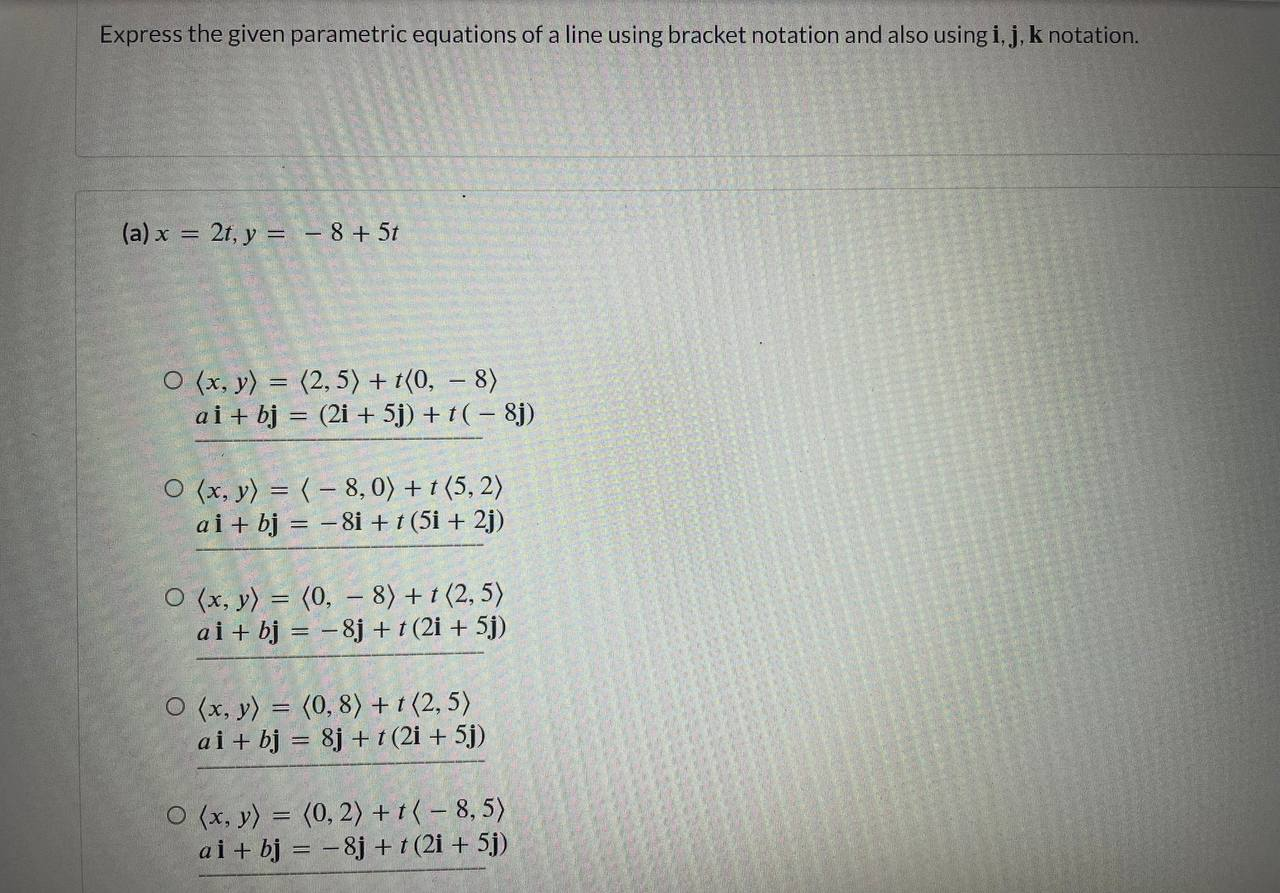
Find parametric equations of the line through (-3, 1, 6) that is parallel to 4i-8j+k. x(t) = y(t) = z(t) = Find the distance between the skew lines: x = 5+7t, y=3+7t, z = 8-9t x = 1-t, y = 6, z = 5+8t NOTE: Enter the exact answer. D = Express the given parametric equations of a line using bracket notation and also using i, j, k notation. (a) x = 2t, y = -8 +5t O (x, y) = (2,5) + t(0, - 8) ai+bj = (21+ 5j) + t ( - 8j) O(x, y) = (-8,0) + t (5, 2) ai + bj = -8i + t (5i + 2j) O (x, y) = (0, -8) + t (2,5) ai+ bj = -8j+t (2i + 5j) O(x, y) = (0,8) + t (2,5) ai+ bj = 8j+t (2i+ 5j) O (x, y) = (0, 2) + t( - 8,5) ai + bj = -8j+ t (2i + 5j) (b) x = 6+ 6t,y = 4+10t, z = 7-4t O (x, y, z) = (6, ai+bj+ck = 4, 7) + t (6, 10, 4) == (61-4j +7k) + t (61 + 10j - 4k) O (x, y, z) = (6, 4, 7) + t (6, 10, 4) ai + bj + ck = (6i + 4j +7k) + t (6i + 10j + 4k) O (x, y, z) = (-6, 10, 4) + ( 6, 4, 7) ai+bjck = ( - 6i - 10j + 4k) + (-6i + 4j - 7k) O (x, y, z) = (6, 10, 4) + t (6, - 4,7) ai + bj + ck = (6i + 10j - 4k) + (6i - 4j + 7k) O (x, y, z) = (-6, 4, 7) +t(-6, - 10,4) ai+bjck = (-6i + 4j7k) + ( 6i - 10j + 4k) Find parametric equations of the line that satisfies the stated conditions. The line through (-4, 0, 3) that is parallel to the line x = 1 + 7t, y = 2 t, z = 8+ 3t. Ox=7-4t, y = -1, z= 3 + 3t O x = -4+7t, y = 1, z = 3 + 3t O x = -4+7t, y = -t, z = 3 + 3t O x = 7 - 4t, y = 1, z = 3 + 3t Ox=-4-7t, y = t, z = 3 - 3t