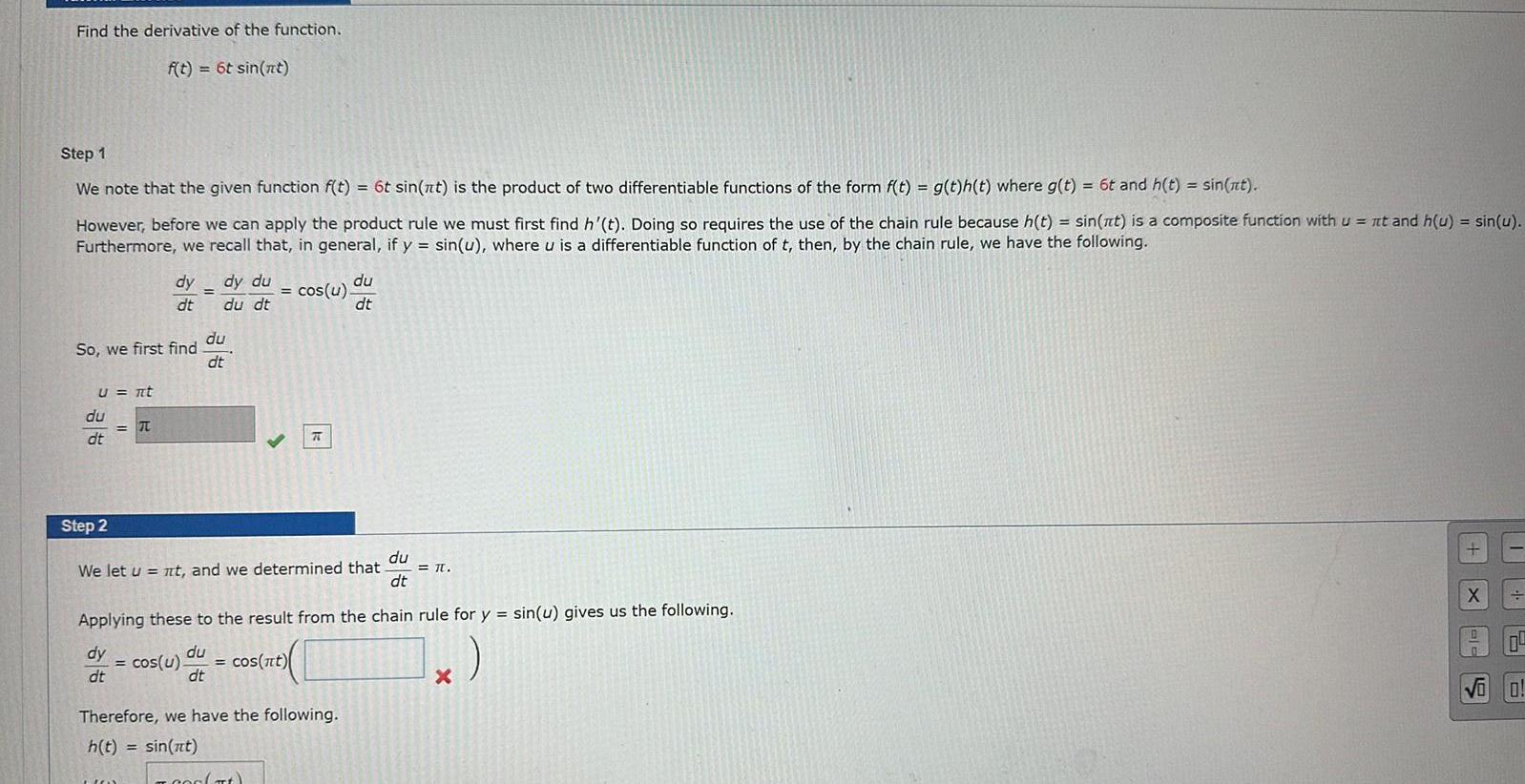
Find the derivative of the function. f(t)=6t sin(at) Step 1 We note that the given function f(t) = 6t sin(t) is the product of two differentiable functions of the form f(t) = g(t)h(t) where g(t) = 6t and h(t) = sin(t). However, before we can apply the product rule we must first find h'(t). Doing so requires the use of the chain rule because h(t) = sin(t) is a composite function with u = t and h(u) = sin(u). Furthermore, we recall that, in general, if y = sin(u), where u is a differentiable function of t, then, by the chain rule, we have the following. dy dy du du = dt du dt = cos(u). dt So, we first find du dt U = It du = dt Step 2 du We let ut, and we determined that = 10. dt Applying these to the result from the chain rule for y = sin(u) gives us the following. dy du = cos(u)- == cos(at) dt dt Therefore, we have the following. h(t)=sin(at) x X 0 Vi 0!