Find the Laplace transforms of tcos(at) and t^2cos(at). Do this without using the integral definition of the Laplace transform by starting with the transform of cos(at).

So this is what I did:

The transform of cos(at) is:

So taking the negative derivative of that with respect to s will give the Laplace transform for tcos(at), correct?

I got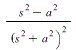

Then taking the negative derivative of that shoul then give the transform for t^2cos(at).

Doing that I got: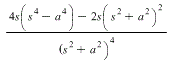

Can anyone verify these answers or tell me where I went wrong? Thanks

Transcribed Image Text:

S + a S + a

Answer rating: 100% (QA)

We have of We have formula d Fs Laplace transform of ds Here Fs is Laplace transform of function flt ... View the full answer