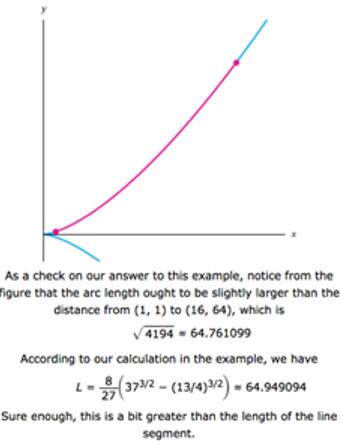
Find the length of the arc of the semicubical parabola y2 = x between the points (1, 1) and (16, 64). (See the figure.) SOLUTION For the top half of the curve we have y=x/2 dy 3 and so the arc length formula gives V1+ 64 16 x dx. If we substitute u- then du - dx. When x = 1, L = 16 16 - [0 + (OX) x = [ dx ; when x = 16, u= Vu du 137 13/4 Therefore, As a check on our answer to this example, notice from the figure that the arc length ought to be slightly larger than the distance from (1, 1) to (16, 64), which is 4194-64.761099 According to our calculation in the example, we have (373/2 (13/4)3/2) - 64.949094 Sure enough, this is a bit greater than the length of the line segment.