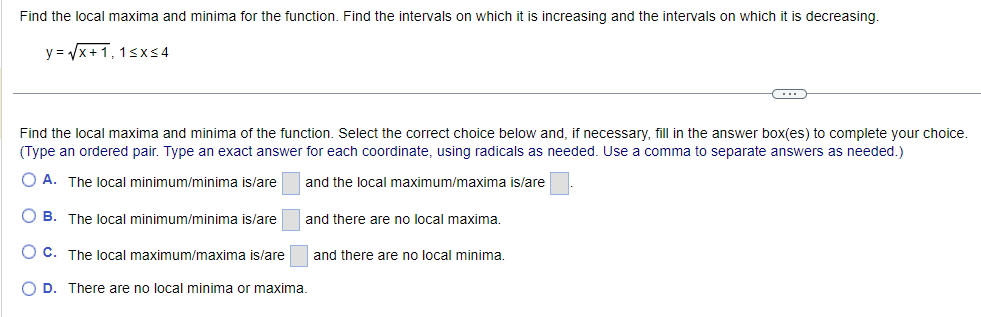
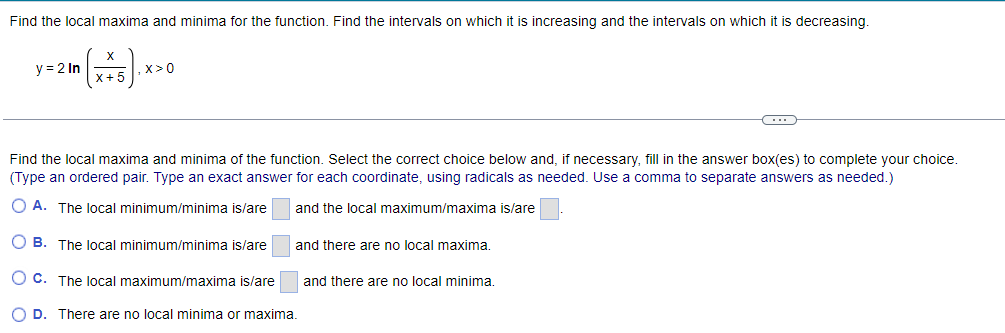
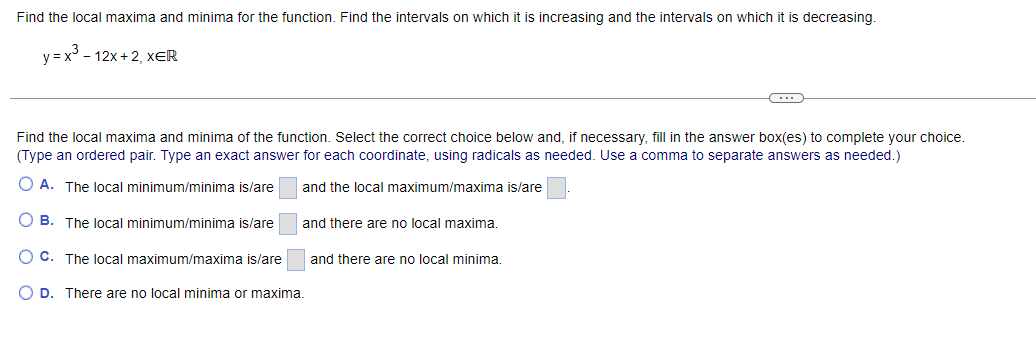
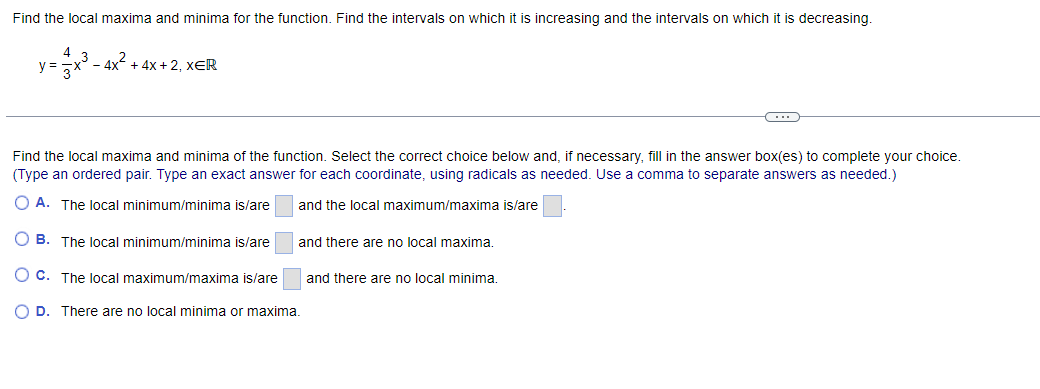
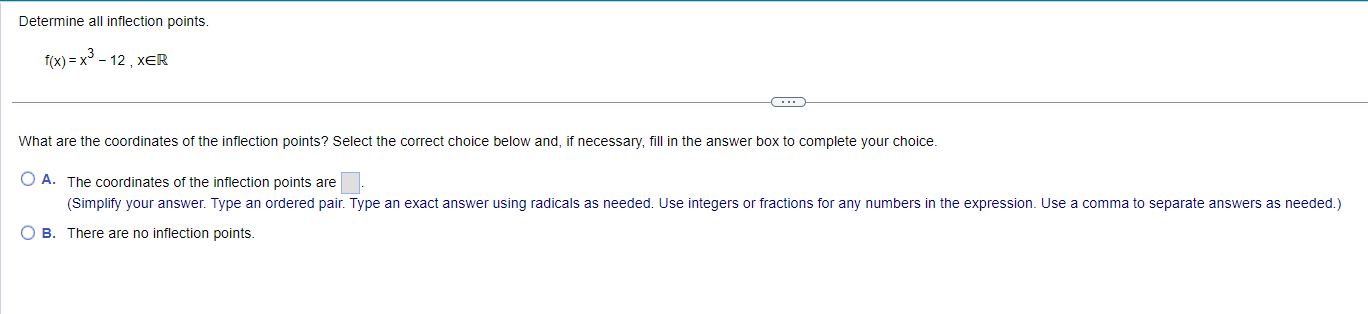
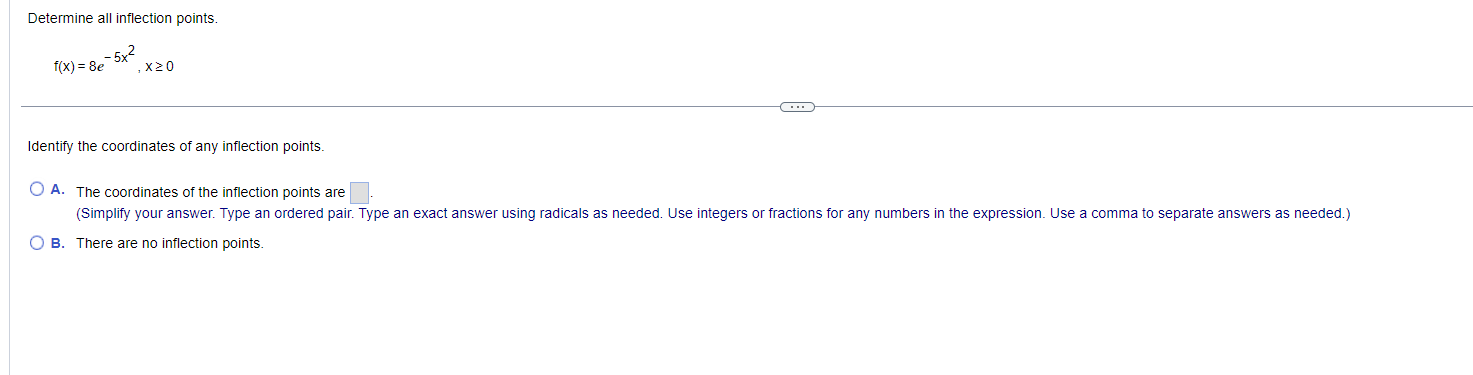
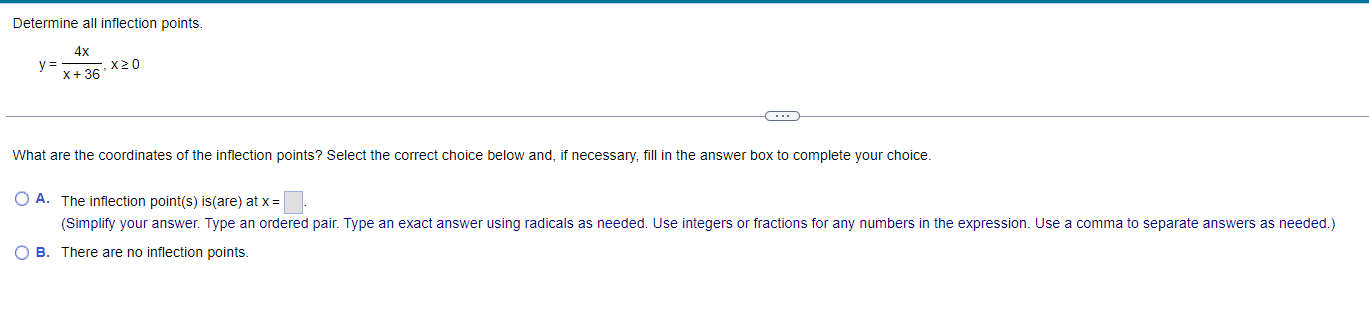
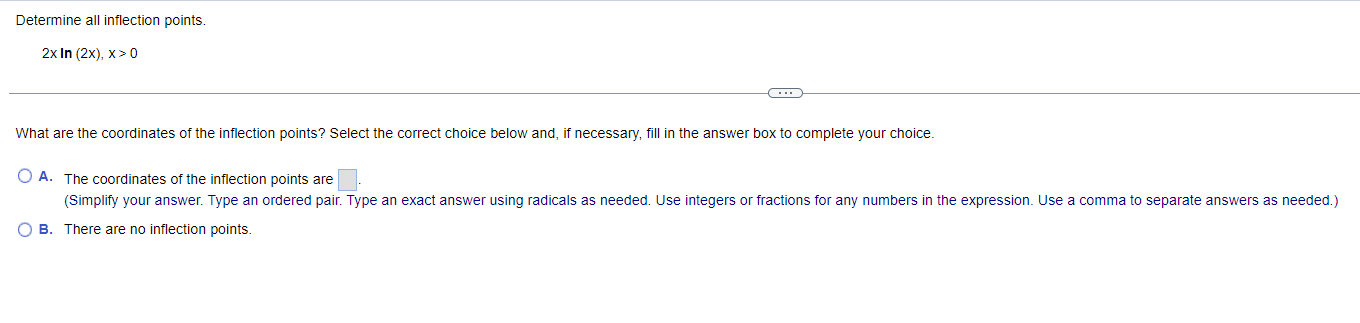
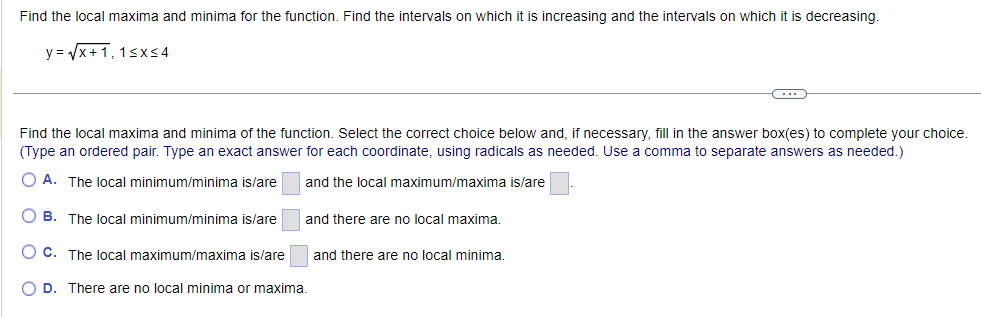
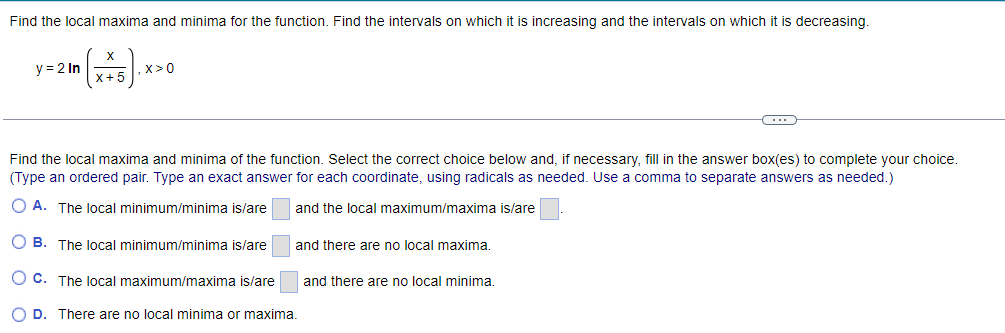
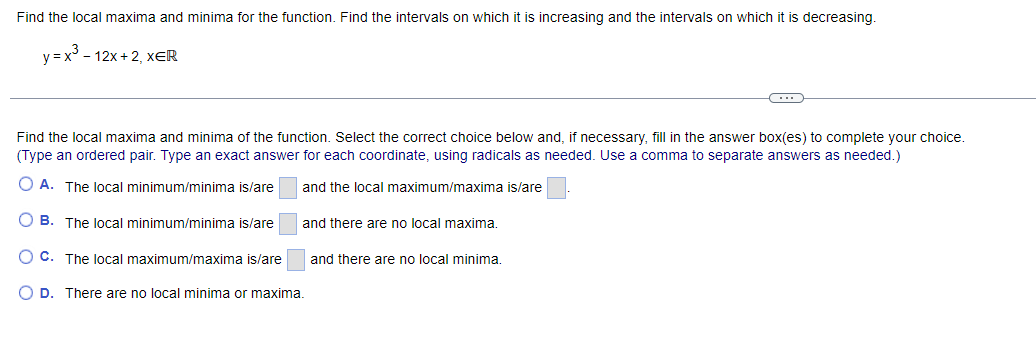
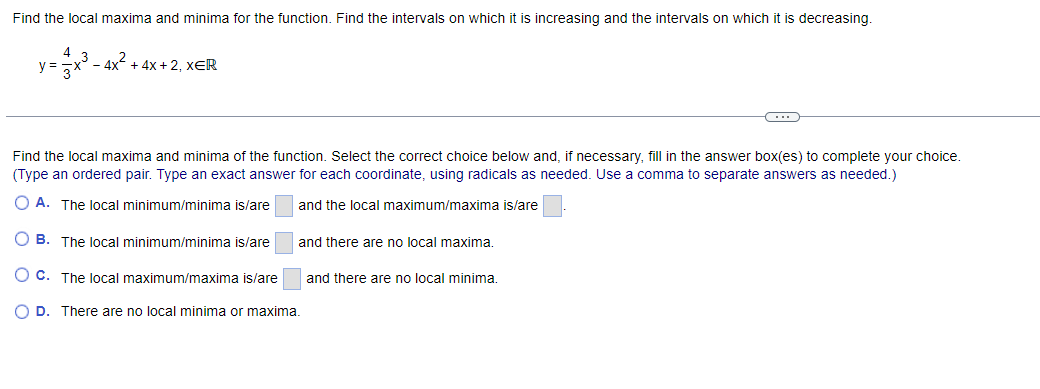
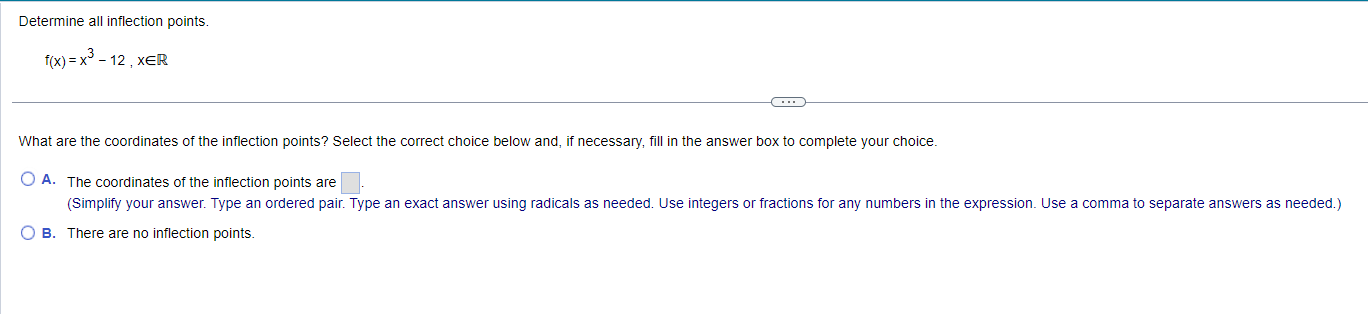
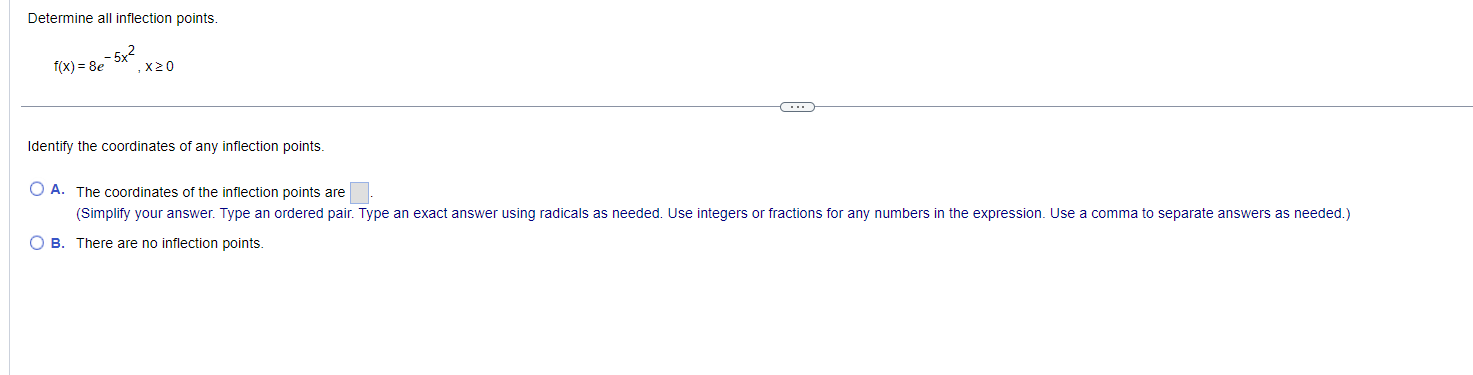
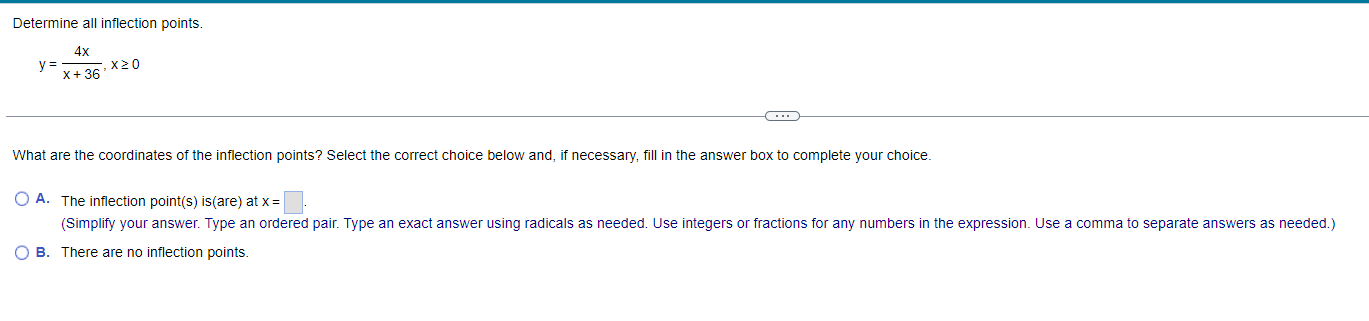
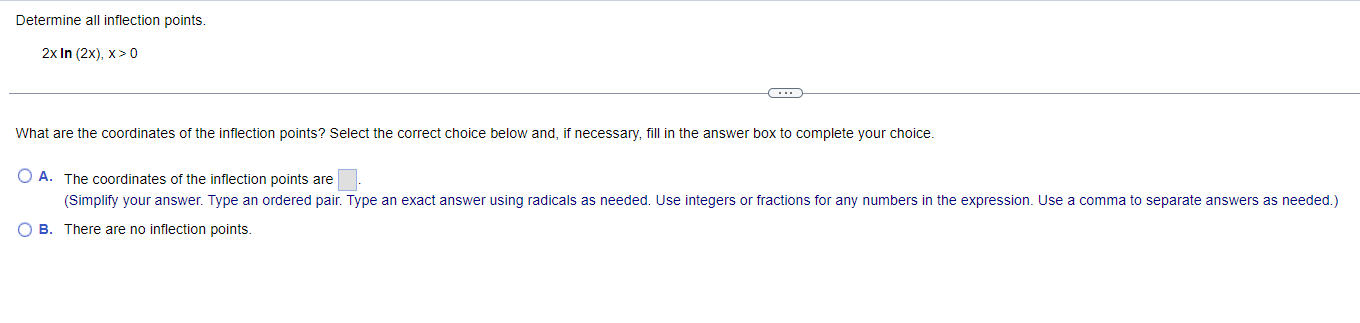
Find the local maxima and minima for the function. Find the intervals on which it is increasing and the intervals on which it is decreasing. y= vX + 1, 1sx54 . . . Find the local maxima and minima of the function. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. (Type an ordered pair. Type an exact answer for each coordinate, using radicals as needed. Use a comma to separate answers as needed.) O A. The local minimum/minima is/are and the local maximum/maxima is/are O B. The local minimum/minima is/are and there are no local maxima. O C. The local maximum/maxima is/are and there are no local minima. O D. There are no local minima or maxima.Find the local maxima and minima for the function. Find the intervals on which it is increasing and the intervals on which it is decreasing. X y = 2 In X+5 1X20 Find the local maxima and minima of the function. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. (Type an ordered pair. Type an exact answer for each coordinate, using radicals as needed. Use a comma to separate answers as needed.) O A. The local minimum/minima is/are and the local maximum/maxima is/are O B. The local minimum/minima is/are and there are no local maxima. O C. The local maximum/maxima is/are and there are no local minima. O D. There are no local minima or maxima.Find the local maxima and minima for the function. Find the intervals on which it is increasing and the intervals on which it is decreasing. y= x - 12x + 2, XER . . . Find the local maxima and minima of the function. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. (Type an ordered pair. Type an exact answer for each coordinate, using radicals as needed. Use a comma to separate answers as needed.) O A. The local minimum/minima is/are and the local maximum/maxima is/are O B. The local minimum/minima is/are and there are no local maxima. O C. The local maximum/maxima is/are and there are no local minima. O D. There are no local minima or maxima.Find the local maxima and minima for the function. Find the intervals on which it is increasing and the intervals on which it is decreasing. 4 3 y = 2 x - 4x + 4x + 2, XER . . . Find the local maxima and minima of the function. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. (Type an ordered pair. Type an exact answer for each coordinate, using radicals as needed. Use a comma to separate answers as needed.) O A. The local minimum/minima is/are and the local maximum/maxima is/are O B. The local minimum/minima is/are and there are no local maxima. O C. The local maximum/maxima is/are and there are no local minima. O D. There are no local minima or maxima.Determine all inflection points. f(x) = x3 - 12 , XER What are the coordinates of the inflection points? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The coordinates of the inflection points are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) O B. There are no inflection points.Determine all inflection points. f(x) = Be - 5x2 , X20 Identify the coordinates of any inflection points. O A. The coordinates of the inflection points are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) O B. There are no inflection points.Determine all inflection points. 4x y= - X + 36' , X20 What are the coordinates of the inflection points? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The inflection point(s) is(are) at x = (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) O B. There are no inflection points.Determine all inflection points. 2x In (2x), X > 0 What are the coordinates of the inflection points? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The coordinates of the inflection points are (Simplify your answer. Type an ordered pair. Type an exact answer using radicals as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) O B. There are no inflection points.Hill's equation for the oxygen saturation of blood states that the level of oxygen saturation (fraction of hemoglobin molecules that are bound to oxygen) in blood can be represented by the following function, where P is the oxygen concentration around the blood (P 2 0) and n is a parameter that varies between different species. Answer parts (a) through (f) below. pn f(P) = p + 307 (a) Assume the n = 1. Show that f(P) is an increasing function of P and that f(P)-1 as P-co. Choose the correct answer below. O A. P 60 D If n = 1, f( P ) = P + 30 - and f'(P) = - The function f(P) is an increasing function since the slope of the curve y = f(P) is always negative. As P-co, lim f(P) = lim P + 30 -= lim - =1 (P + 30) P-+co P-+co P-00 O B. P 60 P If n = 1, f(P) = 1 P + 30 and f' (P) = The function f(P) is an increasing function since the slope of the curve y = f(P) is always positive. As P-+co, lim f(P) = lim lim - = 1. (P + 30) P-+co P-+co P + 30 P-+0o O c. P 30 P If n = 1, f(P ) = P + 30 - and f'(P) = The function f(P) is an increasing function since the slope of the curve y = f(P) is always positive. As P-co, lim f(P) = lim = lim (P + 30)2 P-+co P-+00 P + 30 P-+ 00 O D. P 30 P If n = 1, f(P) = P + 30 and f'(P) = - ". The function f(P) is an increasing function since the slope of the curve y = f(P) is always negative. As P-co, lim f(P) = lim (P +30)- P + 30 lim 1 P-+0o P-+0o P-00