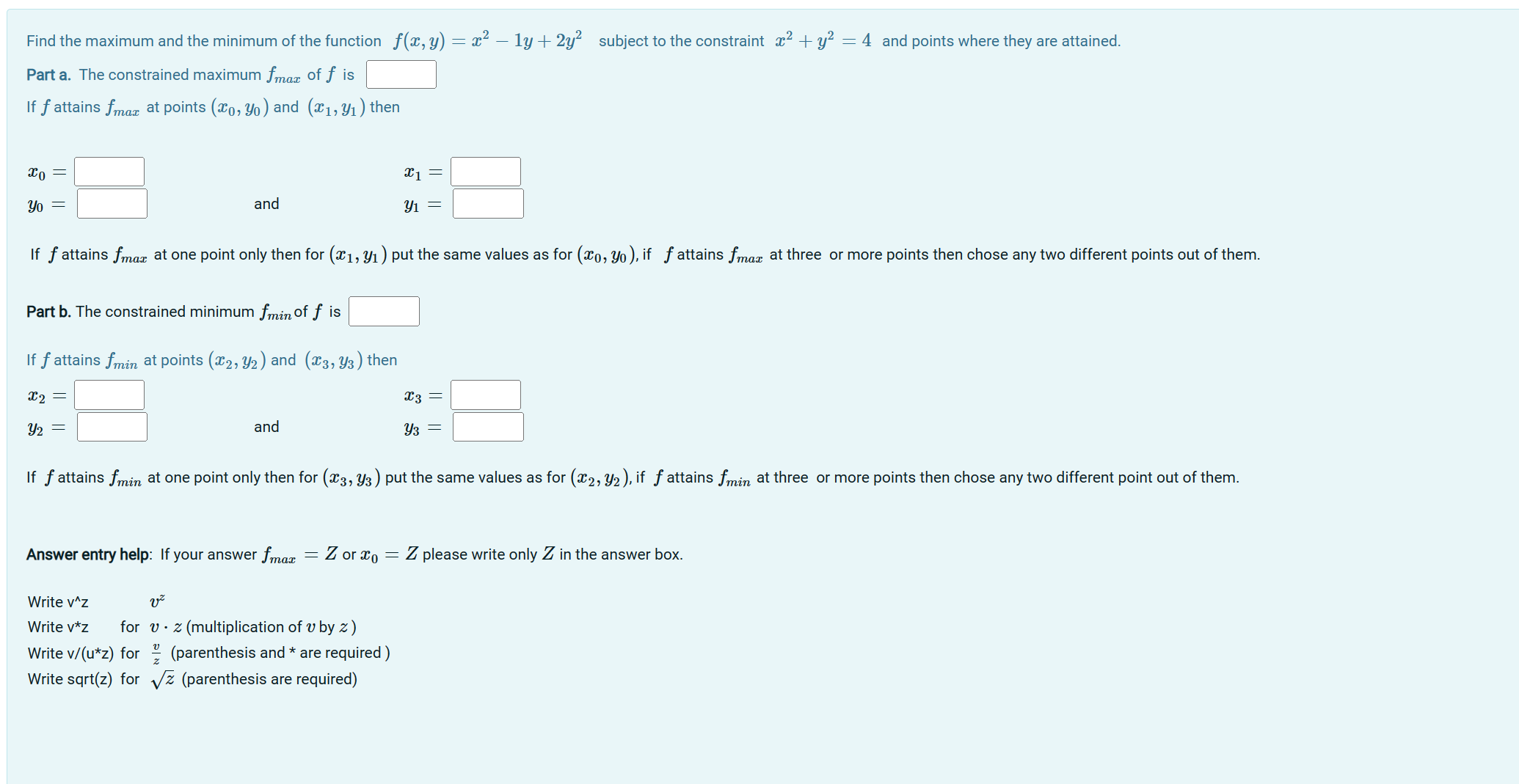
Find the maximum and the minimum of the function f(x, y) = x - ly+2y subject to the constraint x + y = 4 and points where they are attained. Part a. The constrained maximum fmax of is If f attains fmax at points (x0, yo) and (x1,y1 ) then x0 = and x1 = . Y1 If f attains fmax at one point only then for (x1,y1) put the same values as for (x0, yo), if attains fmax at three or more points then chose any two different points out of them. Part b. The constrained minimum fmin of is If f attains fmin at points (x2, y2) and (x3, Y3) then x2 = Y2 and x3 = Y3 If attains min at one point only then for (x3, Y3) put the same values as for (x2, y2), if attains fmin at three or more points then chose any two different point out of them. Answer entry help: If your answer fmax = Z or x = Z please write only Z in the answer box. Write v^z Write v*z for v(multiplication of by z) Write v/(u*z) for 2 (parenthesis and * are required) Write sqrt(z) for 2 (parenthesis are required)