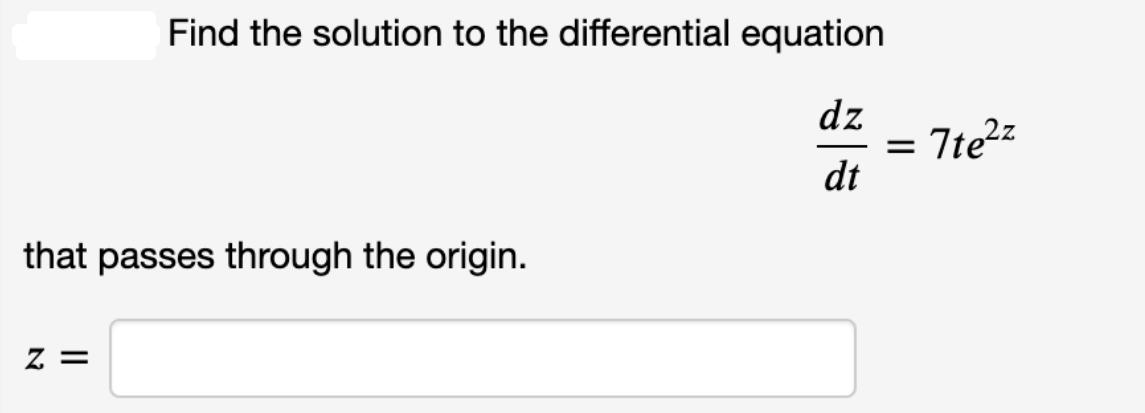
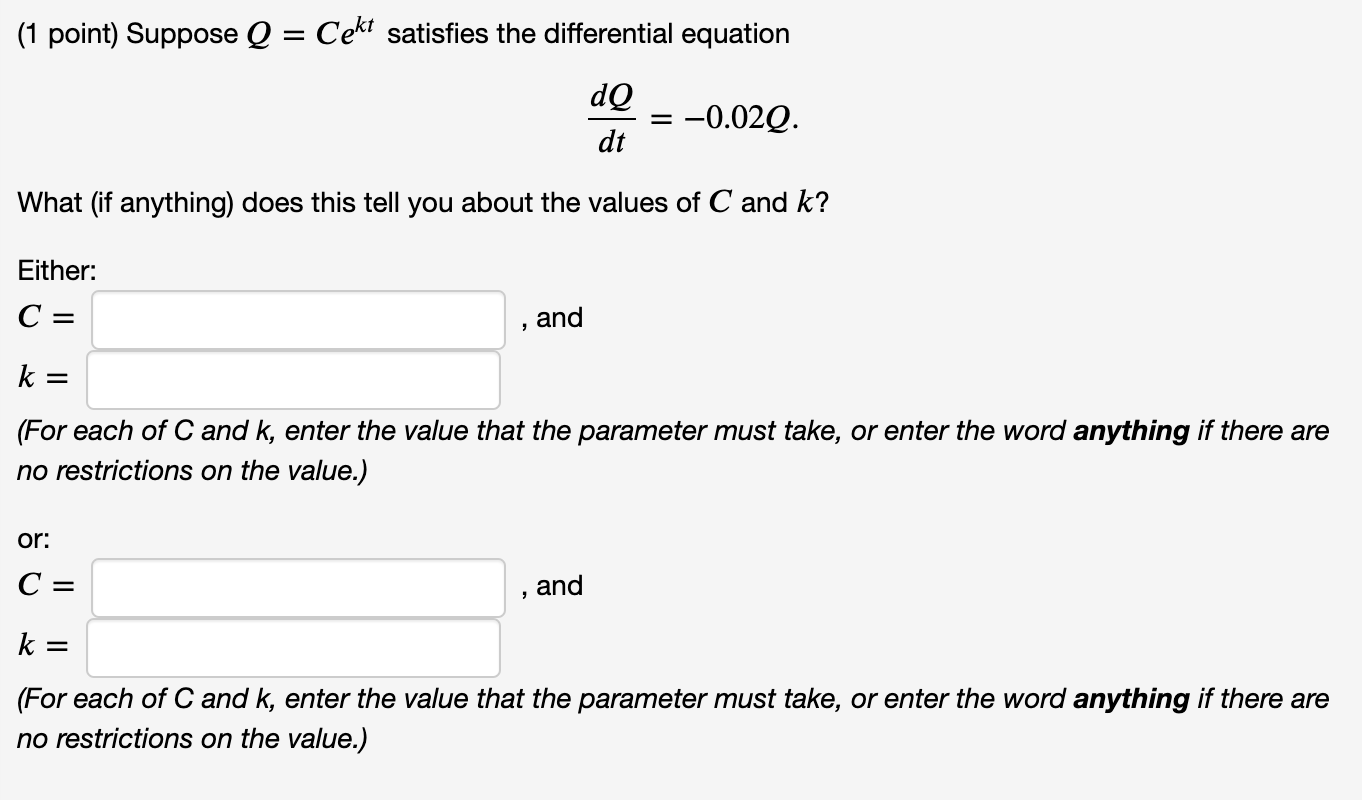
Find the solution to the differential equation dz dt that passes through the origin. Z = = 7tez (1 point) Verify that every member of the family of functions y = equation xy + xy = 1. Answer the following questions. In x + C X is a solution of the differential 1. Find a solution of the differential equation that satisfies the initial condition y(3) = 2. Answer: y = 2. Find a solution of the differential equation that satisfies the initial condition y(2) = 3. Answer: y = (1 point) Find k such that x(t) = 13 is a solution of the differential equation k = dx dt = : kx. (1 point) Suppose Q = Cekt satisfies the differential equation dQ dt What (if anything) does this tell you about the values of C and k? Either: C = k = (For each of C and k, enter the value that the parameter must take, or enter the word anything if there are no restrictions on the value.) or: C = and and = -0.02Q. k = (For each of C and k, enter the value that the parameter must take, or enter the word anything if there are no restrictions on the value.)