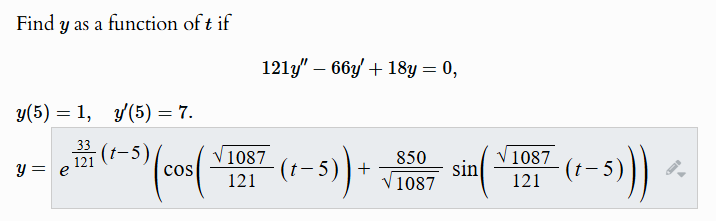
Find y as a function of t if 121y" - 66y' + 18y = 0, y(5) = 1, y'(5) = 7. 33 y = e 121 (t-5) 1087 850 1087 cos (+ - 5 ) 121 (+- 5 ) + sin V 1087 121FGT'I Help me with this Let's solve a similar problem step-by-step to understand the concepts better. Find g as a funcrion of if 16y" 64y + 89y = 0, Here's a step-by-step solution guide. Step 1 It is helpful to notice that if u(t) = y( + 1), then u satishes the same differential equation as y, and the initial conditions are u(0) = 2 and w'(0) = 2. Can you use the auxiliary equation to find the general solution for uw? Step 2 The auxiliary equation is 167? 64r + 89 = 0, which has the roots r = 2 + %i. The general solution for u 15 w et (cl cos (%t) + o8in (%t}] Can you use the initial conditions to find ; and y? Step 3 The derivative of the solution is u = 2e% (e1cos (%t} + cp8in (%t)) + e (%cl sin {%t) + 2cocos (%t)) The initial conditions lead to the equarions = Cl = 2+ 3 1 4\"2 and the solution is (c1, 2) = (2, o %) The solution of the initial value problem for u is u(t) = e (2 cos (%t} 2 sin (%t)), and the solution for y() = u(t 1) is y(t) = e** V) (2cos (2(t 1)) Esin (3(1))). I need help solving my problem at the top. | posted a similar question to help solve my problem. | am confused and need further explanation than the help tab is providing me. Problem 7. (1 polat) Find y as a function of f if 91"- 367 + 52y =0, )(5) = 2, y'(5) =5. * = Solution: SOLUTION First note that the initial conditions are given at / - 5. To simplify the computations, we introduced the new function u(r) = y(r +5). The function a satisfies the differential equation 9w" -36u' + 52# =0, and its initial conditions are "(0) = >(5) - 2, #'(0) =>(5) =5 We will solve the initial value problem for the function # and then evaluate the function y(r) = (1 -5). The characteristic equation is 9/2- 36r +52 =0. Using the quadratic formula we find the roots riz = 2 + / and the general solution can be written as u =e" (ci cos (jr) + ezsin ($1)), for which if' = 22" (ci cos (jr) +casin (go)) te" ( jessin (;) + 162 cos Substituting the initial conditions gives the system CI with solution cl = 2, c2 - 1. Hence the function & is given by "(1) = (2cos (;1) + } sin (1:)) Thus the solution to the initial value problem is y(1) = 20-5) (2cos (1(1 -5)) + 1 sin (3(1 -5))) Correct Answers: (2) * (exp [ (2) . (t - 5 )1) * (cos( (4/3) . (t - 5 )1) + (3/4) .le