FIRST I WILL PROVIDE MY QUESTION WITH ITS DATA, THEN I WILL PROVIDE AN EXAMPLE OF HOW ITS SUPPOSE TO BE DONE UNDERNEATH TO ASSIST YOU

My question:

Euro/Japanese Yen.

A French firm is expecting to receive 10.4 million in 90 days as a result of an export sale to a Japanese semiconductor firm. What will it cost, in total, to purchase an option to sell the yen at 0.0072/? (See table for initial values.)

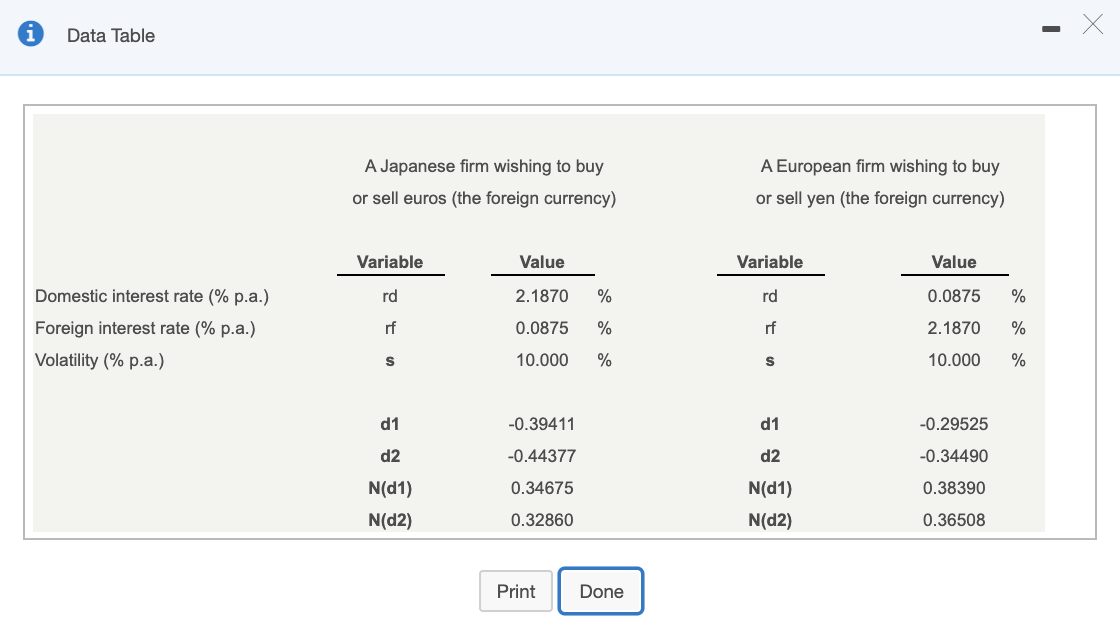The cost, in total, to purchase an option to sell the yen at 0.0072/JPY is ____________/. (Round to the nearest cent.) --> please make answer clear

An Example:

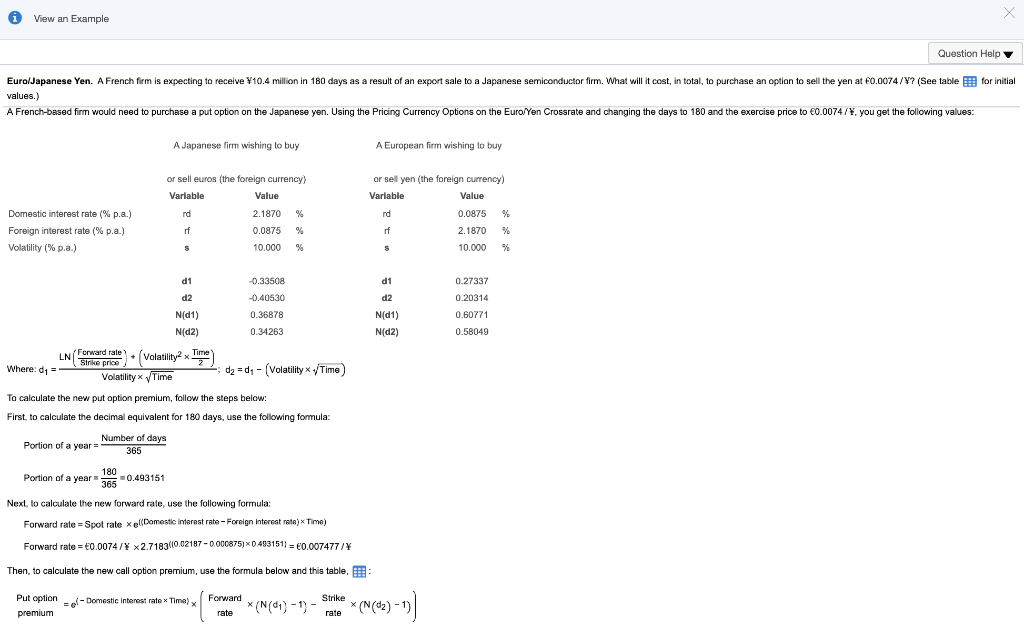
Data Table - A Japanese firm wishing to buy or sell euros (the foreign currency) A European firm wishing to buy or sell yen (the foreign currency) Variable Value Variable Value rd 2.1870 % rd 0.0875 % Domestic interest rate (% p.a.) Foreign interest rate (% p.a.) Volatility (% p.a.) rf 0.0875 % rf 2.1870 % 10.000 % S 10.000 % s d1 d1 -0.29525 -0.39411 -0.44377 d2 d2 -0.34490 0.34675 0.38390 N(D1) N(D2) N(D1) N(D2) 0.32860 0.36508 Print Done View an Example Question Help Euro/Japanese Yen. A French firm is expecting to receive 10.4 million in 180 days as a result of an export sale to a Japanese semiconductor firm. What will it cost, in total, to purchase an option to sell the yen at 0.0074/? (See table for initial values.) A French-based firm would need to purchase a put option on the Japanese yen. Using the Pricing Currency Options on the Euro/Yen Crossrate and changing the days to 180 and the exercise price to 0.0074/, you get the following values: A Japanese firm wishing to buy A European firm wishing to buy or sell euros (the foreign currency) Variable Value or sell yen (the foreign currency) Variable Value nd 2.1870 % nd % Domestic interest rate (% p.a.) Foreign interest rate (% p.a.) Volatility (% p.a.) rf 0.0875 % rf 0.0875 2.1870 10.000 % 10.000 % s % d1 0.27337 d2 -0.33508 -0.40530 0.36878 d1 d2 N(D1) Nd2) ) 0.20314 0.60771 N(1) Nd2) 0.34263 0.58049 Time Where: da LN('crward rale) + (Volatility2 x " Strike Volatility Time dz = d.- (Volatility /Time) To calculate the new put option premium, follow the steps below: First, to calculate the decimal equivalent for 180 days, use the following formula: Portion of a year Number of days 365 180 Portion of a year 385 +0.493151 Next, to calculate the new forward rate, use the following formula: Forward rate=Spot rate xel(Domestic Interest rate - Foreign Interest rate) Time) Forward rate = 0.0074/ x 2.7183(10.02187 -0.000875) *0.493151) = 0.007477/ Then, to calculate the new call option premium, use the formula below and this table, Put option -- Domestic interest rate x Time) premium Forward x((1 * (N(41) - 1) rate sprake Put option premium Total cost =10,400,000 ~ 0.000150 /\ = 1,560.00