First of all I really apologize for sending you question like this but I had to PhotoGrid them to make it in all ones but these are the question I really need help with, please help me on this question to answer it correctly, you can totally zoom in and be able to see questions and you will understand question flow that which question is goes with other one and mainly please also answer the graphs too below please I really understand and apologize for being this tiny questions and not able to put in correct way but you will get it and zoom in to see it please I really do beg you to solve it all of them correctly please and I really appreciate and hardwork also for your time thanks a lot! :)
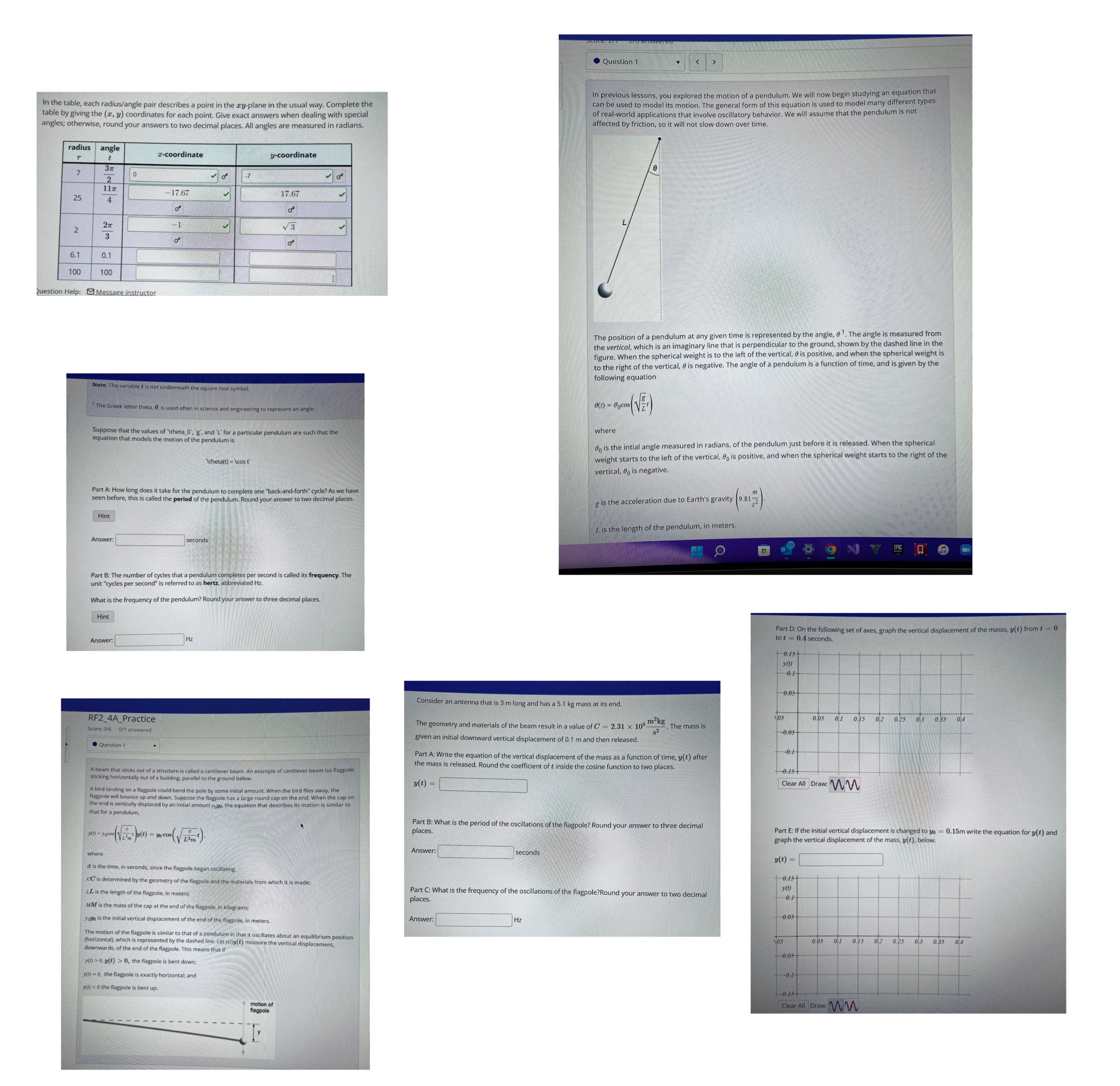
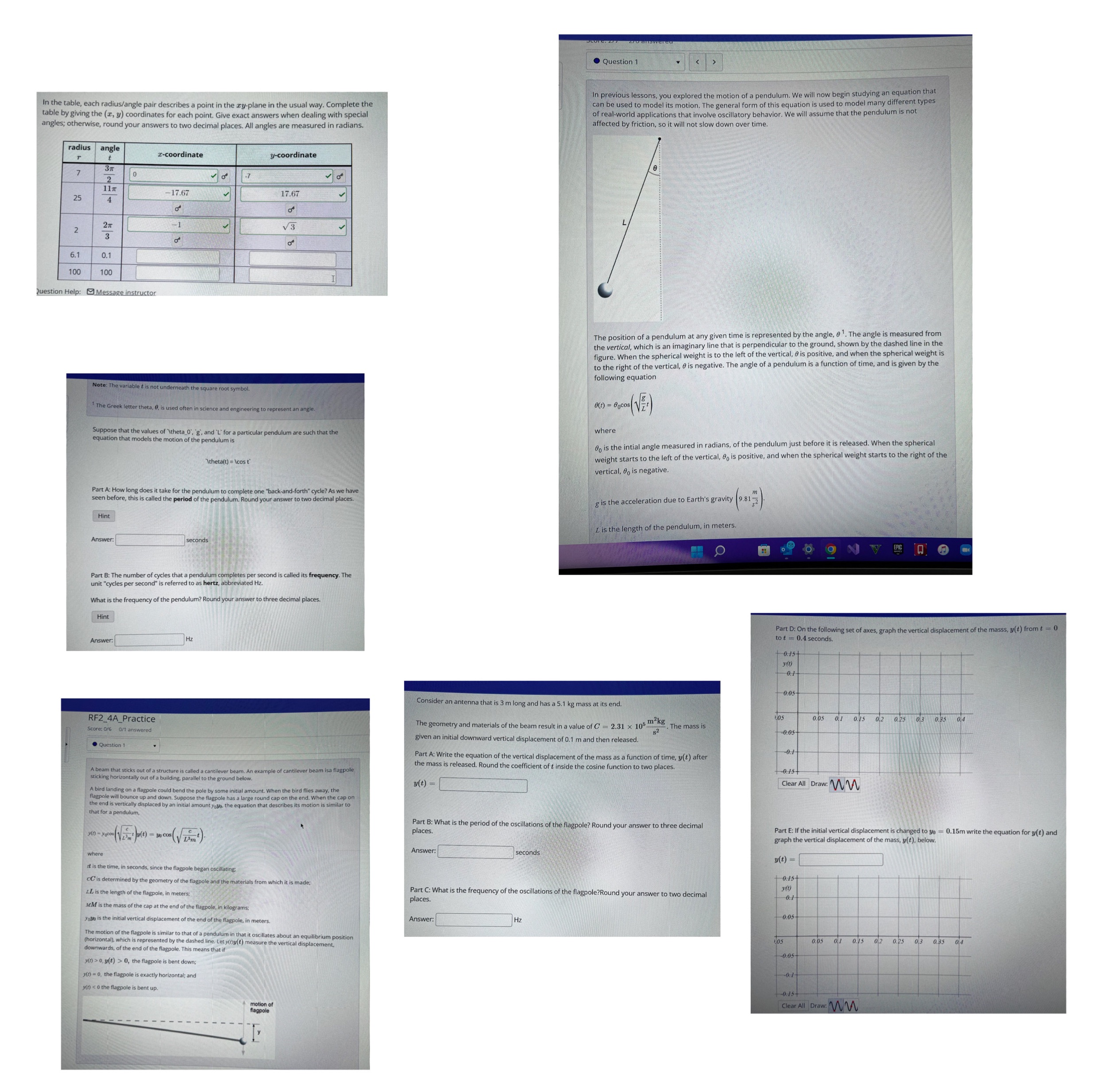
. Question 1 In previous lessons, you explored the motion of a pendulum. We will now begin studying a egin studying an equation that In the table, each radius/ angle pair describes a point in the cy-plane in the usual way. Complete the can be used to model its motion. The general form of this equation is used to model many different types table by giving the (z, y) coordinates for each point. Give exact answers when dealing with special of real-world applications that involve oscillatory behavior. We will assume that the pendulum is not angles; otherwise, round your answers to two decimal places. All angles are measured in radians. ed by friction, so it will not slow down over time. radius angle I-coordinate y-coordinate 2 10 -7 25 17.67 17.67 3 V3 6.1 0.1 100 100 estion Help: Message instructor The position of a pendulum at any given time is represented by the angle, 0 1. The angle is measured from the vertical, which is an imaginary line that is perpendicular to the ground, shown by the dashed line in the figure. When the spherical weight is to the left of the vertical, 0 is positive, and when the spherical weight is to the right of the vertical, 0 is negative. The angle of a pendulum is a function of time, and is given by the following equation Note : The variable t is not underneath the square root symbol . " The Greek letter theta , 0 , is used often in science and engineering to represent an angle . B (1) = Bocos ( Vi') Suppose that the values of \\theta_0'; 8, and L' for a particular pendulum are such that the where equation that models the motion of the pendulum is go is the intial angle measured in radians, of the pendulum just before it is released. When the spherical "theta(t ) = \\cost weight starts to the left of the vertical, 0 is positive, and when the spherical weight starts to the right of the vertical , 0 is negative . re, this is calle cake for the pendulum to complete o ack-and-forth" cycle? As we have g is the acceleration due to Earth's gravity (9.81 32 ) Hint L is the length of the pendulum, in meters. Answer: seconds part bittheme second is referred to as here d its frequency. The What is the frequency of the pendulum? Rou swer to three decimal places. Hint art D: On the following set of axes, graph the vertical displacement of the masss, (t) from t = Answer: Consider an antenna that is 3 m long and has a 5.1 kg mass at its end. RF2_4A_Practice los Q05 01 045 02 025 03 0.35 04 Score: 0/6 0/1 answered The geometry and materials of the beam result in a value of C = 2.31 x 105 28. The mass is given an initial downward vertical displacement of 0.1 m and then released. - 0.os . Question 1 Part A: Write the equation of the vertical displacement of the mass as a function of time, y(t) after sticking horizontally out of a building . parallel to the re is called a cantilever beam. An example of cantilever be sa flagpole leased. Round the coefficient of t inside the cosine function to two places. y (t ) = Clear All Draw : MW flagpole will bounce up and could bend the pole by some in roun when the bird me when the cap on the end is vertically displaced by an initial amount yoke. the equation that describes its motion is similar to Part B: What is the period of the oscillations of agpole? Round your answer to three decimal Part E: If the initial vertical displacement is changed to yo = 0.15m write the equ ation for y(t) and graph the vertical displacement of the mass, y(t), below. Answer : seconds y(t) = it is the time, in seconds, since the flagpole began o CC is determined by the geome which it is made ; LL is the length of the flagpole, in places Part C: What is the frequency of the oscillations of the flagpole?Round your answer to two decimal MM is the mass of the cap at the end of the flagpole, in kilograms; You is the initial vertical displacement of the end of the flagpole, in meters. Answer: The motion of the flagpole is similar to that of a pendulum in that it oscillates ab downwards, of the end of the flagpole. This means that if) tos 0.05 01 0. 15 02 0 25 03 0,35 04 (n) > o, y(t) > 0, the flagpole is bent down; 3 (1) - 0, the flagpole is exactly horizontal; and ()