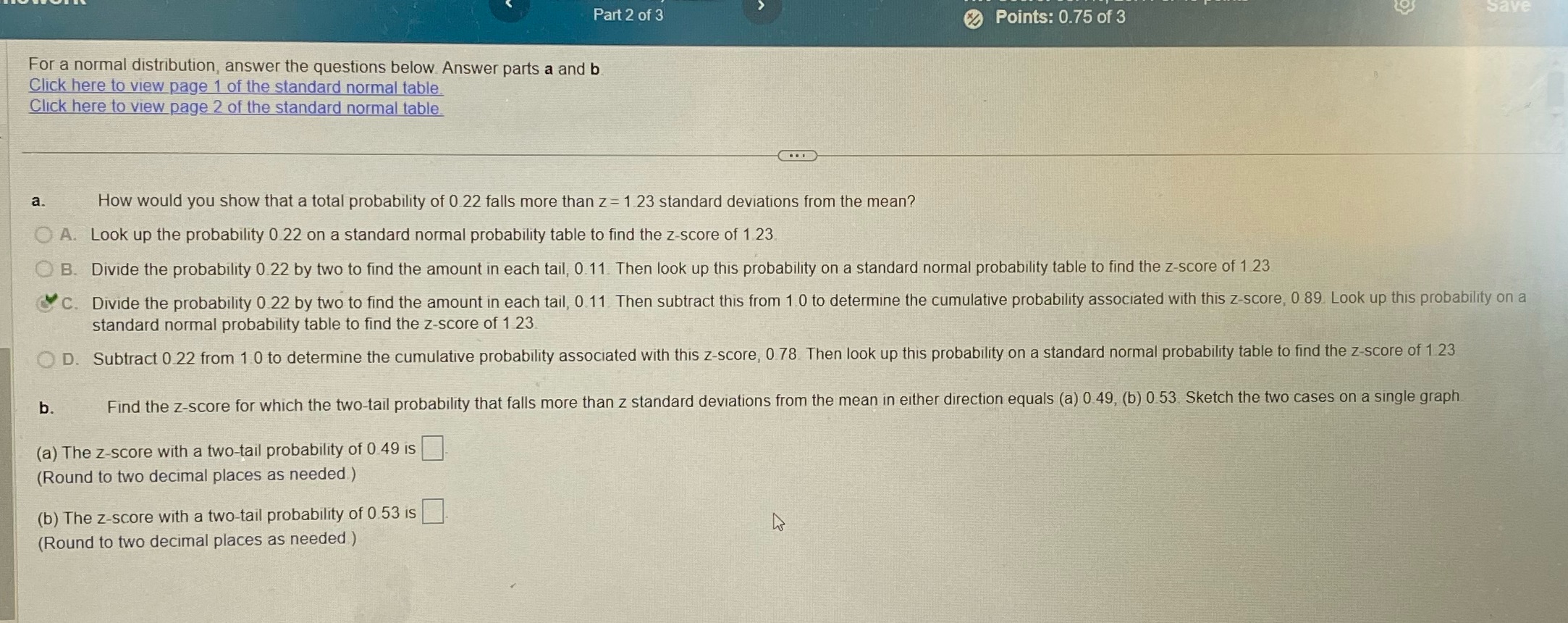
For a normal distribution, answer the questions below. Answer parts a and b Click here to view page 1 of the standard normal table. Click here to view page 2 of the standard normal table. Save Part 2 of 3 Points: 0.75 of 3 a. How would you show that a total probability of 0.22 falls more than z = 1.23 standard deviations from the mean? OA. Look up the probability 0.22 on a standard normal probability table to find the z-score of 1.23 b. B. Divide the probability 0.22 by two to find the amount in each tail, 0.11. Then look up this probability on a standard normal probability table to find the z-score of 1.23 C. Divide the probability 0.22 by two to find the amount in each tail, 0.11 Then subtract this from 1.0 to determine the cumulative probability associated with this z-score, 0.89. Look up this probability on a standard normal probability table to find the z-score of 1.23 D. Subtract 0.22 from 1.0 to determine the cumulative probability associated with this z-score, 0.78. Then look up this probability on a standard normal probability table to find the z-score of 1.23 Find the z-score for which the two-tail probability that falls more than z standard deviations from the mean in either direction equals (a) 0.49, (b) 0.53 Sketch the two cases on a single graph (a) The z-score with a two-tail probability of 0.49 is (Round to two decimal places as needed.) (b) The z-score with a two-tail probability of 0.53 is (Round to two decimal places as needed)