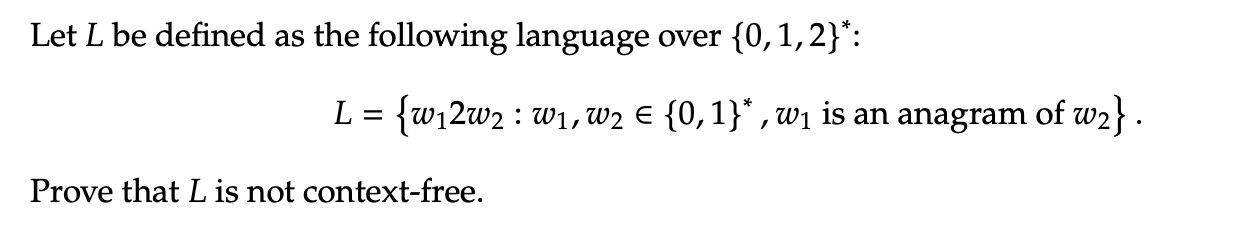
For a Turing machine M, (M) refers to the binary representation of M. For a Turing machine M, L(M) contains the set of all strings accepted by M. For a Turing machine M and an input x {0,1}*, Steps(M, x) refers to the number of steps taken by M to execute on x before it halts. Here, one step of execution of M on x = one movement (left or right) of the tape head. For a Turing machine M and an input x {0, 1}*, we define the following: ReachCells(M, x) = {i : M reaches ith tape cell when M is executed on x} Informally, it contains all locations on the tape that are visited when M is ecuted on x. The leftmost location on the tape is the first tape cell, the location next to it is the second tape cell, and so on. A string w is an anagram of w2 if w can be obtained by rearranging the alphabets of w2. Formally, if w is an n length string, w is called an anagram of w if there exists a permutation on n elements such that (w) = W2. Let L be defined as the following language over {0, 1,2}*: L = {w2w2 : W, W {0, 1}*, w is an anagram of w} . Prove that L is not context-free.