For an preliminary funding of one hundred, an funding yields returns of Xi on the cease of duration i for i = 1, 2, in which X1 and X2 are impartial everyday random variables with mean 60 and variance 25. What is the opportunity the price of return of this funding is more than 10 percent? Exercise four.29 The inflation charge is described to be the fee at which prices as a whole are growing. For example, if the every year inflation charge is four% then what cost $a hundred closing yr will value $104 this yr. Let ri denote the inflation price, and keep in mind an funding whose price of go back is r. We are regularly interested by determining the funding's rate of go back from the factor of view of ways lots the investment increases one's pur- chasing energy; we call this quantity the funding's inflation-adjusted price of go back and denote it as ra. Since the shopping power of the quantity (1 + r)x three hundred and sixty five days from now's equivalent to that of the quantity (1 + r)x/(1 + ri) today, it follows that - with admire to consistent pur- chasing energy gadgets - the investment transforms (in a single term) the quantity x into the quantity (1+r)x/(1+ri). Consequently, its inflation- adjusted fee of return is ra = 1 + r 1 + ri ? 1. When r and ri are each small, we've the following approximation: ra ? r ? ri .

Suppose that the nominal interest price is r, and keep in mind the following version for pricing an choice to purchase a stock at a future time at a hard and fast fee. Let the prevailing price (in greenbacks) of the inventory be a hundred in step with share, and think we know that, after one term, its rate will be either 200 or 50 (see Figure 5.1). Suppose in addition that, for any y, at a cost of Cy you should buy at time 0 the choice to shop for y stocks of the stock at time 1 at a fee of a hundred and fifty per proportion. Thus, as an example, if you purchase this option and the inventory rises to 2 hundred, then you could exercising the op- tion at time 1 and comprehend a advantage of 200 ? 150 = 50 for every of the y options bought. On the alternative hand, if the rate of the stock at time 1 is 50 then the option might be worthless. In addition to the options, you may also purchase x stocks of the inventory at time 0 at a price of 100x, and every share could be well worth both 2 hundred or 50 at time 1. We will think that both x and y may be positive, poor, or zero. That is, you could either buy or sell both the stock and the choice. For in- stance, if x were terrible then you definately might be selling ?x stocks of inventory, yielding you an preliminary return of ?100x, and you'll then be responsi- ble for buying and returning ?x stocks of the inventory at time 1 at a (time-1) cost of either 200 or 50 consistent with share. (When you promote a inventory that you do no longer personal, we are saying that you are selling it short.) We are interested in figuring out the ideal value of C, the unit fee of an option. Specifically, we will show that if r is the one-period hobby rate then, except C = [100 ? 50(1 + r)?1 ]/three, there may be a com- bination of purchases a good way to continually result in a superb gift cost gain. To display this, think that at time 0 we buy x units of inventory

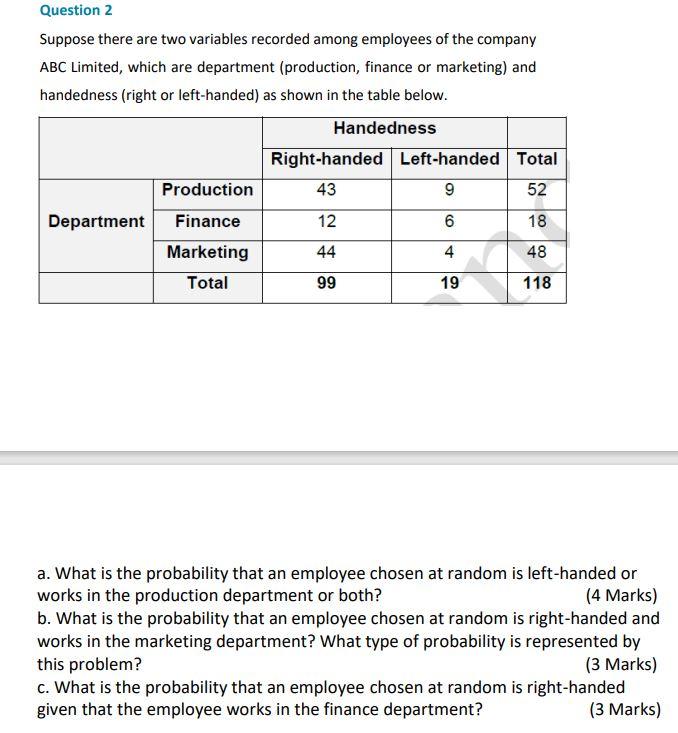
QUESTION 1

A standard normal density is a probability density function for a random variable that is normally distributed with population mean = 0 and population variance = 1. Using a table of standard normal probabilities, such as Table A1 in your textbook, answer the following questions: a) If a random variable has a standard normal density, what is the probability that this random variable is less than 1.5? b) If a random variable has a standard normal density, what is the probability that this random variable is less than -2.0? c) If a random variable has a standard normal density, what is the probability that this random variable is between -2.0 and 1.5? d) Find the 68% critical value for a random variable that has a standard normal density.