For both questions below, consider the causal coupled-form all-pole filter shown in Fig. 1 with transfer function

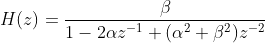
(a). Suppose we wish to realize the transfer function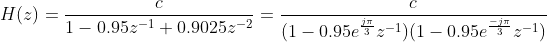

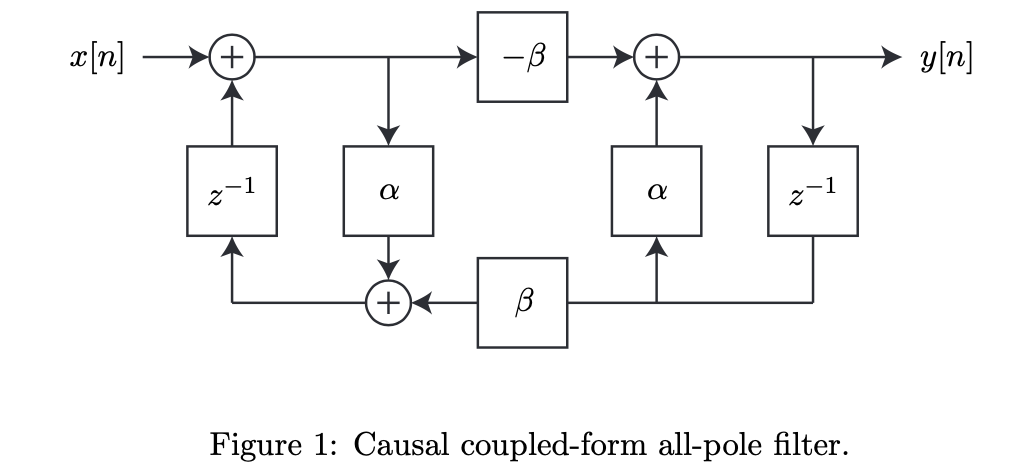
for some positive constant c. Solve for and such that this transfer function is realized in the coupled-form shown in Fig. 1.

MY ANSWER: 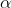= 0.475 and =0.8227. Please feel free to use these numbers or calculate to double check, then solve part B.

(b). Use your (unquantized) values for and from problem (a) and assume all non-unity products in this realization are immediately rounded before any additions are done. Insert round-off noise sources at appropriate locations in the coupled-form flow-graph of Fig. 1 to model the effect of the rounding error. Assuming each multiplier generates independent rounding error noise with variance ²_B, compute the total noise power at the output. Your answer should be in the form ²_y = ²_B for some positive value of .

Please answer both parts, thank you!

[n] + -B + yn a a z + B Figure 1: Causal coupled-form all-pole filter. H(-) = j 1- 0.952-1 + 0.90252-2 (1 0.95e-z-1)(1 0.95e-72-1) [n] + -B + yn a a z + B Figure 1: Causal coupled-form all-pole filter. H(-) = j 1- 0.952-1 + 0.90252-2 (1 0.95e-z-1)(1 0.95e-72-1)