For part a, this is what I've tried:

4a)

sinx = d/(2/L) = d/2L

T_1sinx - mg = 0
T_1sinx = mg


T_1(d/2L) = mg

T_1 = 2mgL/d

How do I go about proving what needs to be shown? What logic needs to be used here? I am aware the forces must be in equilibrium, but how can you work with the horizontal ones since it's just leading you to more unknowns i.e F = mv^2/r?

4b) For angular Velcoity, I am aware we would use w = theta/t however how do you even consider starting with this proof?

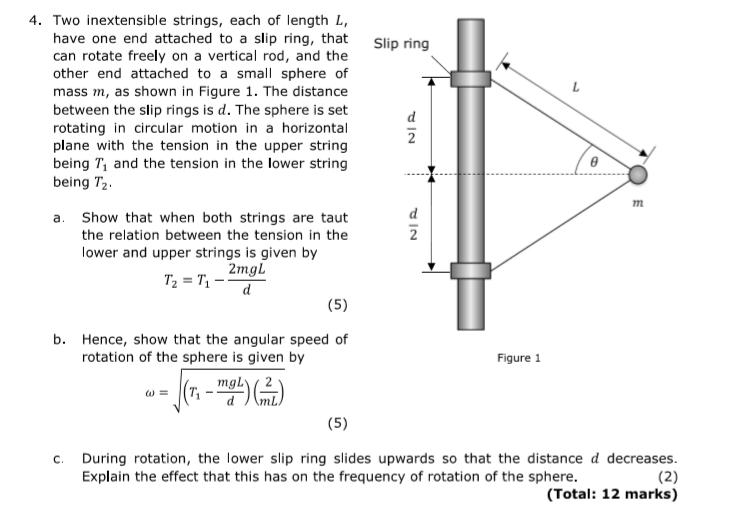
4. Two inextensible strings, each of length L, have one end attached to a slip ring, that can rotate freely on a vertical rod, and the other end attached to a small sphere of mass m, as shown in Figure 1. The distance between the slip rings is d. The sphere is set rotating in circular motion in a horizontal plane with the tension in the upper string being T1 and the tension in the lower string being T2. Slip ring Show that when both strings are taut the relation between the tension in the a. lower and upper strings is given by 2mgL T2 = T1-d (5) b. Hence, show that the angular speed of rotation of the sphere is given by Figure 1 mgLy %3D (5) During rotation, the lower slip ring slides upwards so that the distance d decreases. (2) (Total: 12 marks) C. Explain the effect that this has on the frequency of rotation of the sphere.