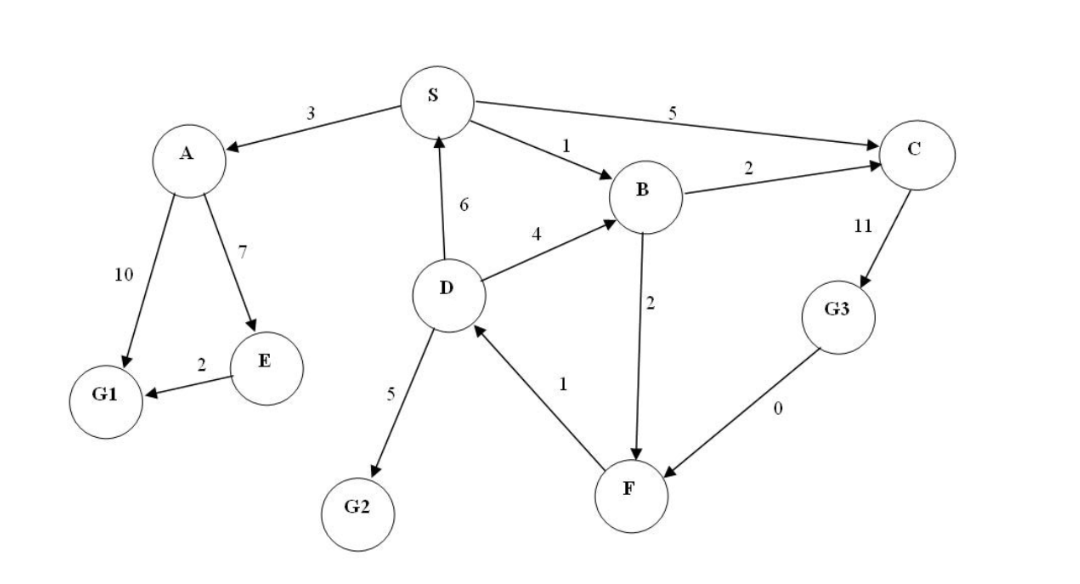
For the graph shown in Figure 1, assume S is the start state and G1, G2, and G3 are goal states. The numbers on the edges represent cost and the arrows represent the direction in which an agent can move (For example, an agent can move from S to A but not vice-versa). Consider the problem where an agent is at the start state and needs to reach one of the goal states. Simulate the search algorithms: Breadth-first Search, Depth-first Search, Uniform 2 Cost Search, and Depth-limited search with a depth limit 2, and answer the following for each search algorithm:

1. What is the goal state that is achieved and the cost of the path to reach to the goal state?

2. List the order of the states that are popped in the POP() functions in Figures 3.9 and 3.12.

Fig3.9:

fig 3.12:

3. Has the search algorithm chosen the optimal path to reach the goal state that it ended up in (i.e., your answer for part 1)? 4. Has the algorithm chosen the goal state that leads to the optimal path? If yes, has it chosen the optimal path to reach this state?

function BREADTH-FIRST-SEARCH ( problem) returns a solution node or failure node NodE(problem.INITIAL) if problem.IS-GOAL (node.STATE) then return node frontier a FIFO queue, with node as an element reached { problem.INITIAL } while not IS-EMPTY (frontier) do node POP( frontier ) for each child in EXPAND(problem, node) do s child.STATE if problem.IS-GoAL (s) then return child if s is not in reached then add s to reached add child to frontier return failure function UNIFORM-COST-SEARCH ( problem) returns a solution node, or failure return BEST-FIRST-SEARCH(problem, ATH-COST) function ITERATIVE-DEEPENING-SEARCH(problem ) returns a solution node or failure for depth =0 to do result DEPTH-LIMITED-SEARCH ( problem, depth) if result = cutoff then return result function DEPTH-LIMITED-SEARCH(problem, ) returns a node or failure or cutoff frontier a LIFO queue (stack) with NODE (problem.INITIAL) as an element result failure while not IS-EMPTY(frontier) do node POP( frontier ) if problem.IS-GOAL(node.STATE) then return node if DEPTH( node )> then result cutoff else if not IS-CYCLE(node) do for each child in EXPAND(problem, node) do add child to frontier