For these two python classes, only do the findEuler and tryVisiting method in Graph.py

Here is Graph.py

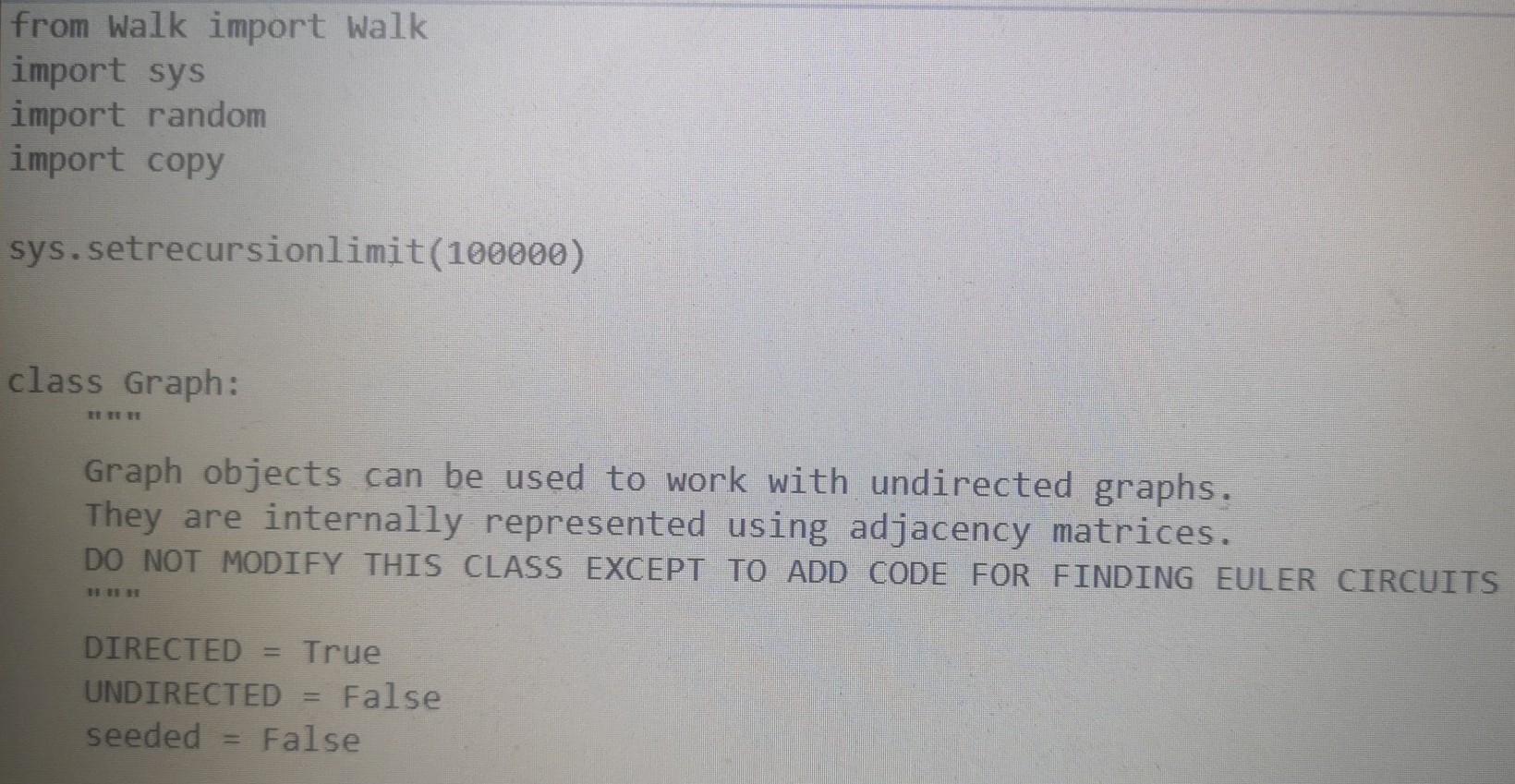
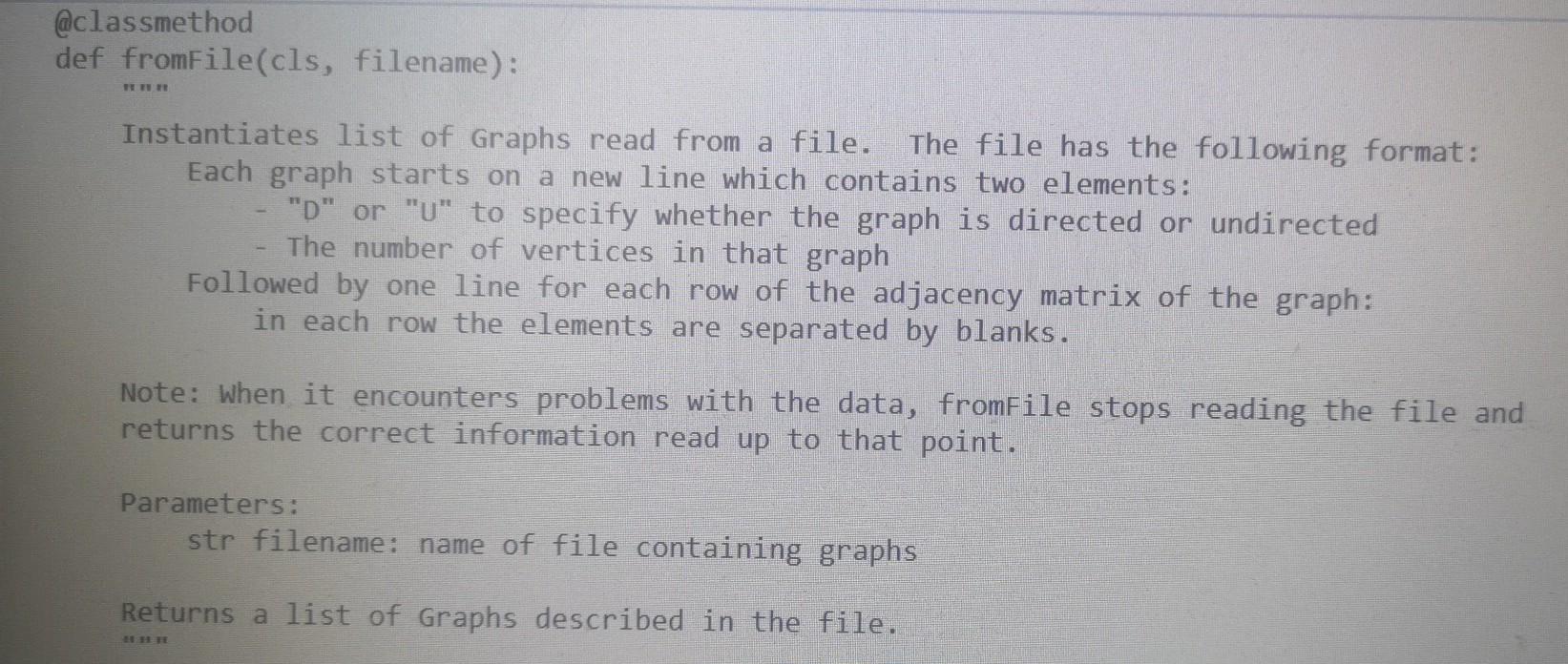
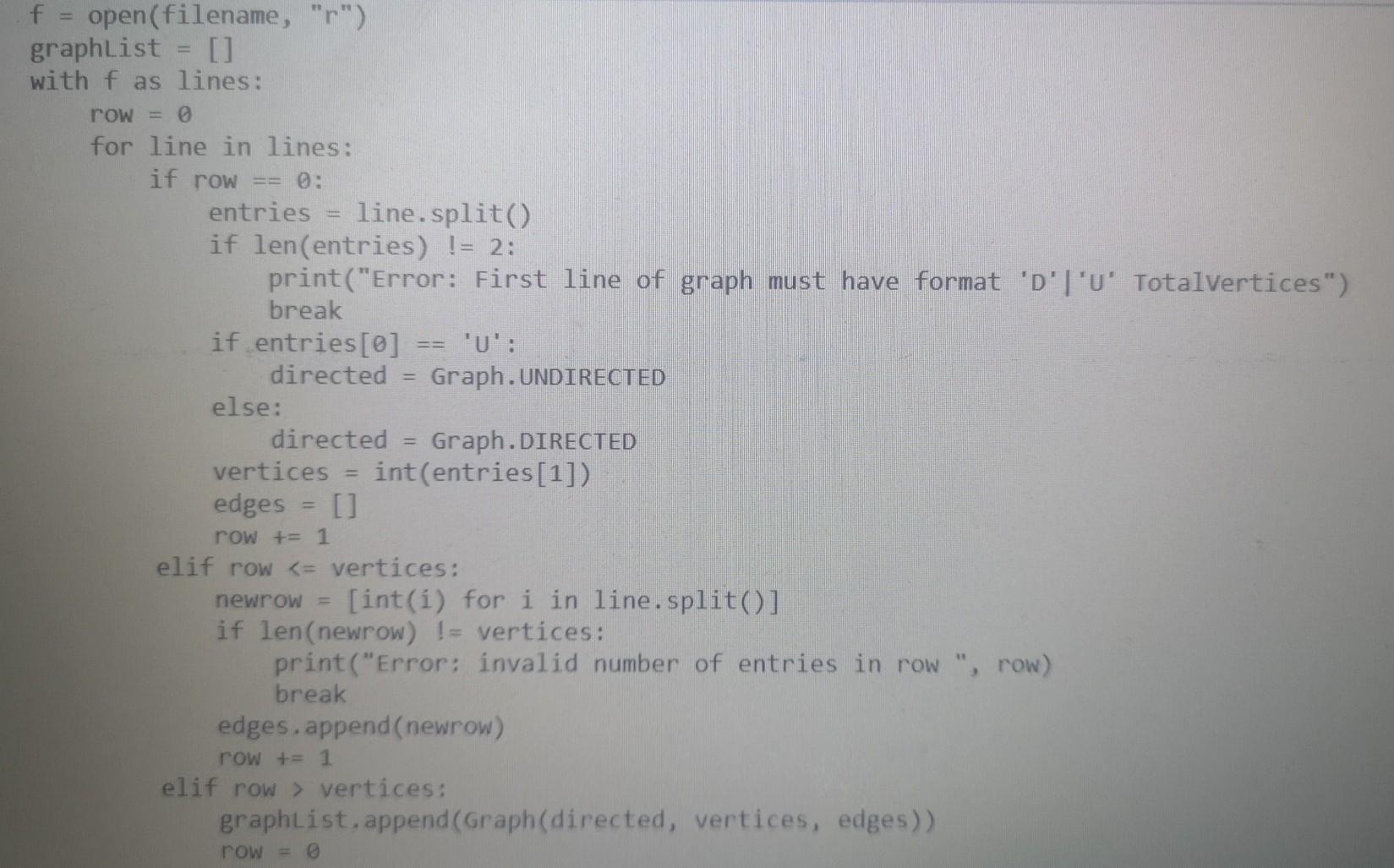
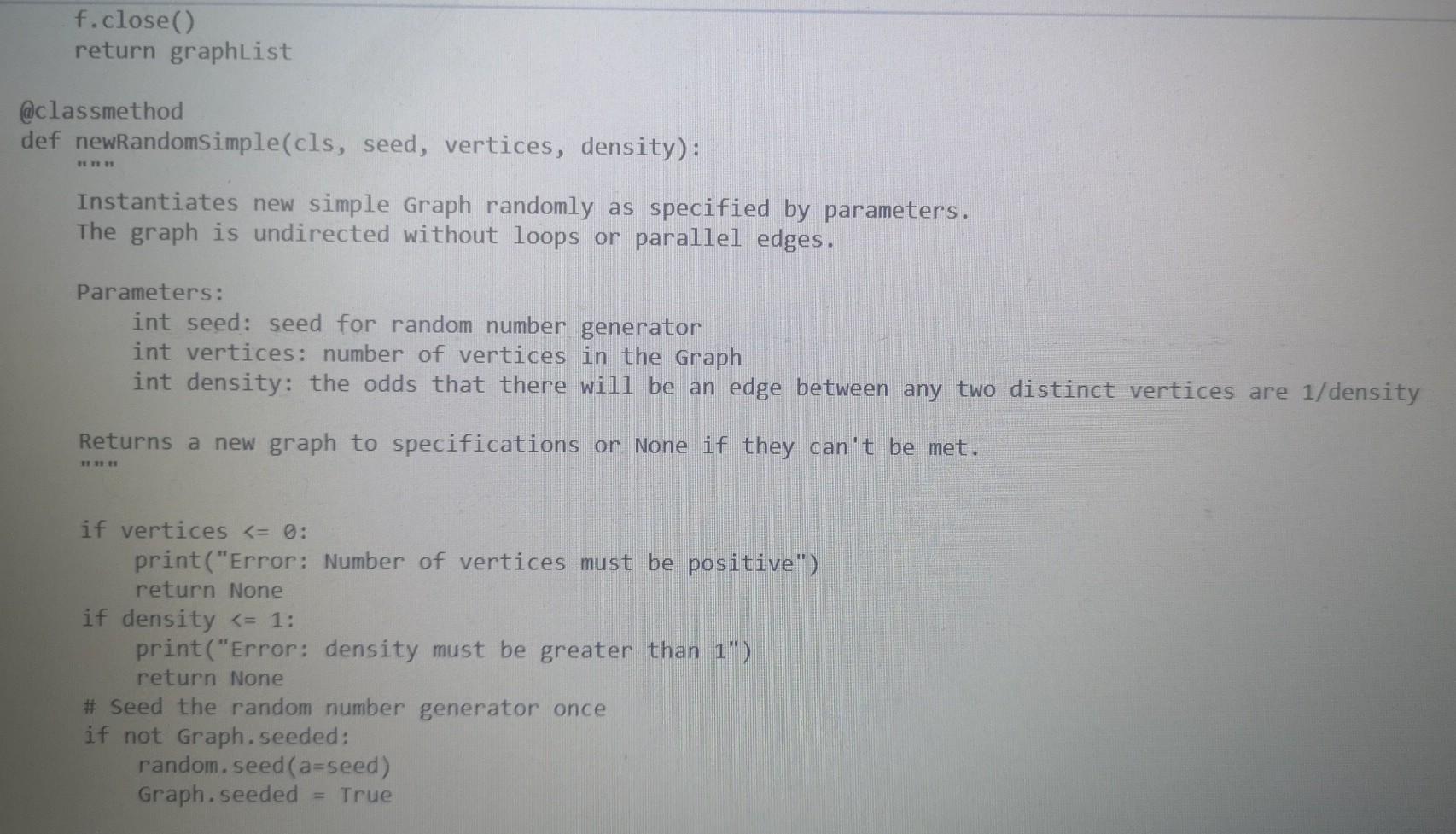
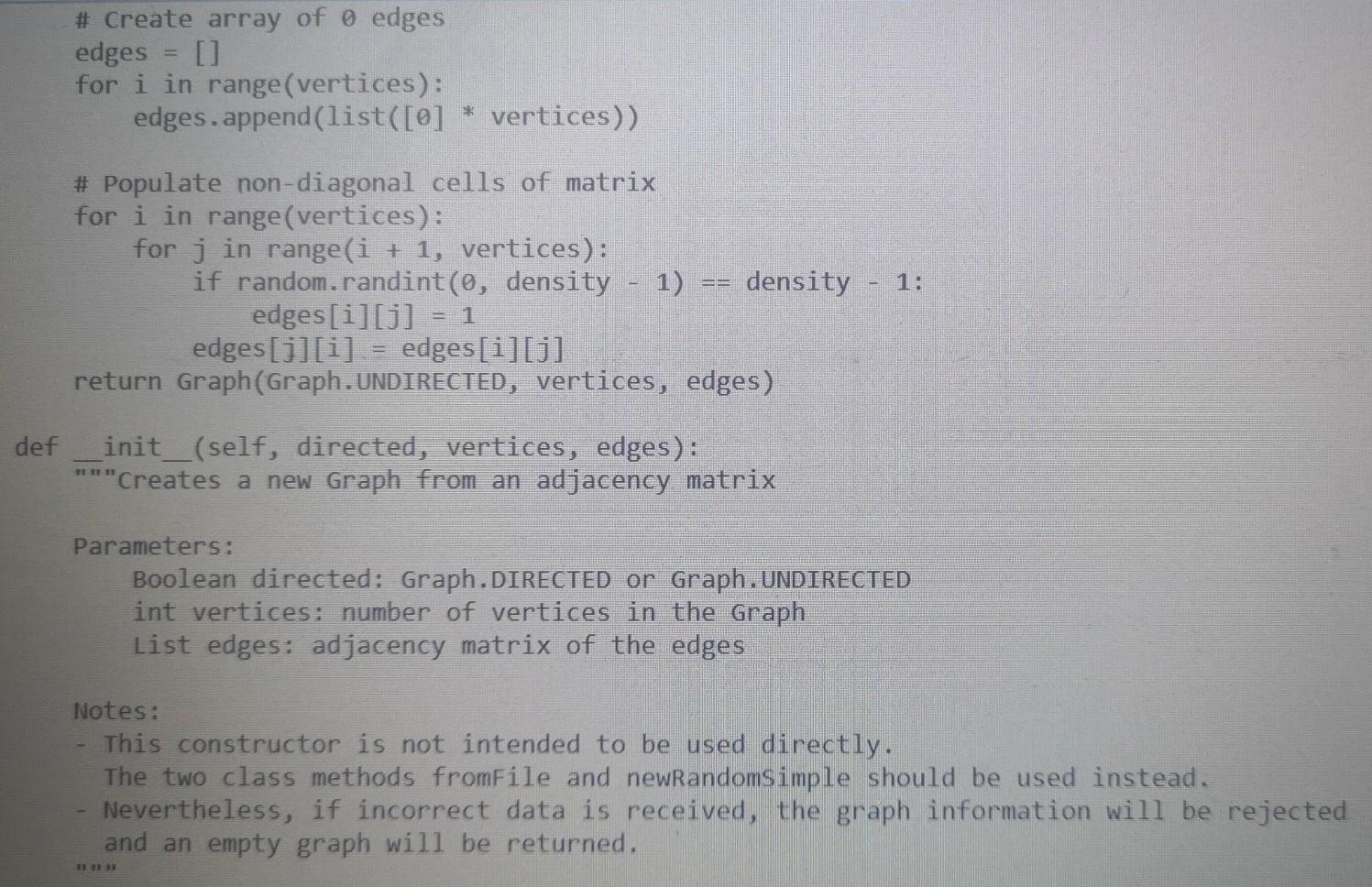
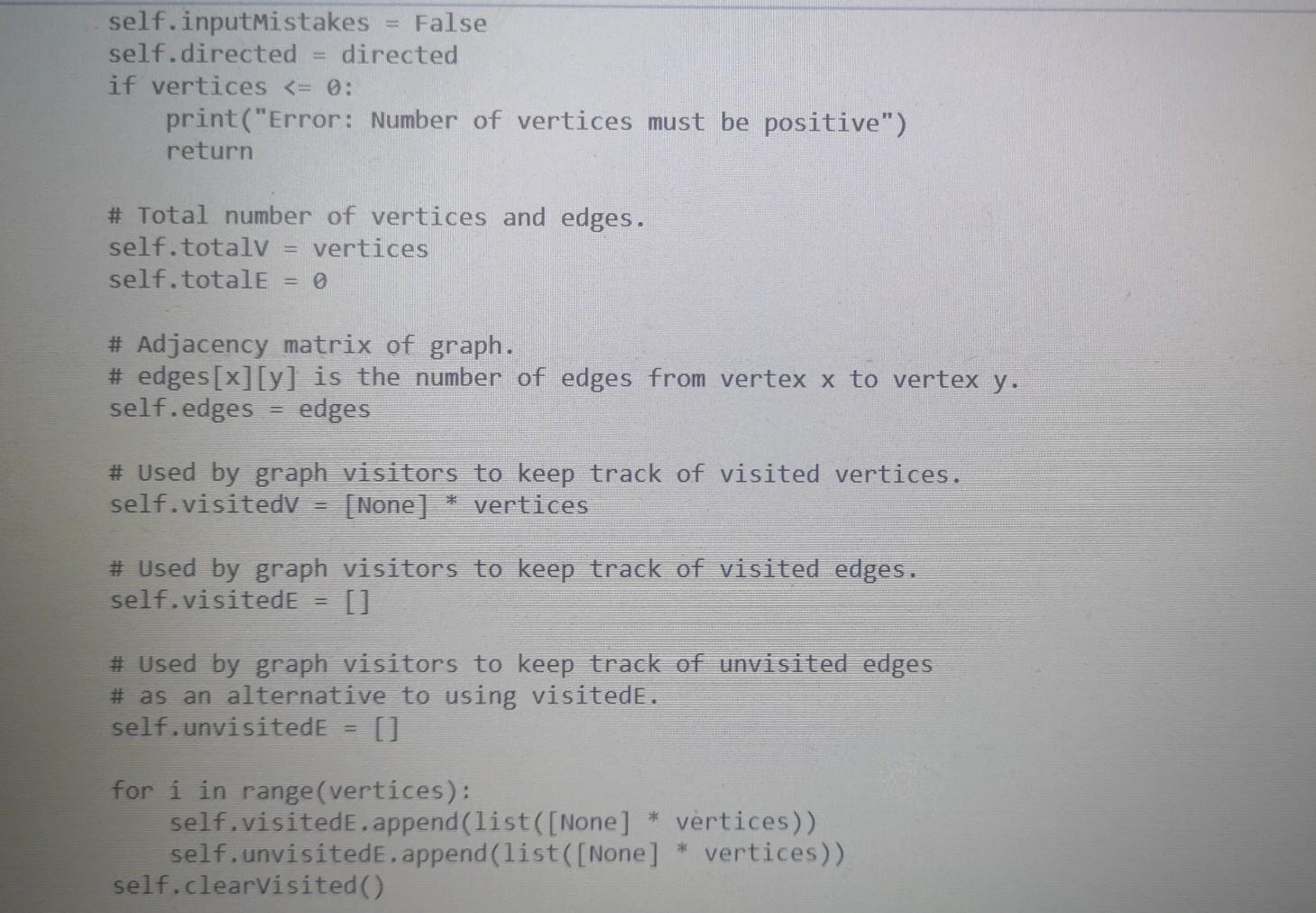
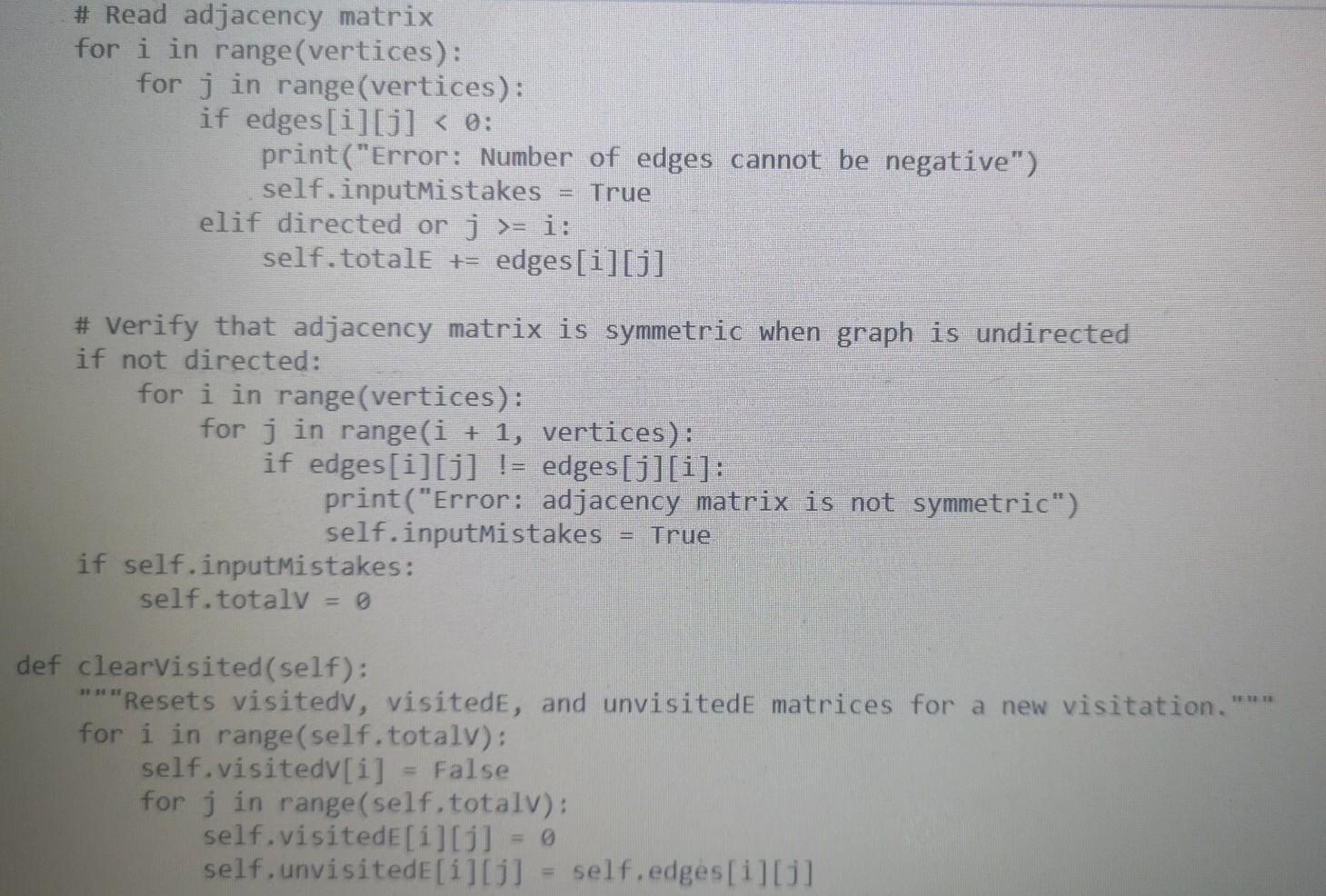
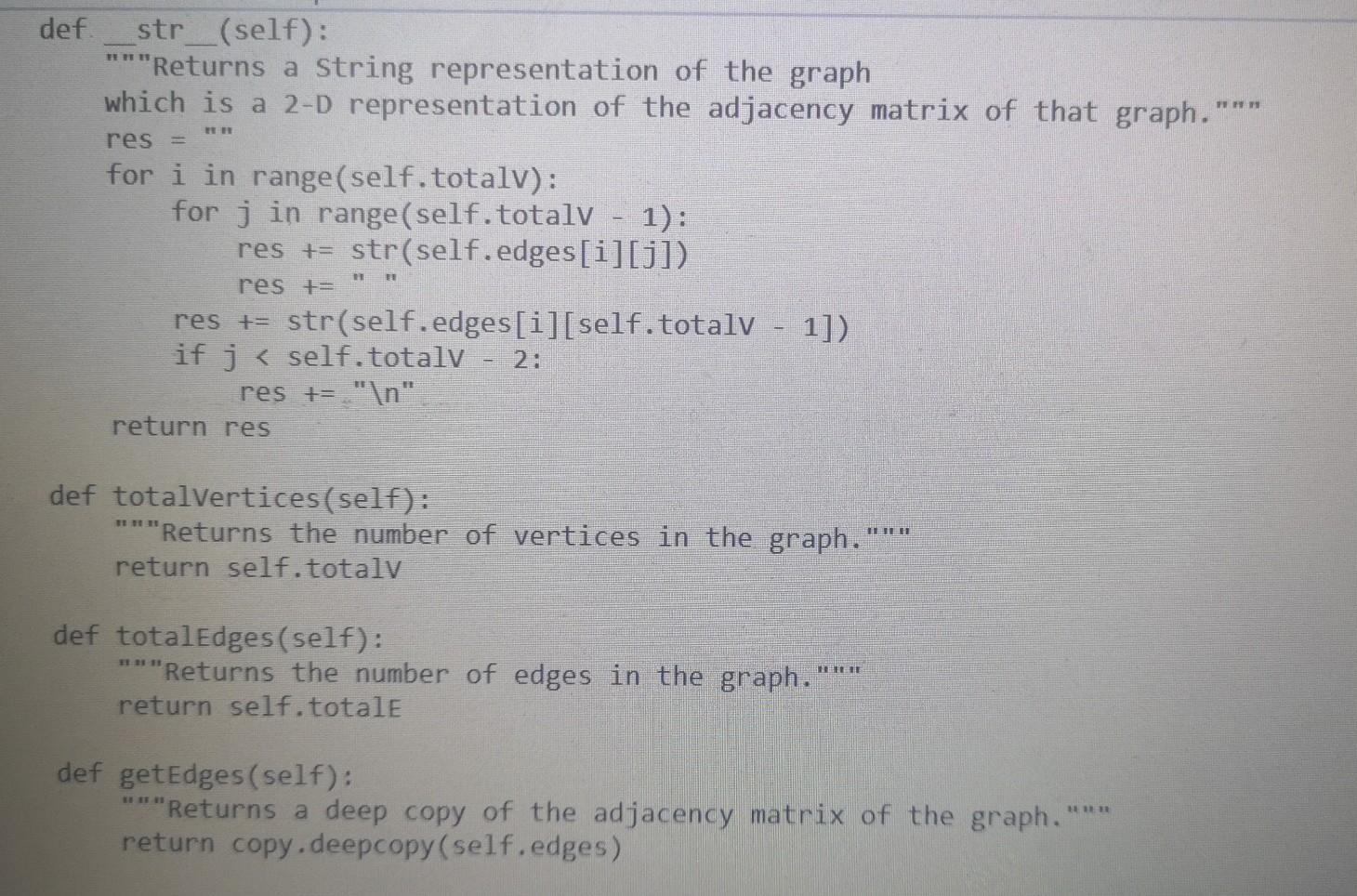
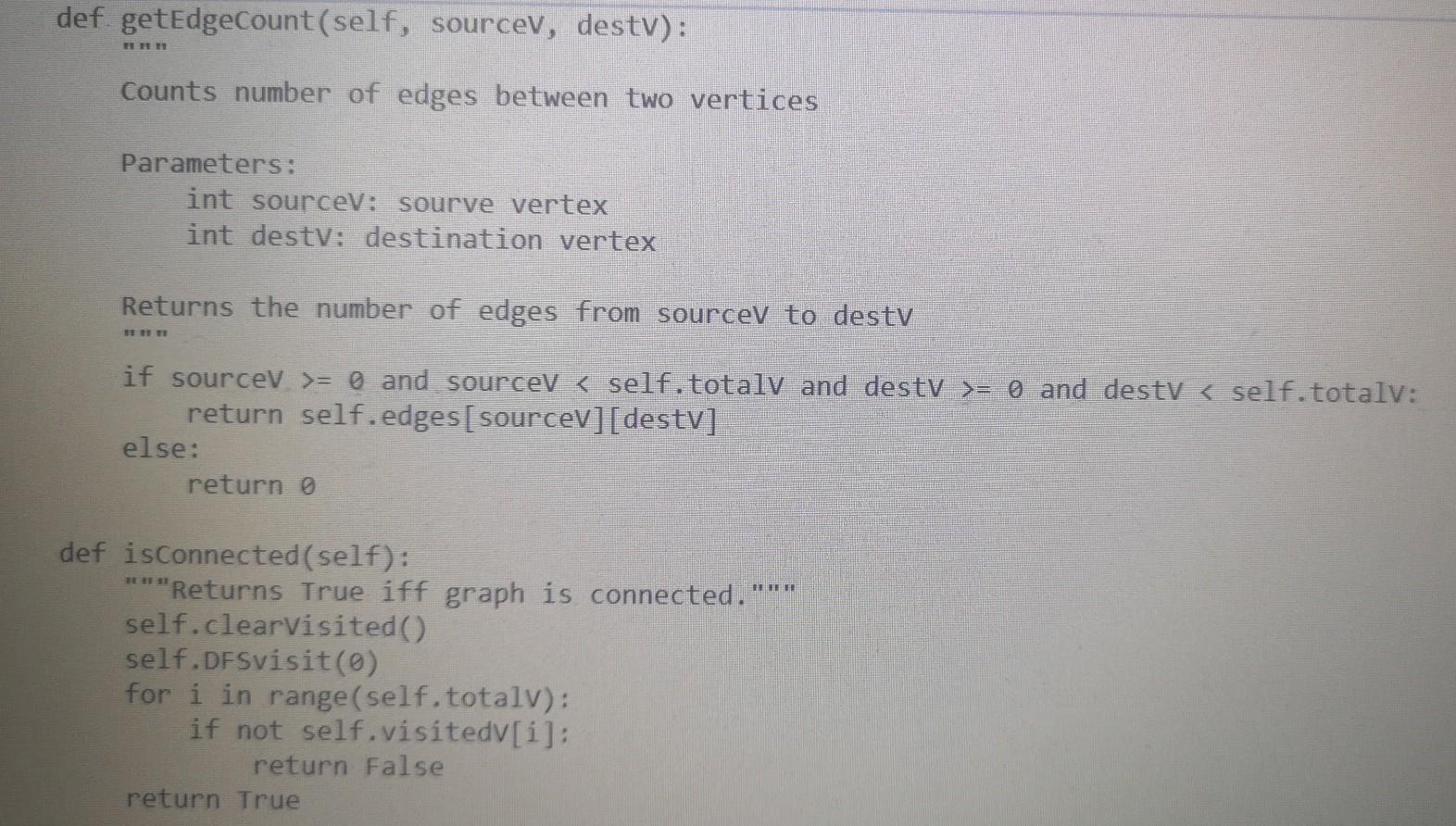
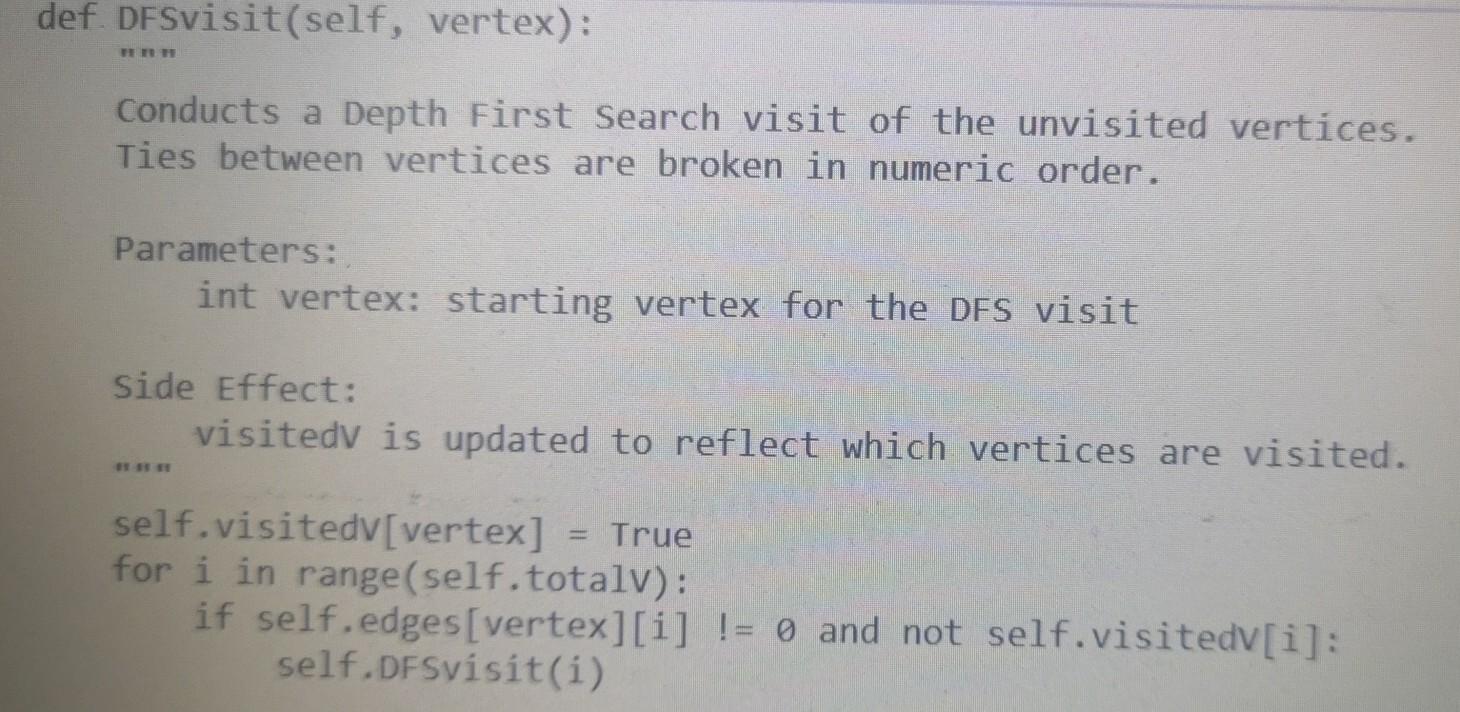
Here is Walk.py

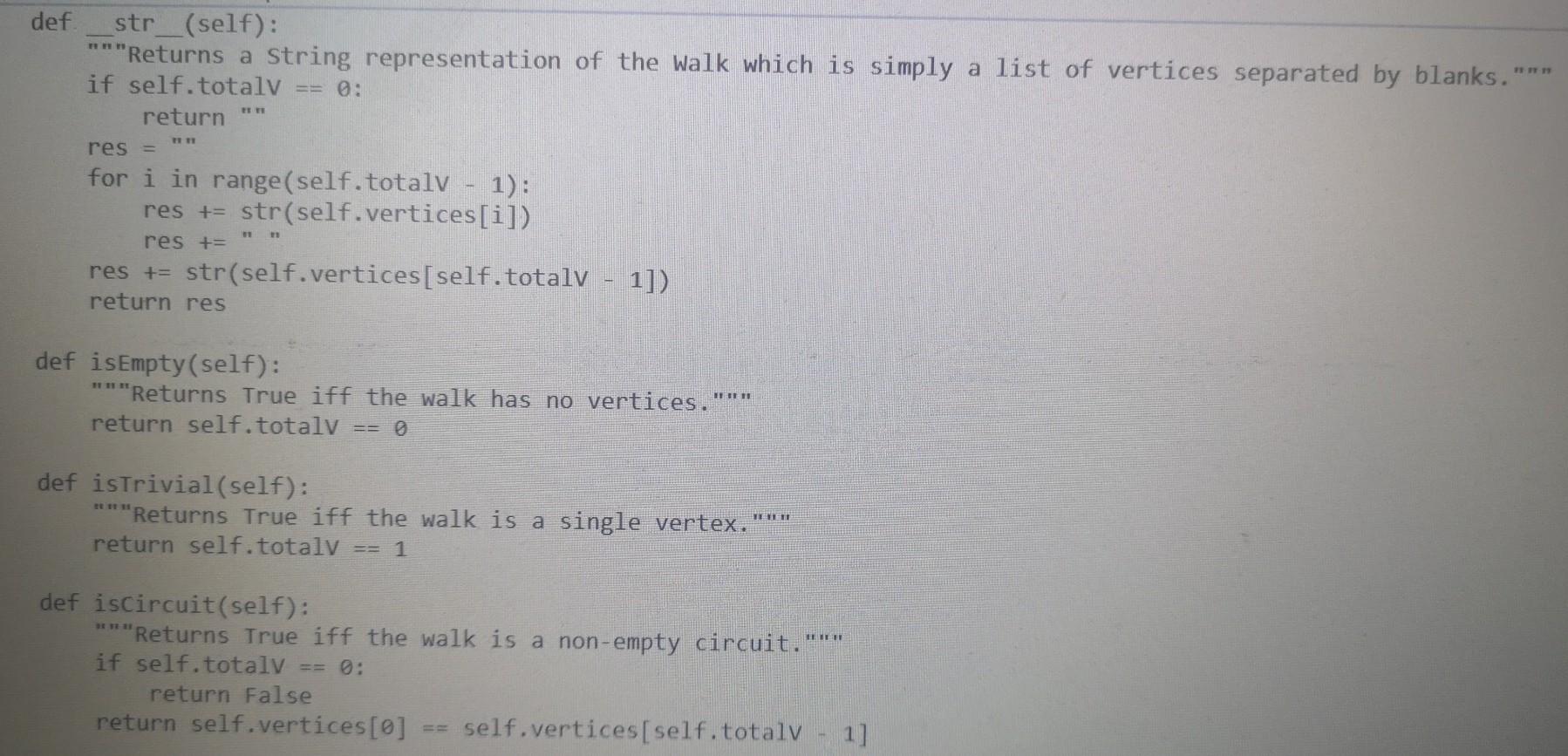
from Walk import Walk import sys import random import copy sys.setrecursionlimit(100000) class Graph: Graph objects can be used to work with undirected graphs. They are internally represented using adjacency matrices. DO NOT MODIFY THIS CLASS EXCEPT TO ADD CODE FOR FINDING EULER CIRCUITS DIRECTED True UNDIRECTED False seeded False @classmethod def fromFile(cls, filename): Instantiates list of Graphs read from a file. The file has the following format: Each graph starts on a new line which contains two elements: "D" or "U" to specify whether the graph is directed or undirected The number of vertices in that graph Followed by one line for each row of the adjacency matrix of the graph: in each row the elements are separated by blanks. Note: When it encounters problems with the data, fromFile stops reading the file and returns the correct information read up to that point. Parameters: str filename: name of file containing graphs Returns a list of Graphs described in the file. f = open(filename, "r") graphList [] with f as lines: row = 0 for line in lines: if row == 0: entries line.split() if len(entries) != 2: print("Error: First line of graph must have format 'D'I'U' Totalvertices") break if entries[0] directed = Graph. UNDIRECTED else: directed = Graph.DIRECTED vertices int(entries[1]) edges = [] row += 1 elif row vertices: graphList.append(Graph(directed, vertices, edges)) row = 6 f.close() return graphList @classmethod def newRandomSimple(cls, seed, vertices, density): HET Instantiates new simple Graph randomly as specified by parameters. The graph is undirected without loops or parallel edges. Parameters: int seed: seed for random number generator int vertices: number of vertices in the Graph int density: the odds that there will be an edge between any two distinct vertices are 1/density Returns a new graph to specifications or None if they can't be met. if vertices = i: self. totale += edges[i][j] True # Verify that adjacency matrix is symmetric when graph is undirected if not directed: for i in range(vertices): for j in range(i + 1, vertices): if edges[i][j] != edges[j][i]: print("Error: adjacency matrix is not symmetric") self.inputMistakes True if self.inputmistakes: self. totaly def clearvisited(self): "Resets visitedv, visitede, and unvisitede matrices for a new visitation." for i in range(self.totalv): self.visitedv[i] = False for j in range(self.totalv): self.visitede[i][j] self.unvisited[i][j] = self.edges[i][j] def str_(self): "Returns a string representation of the graph which is a 2-D representation of the adjacency matrix of that graph. TY res for i in range(self.totalv): for j in range(self.totalv 1): res += str(self.edges[i][j]) res += 1]) res += str(self.edges[i][self. totalv if j = 0 and sourcev = 0 and desty vertices: graphList.append(Graph(directed, vertices, edges)) row = 6 f.close() return graphList @classmethod def newRandomSimple(cls, seed, vertices, density): HET Instantiates new simple Graph randomly as specified by parameters. The graph is undirected without loops or parallel edges. Parameters: int seed: seed for random number generator int vertices: number of vertices in the Graph int density: the odds that there will be an edge between any two distinct vertices are 1/density Returns a new graph to specifications or None if they can't be met. if vertices = i: self. totale += edges[i][j] True # Verify that adjacency matrix is symmetric when graph is undirected if not directed: for i in range(vertices): for j in range(i + 1, vertices): if edges[i][j] != edges[j][i]: print("Error: adjacency matrix is not symmetric") self.inputMistakes True if self.inputmistakes: self. totaly def clearvisited(self): "Resets visitedv, visitede, and unvisitede matrices for a new visitation." for i in range(self.totalv): self.visitedv[i] = False for j in range(self.totalv): self.visitede[i][j] self.unvisited[i][j] = self.edges[i][j] def str_(self): "Returns a string representation of the graph which is a 2-D representation of the adjacency matrix of that graph. TY res for i in range(self.totalv): for j in range(self.totalv 1): res += str(self.edges[i][j]) res += 1]) res += str(self.edges[i][self. totalv if j = 0 and sourcev = 0 and desty