• Formulas to use to solve the questions below. And use exactly the same formulas as they are in the images below. Same letters and variables in the formulas should be used to solve the problems please. And not any other formulas apart from these should be used to solve the questions please:

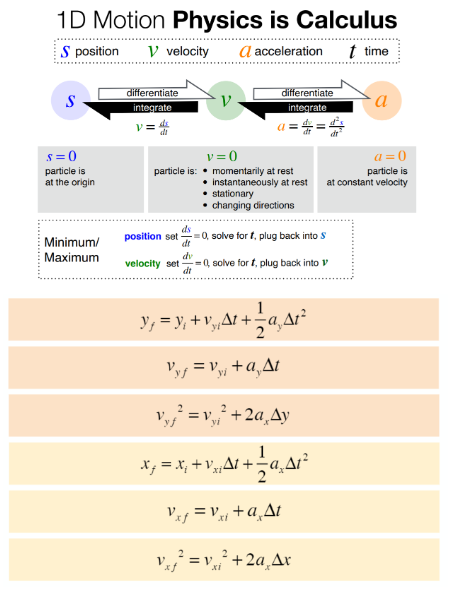
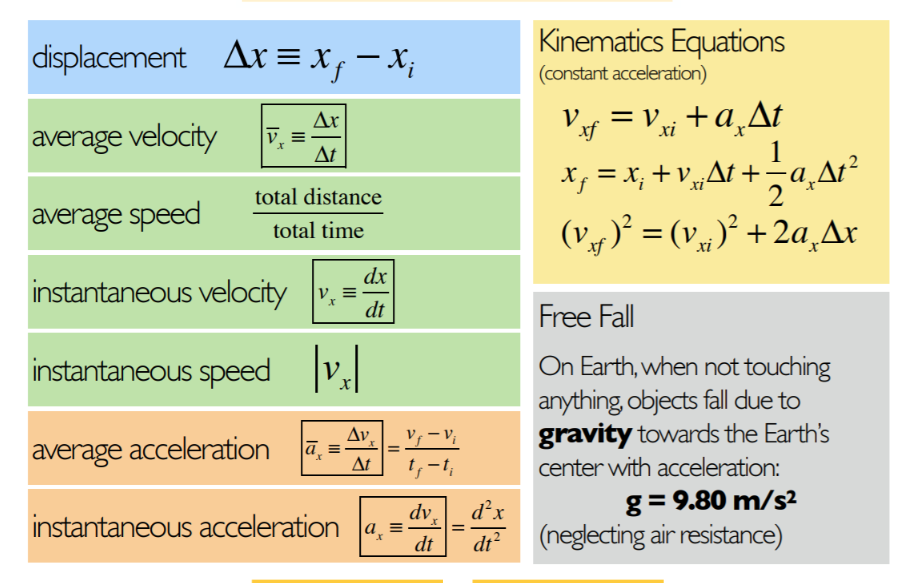
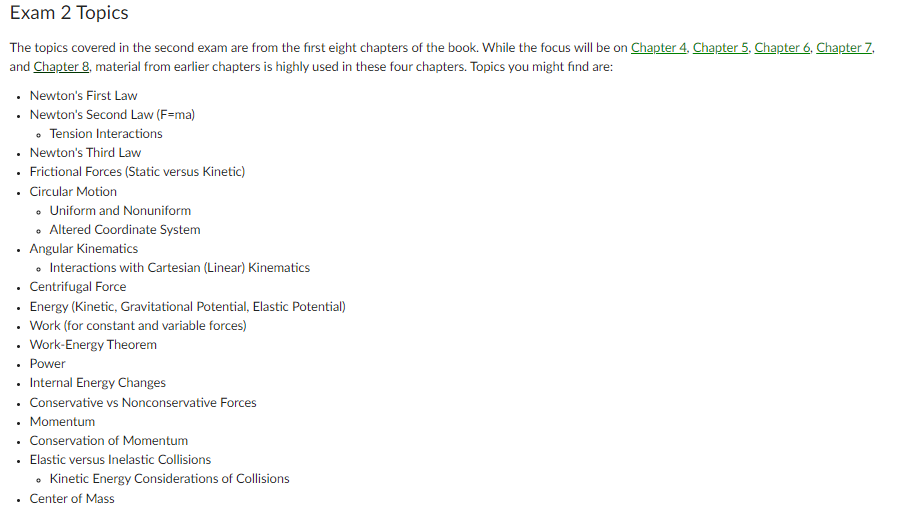
Equation Hub Unit 2 Equations Chapter 4: This chapter is all about properly using Newton's Three Laws F = ma | F, = ma = -mg | FAB = -FBA Chapter 5: Circular motion equations were removed to avoid confusion (slide below) fs,max = As FN If = MFN ID = CopAu I verm = V Amg E F = ma, = = mwrl E F = mat = mor | CF = 0 Chapter 6: Work is a transfer of energy; it has the units of energy W=F . AT = FArcos (@) | W = [" F . di | Fy = -kAs Went = Ky - K = AK |PE dEs _ dW P = F . J d't Chapter 7: The differences in the work equation come from conservative and nonconservative forces Emech = K + UIU, = mgh |Up = ,kx' | Fop = - kx | Emech = AK + AU = 0 F= - UAEin = fAs| W = AK + AU + AEint Chapter 8: Collision equations have not been given here. Just the general form. p = mulp = p/ IF = #|Ap = FagAt = J|J = ff Fat | P = pa + pi + pet ... = mova + moun + movet... To =Ema, = mintmint. | Cem = 4 fadm | of - vi = Veln (M) Graphics from Slides: Here are several still images from slides of different useful equations.Free Body Diagrams Identify the different forces acting on a particle Represent the object as a particle at the center of a coordinate system Draw each force as a vector pointing in the correct direction If possible, identify the direction of the net force Uniform Circular Motion object moves with constant (tangential) speed Speed T 2nt Rf a. Centripetal Acceleration a = R Centripetal Force EF, =mui REssential concepts Particle acceleration, force, interaction Basic Goals How does a particle respond to a force? How do objects interact? Newton's First Law AV =0- a=0-F =0 General Principles Newton's Second Law F = ma Newton's Third Law FAOn B = - FBon A Basic Problem Solving Strategy Linear Motion Trajectory Motion Circular Motion F. = max F. =0 SF = ma, SF, = ma, = = mor SF =0 F. = may SF, = ma, EF, = ma, EF. = ma. Linear & Trajectory Kinematics Circular Kinematics General Case Uniform Acceleration: T = Uniform V v. = v + alt Circular Motion: 0, =0,+wAt V = ds -= slope of position graph as = constant As = v.At + ya(At ) V, = Or dy= slope of velocity graph v? = v2+2als dt W =W, +aAt Av = [a dt = area under acceleration curve Uniform Motion: Nonuniform 40 = 0,At + ya(At ) As = [v dt = area under velocity curve a, =0 Circular Motion: v, = constant As = v.At w =0, +2040Unit 1 Equations Chapter 1: This chapter was setting up the math. Familiarity with vectors is big here A . B = B . A= |AB cos(0) | A . B = AB, + AyBy + AB, | AxB = -BX A = [AB sin(0) | Ax B = (A,B. - A,By)i+ (A.B, - AB.) j+ (A.By - A, B.) k Chapter 2: Gradients are for variables that dont change with time, derivatives are for variables that change with time Chapter 3: Several topics didn't have equations, like reference frames and some directions of relative velocity. Its worth looking those parts over. Ar = (Ax)i + (Ay) =raitry)|AT = ry - rix = utta |vang = At Ar dr dy dt -th Qaug E At At la = do Range = " sin ( 20) lac = "pla = " =w'r Graphics from Slides: Here are several still images from slides of different useful equations.1D Motion Physics is Calculus S position V' velocity acceleration time differentiate differentiate S ntograte intograte a V= M 5=0 ( =0 particle is particle is: * momentarily at rest particle is at the origin . instantaneously at rest at constant velocity * stationary * changing directions position set as Minimum/ =0, solve for f, plug back into $ Maximum dv velocity set = 0, solve for f, plug back into v y = y +V Al+ -a At- 2 Vy =V Vyf 2=v + 2a Ay X=X +V Al+-aAt- 2 VIf =Vita At 2 V &f xi 2+2a Axdisplacement Ax= X - X; Kinematics Equations (constant acceleration) Ax V = V.; + a At average velocity At 1 Xf = X, +v .At+-a,At2 total distance 2 average speed total time (v, = (v )= + 2a, Ax dx instantaneous velocity V dt Free Fall instantaneous speed vx On Earth, when not touching anything, objects fall due to Av. V average acceleration Vi gravity towards the Earth's At center with acceleration: d' x g = 9.80 m/$2 instantaneous acceleration dv dt dt2 (neglecting air resistance)do VE W = speed dt angular speed dt 2Tr v = 2arf = T W = 2nf = angular speed T speed Angular speed does not depend on radius linear angular position Ar de velocity V = W = dt dt dw acceleration 0 = O = dt dt Galilean Transformations Position X= X-VI V- y+VI V-y-VI E - E+VI E=E-VI S velocity measured in s' Velocity velocity measured in s u = u- V u = utv velocity of s' relative to sExam 2 Topics The topics covered in the second exam are from the first eight chapters of the book. While the focus will be on Chapter 4, Chapter 5, Chapter 6, Chapter 7, and Chapter 8, material from earlier chapters is highly used in these four chapters. Topics you might find are: . Newton's First Law . Newton's Second Law (F=ma) . Tension Interactions . Newton's Third Law . Frictional Forces (Static versus Kinetic) . Circular Motion . Uniform and Nonuniform . Altered Coordinate System . Angular Kinematics . Interactions with Cartesian (Linear) Kinematics . Centrifugal Force . Energy (Kinetic, Gravitational Potential, Elastic Potential) . Work (for constant and variable forces) . Work-Energy Theorem Power . Internal Energy Changes . Conservative vs Nonconservative Forces . Momentum . Conservation of Momentum . Elastic versus Inelastic Collisions . Kinetic Energy Considerations of Collisions . Center of Mass7. (10 Points) In the figure below, three masses are attached across two ropes. Mass 1 is 1kg, Mass 2 is 5 kg, and Mass 3 is 2 kg. Mass 2 is connected to Mass 1 through one rope over two pulleys, and connected to Mass 3 from another rope over two pulleys. Mass two is sitting on a trap door. Assume frictionless and massless pulleys and strings. 1 a) Begin with the case where Mass 2 is sitting on the trap door while it is closed, as if it was a normal table. What is the normal force between the table and Mass 2 equal to? b) Now assume the trap door opens, and Mass 2 starts falling downwards. This causes Mass 1 and Mass 3 to start moving upwards. What is the acceleration that Mass 1 moves upwards with? What about Mass 3?2. (2 Points) In a force vs displacement graph, you can find the work a force acts over a distance by finding the "area under the curve". Walk me through how you can find the work done by the object back on the thing providing the force. 3. (2 Points) What does it mean, in terms of physics and the variables associated with physics, for an item to be in equilibrium? What are the types of equilibrium, and how do they differ? 4. (2 Points) Why is it that an object that adds energy by providing work, or giving heat, or giving some other variation of energy, does not break the Law of Conservation of Energy? 5. (2 Points) A hose sprays out 10 kg of water horizontally at 20 m/s. If it does this over two minutes, what is the average power output of the hose?Work Out: For the following questions, show all calculations for full credit. 6. (10 Points) Take an alternate form of Hooke's Law that has additional terms dependent on spring displacement. The one-dimensional equation is modeled by Fx = Ax' + Bx + C, A = 30- B = 40- where m m, and C = -5NV. What is the total work done on the spring to compress the spring from equilibrium by 50 cm? What is the work done by the spring to return to equilibrium