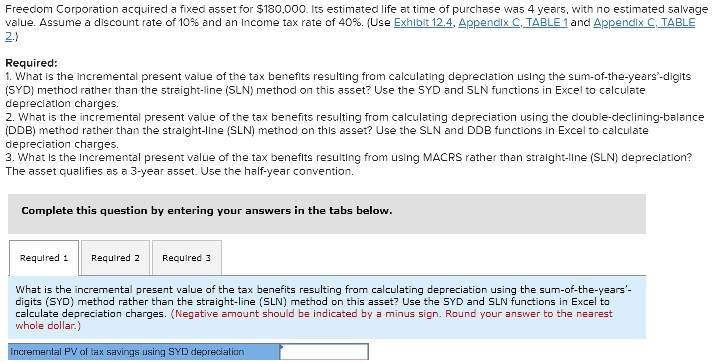
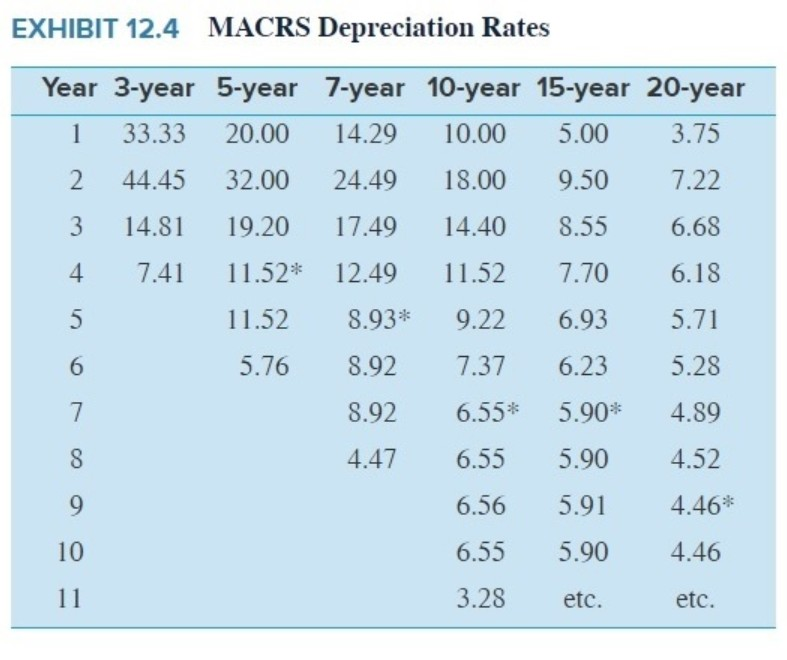
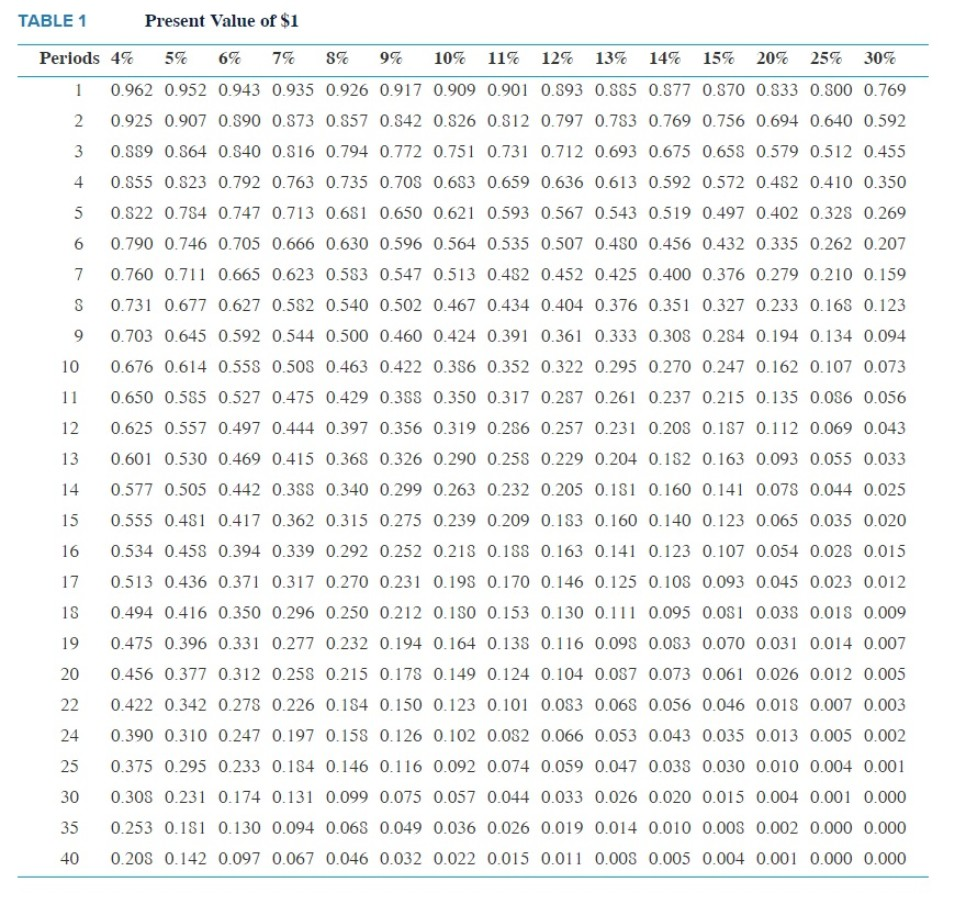
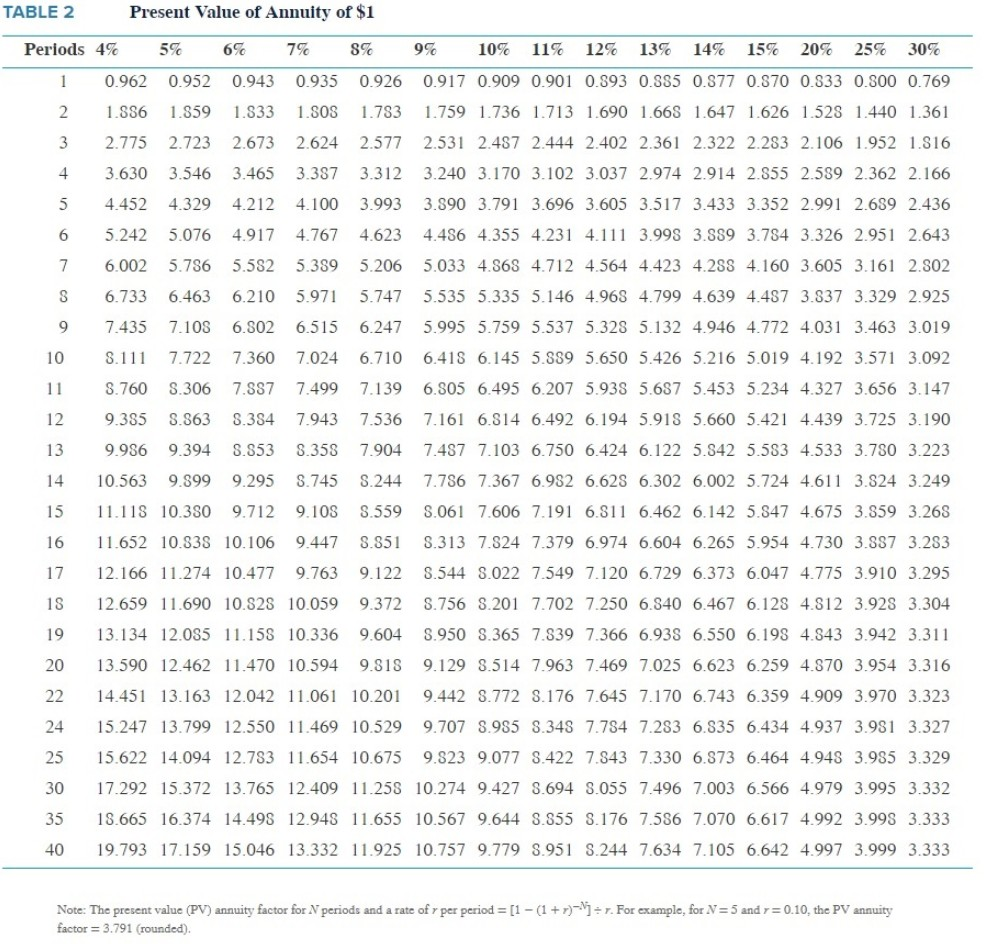
Freedom Corporation acquired a fixed asset for $180.000. Its estimated life at time of purchase was 4 years, with no estimated salvage value. Assume a discount rate of 10% and an income tax rate of 40%. (Use Exhibit 12.4, Appendix C. TABLE 1 and Appendix C. TABLE Required: 1. What is the incremental present value of the tax benefits resulting from calculating depreciation Lising the sum-of-the-years-digits (SYD) method rather than the straight-line (SLN) method on this asset? Use the SYD and SLN functions in Excel to calculate depreciation charges. 2. What is the incremental present value of the tax benefits resulting from calculating depreciation using the double-declining-balance (DDB) method rather than the straight-line (SLN) method on this asset? Use the SLN and DDB functions in Excel to calculate depreciation charges. 3. What is the incremental present value of the tax benefits resulting from using MACRS rather than straight-line (SLN) depreciation? The asset qualifies as a 3-year asset. Use the half-year convention Complete this question by entering your answers in the tabs below. Required 1 Required 2 Required 3 What is the incremental present value of the tax benefits resulting from calculating depreciation using the sum-of-the-years' digits (SYD) method rather than the straight-line (SLN) method on this asset? Use the SYD and SLN functions in Excel to calculate depreciation charges. (Negative amount should be indicated by a minus sign. Round your answer to the nearest whole dollar.) Incremental PV of tax savings using SYD depreciation What is the incremental present value of the tax benefits resulting from calculating depreciation using the double-declining- balance (DDB) method rather than the straight-line (SLN) method on this asset? Use the SLN and DDB functions in Excel to calculate depreciation charges. (Negative amount should be indicated by a minus sign. Round your answer to the nearest whole dollar.) Show less Incremental PV of tax savings using DDB depreciation What is the incremental present value of the tax benefits resulting from using MACRS rather than straight-line (SLN) depreciation? The asset qualifies as a 3-year asset. Use the half-year convention. (Negative amount should be indicated by a minus sign. Round your answer to the nearest whole dollar.) Incremental PV of tax savings using MACRS depreciation EXHIBIT 12.4 MACRS Depreciation Rates Year 3-year 5-year 7-year 10-year 15-year 20-year 1 33.33 20.00 14.29 10.00 5.00 3.75 2 44.45 32.00 24.49 18.00 9.50 7.22 3 14.81 19.20 17.49 14.40 8.55 6.68 4 7.41 11.52* 12.49 11.52 7.70 6.18 11.52 8.93* 9.22 6.93 5.71 5.76 8.92 7.37 6.23 5.28 8.92 6.55* 5.90* 4.89 4.47 6.55 5.90 4.52 6.56 5.91 4.46* 6.55 5.90 4.46 3.28 etc. etc. TABLE 1 Present Value of $1 12 0.623 Periods 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15% 20% 25% 30% 1 0.962 0.952 0.943 0.935 0.926 0.917 0.909 0.901 0.393 0.885 0.877 0.870 0.833 0.500 0.769 2 0.925 0.907 0.590 0.373 0.357 0.542 0.826 0.812 0.797 0.783 0.769 0.756 0.694 0.640 0.592 3 0.389 0.864 0.340 0.816 0.794 0.772 0.751 0.731 0.712 0.693 0.675 0.658 0.579 0.512 0.455 4 0.855 0.823 0.792 0.763 0.735 0.708 0.683 0.659 0.636 0.613 0.592 0.572 0.482 0.410 0.350 5 0.322 0.784 0.747 0.713 0.681 0.650 0.621 0.593 0.567 0.543 0.519 0.497 0.402 0.328 0.269 6 0.790 0.746 0.705 0.666 0.630 0.596 0.564 0.535 0.507 0.450 0.456 0.432 0.335 0.262 0.207 7 0.760 0.711 0.665 0.623 0.583 0.547 0.513 0.482 0.452 0.425 0.400 0.376 0.279 0.210 0.159 s 0.731 0.677 0.627 0.582 0.540 0.502 0.467 0.434 0.404 0.376 0.351 0.327 0.233 0.168 0.123 9 0.703 0.645 0.592 0.544 0.500 0.460 0.424 0.391 0.361 0.333 0.308 0.284 0.194 0.134 0.094 10 0.676 0.614 0.558 0.505 0.463 0.422 0.386 0.352 0.322 0.295 0.270 0.247 0.162 0.107 0.073 11 0.650 0.585 0.527 0.475 0.429 0.388 0.350 0.317 0.287 0.261 0.237 0.215 0.135 0.036 0.056 0.625 0.557 0.497 0.444 0.397 0.356 0.319 0.286 0.257 0.231 0.208 0.187 0.112 0.069 0.043 13 0.601 0.530 0.469 0.415 0.368 0.326 0.290 0.25% 0.229 0.204 0.182 0.163 0.093 0.055 0.033 14 0.577 0.505 0.442 0.388 0.340 0.299 0.263 0.232 0.205 0.151 0.160 0.141 0.078 0.044 0.025 15 0.555 0.481 0.417 0.362 0.315 0.275 0.239 0.209 0.183 0.160 0.140 0.123 0.065 0.035 0.020 16 0.534 0.458 0.394 0.339 0.292 0.252 0.218 0.18 0.163 0.141 0.123 0.107 0.054 0.028 0.015 0.513 0.436 0.371 0.317 0.270 0.231 0.198 0.170 0.146 0.125 0.108 0.093 0.045 0.023 0.012 18 0.494 0.416 0.350 0.296 0.250 0.212 0.180 0.153 0.130 0.111 0.095 0.081 0.035 0.018 0.009 190.475 0.396 0.331 0.277 0.232 0.194 0.164 0.138 0.116 0.098 0.083 0.070 0.031 0.014 0.007 20 0.456 0.377 0.312 0.25% 0.215 0.178 0.149 0.124 0.104 0.087 0.073 0.061 0.026 0.012 0.005 22 0.422 0.342 0.278 0.226 0.154 0.150 0.123 0.101 0.083 0.068 0.056 0.046 0.018 0.007 0.003 0.390 0.310 0.247 0.197 0.158 0.126 0.102 0.032 0.066 0.053 0.043 0.035 0.013 0.005 0.002 25 0.375 0.295 0.233 0.134 0.146 0.116 0.092 0.074 0.059 0.047 0.038 0.030 0.010 0.004 0.001 30 0.308 0.231 0.174 0.131 0.099 0.075 0.057 0.044 0.033 0.026 0.020 0.015 0.004 0.001 0.000 35 0.253 0.181 0.130 0.094 0.068 0.049 0.036 0.026 0.019 0.014 0.010 0.008 0.002 0.000 0.000 40 0.208 0.142 0.097 0.067 0.046 0.032 0.022 0.015 0.011 0.008 0.005 0.004 0.001 0.000 0.000 TABLE2 Present Value of Annuity of $1 Periods 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15% 20% 25% 30% 0.962 0.952 0.943 0.935 0.926 0.917 0.909 0.901 0.893 0.885 0.877 0.870 0.833 0.800 0.769 1.836 1.559 1.533 1.SOS 1.783 1.759 1.736 1.713 1.690 1.66S 1.647 1.626 1.528 1.440 1.361 3 2.775 2.723 2.673 2.624 2.577 2.531 2.487 2.444 2.402 2.361 2.322 2.283 2.106 1.952 1.816 3.630 3.546 3.465 3.387 3.312 3.240 3.170 3.102 3.037 2.974 2.914 2.855 2.539 2.362 2.166 4.452 4.329 4.212 4.100 3.993 3.390 3.791 3.696 3.605 3.517 3.433 3.352 2.991 2.689 2.436 6 5.242 5.076 4.917 4.767 4.623 4.486 4.355 4.231 4.111 3.995 3.889 3.784 3.326 2.951 2.643 7 6.0025.786 5.582 5.389 5.20 5.033 4.863 4.712 4.564 4.423 4.288 4.160 3.605 3.161 2.502 8 6.733 6.463 6.210 5.971 5.747 5.535 5.335 5.146 4.96S 4.799 4.639 4.487 3.837 3.329 2.925 9 7.435 7.108 6.802 6.515 6.247 5.995 5.759 5.537 5.328 5.132 4.946 4.772 4.031 3.463 3.019 8.111 7.722 7.360 7.024 6.710 6.418 6.145 5.889 5.650 5.426 5.216 5.019 4.192 3.571 3.092 3.760 3.306 7.387 7.499 7.139 6.505 6.495 6.207 5.939 5.687 5.453 5.234 4.327 3.656 3.147 12 9.385 5.563 3.384 7.943 7.536 7.161 6.814 6.492 6.194 5.918 5.660 5.421 4.439 3.725 3.190 9.986 9.394 8.553 3.358 7904 7.487 7.103 6.750 6.424 6.122 5.342 5.583 4.533 3.750 3.223 10.563 9.999 9.295 3.745 8.244 7.786 7.367 6.982 6.628 6.302 6.002 5.724 4.611 3.824 3.249 15 11.118 10.380 9.712 9.108 3.559 8.061 7.606 7.191 6.511 6.462 6.142 5.547 4.675 3.359 3.268 16 11.652 10.838 10.106 9.447 3.351 3.313 7.824 7.379 6.974 6.604 6.265 5.954 4.730 3.887 3.283 17 12.166 11.274 10.477 9.763 9.122 8.544 8.022 7.549 7.120 6.729 6.373 6.047 4.775 3.910 3.295 18 12.659 11.690 10.528 10.059 9.372 5.756 3.201 7.702 7.250 6.540 6.467 6.128 4.812 3.928 3.304 19 13.134 12.035 11.158 10.336 9.604 8.950 3.365 7.839 7.366 6.938 6.550 6.193 4.343 3.942 3.311 20 13.590 12.462 11.470 10.594 9.818 9.129 3.514 7.963 7.469 7.025 6.623 6.259 4.570 3.954 3.316 14.451 13.163 12.042 11.061 10.201 9.442 3.772 8.176 7.645 7.170 6.743 6.359 4.909 3.970 3.323 24 15.247 13.799 12.550 11.469 10.529 9.707 8.985 .348 7.784 7.283 6.535 6.434 4.937 3.981 3.327 25 15.622 14.094 12.783 11.654 10.675 9.823 9.077 3.422 7.843 7.330 6.573 6.464 4.948 3.985 3.329 30 17.292 15.372 13.765 12.409 11.258 10.274 9.427 8.694 5.055 7.496 7.003 6.566 4.979 3.995 3.332 35 18.665 16.374 14.498 12.948 11.655 10.567 9.644 3.855 3.176 7.556 7.070 6.617 4.992 3.999 3.333 40 19.793 17.159 15.046 13.332 11.925 10.757 9.779 5.951 5.244 7.634 7.105 6.642 4.997 3.999 3.333 Note: The present value (PV) annuity factor for N periods and a rate of r per period = [1 - (1 + r)- = r. For example, for N=5 and r=0.10, the PV annuity factor = 3.791 (rounded)