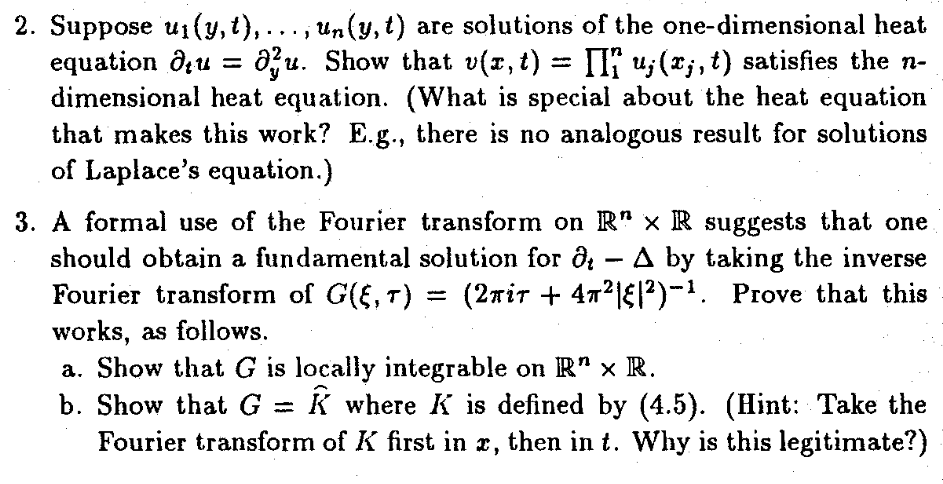
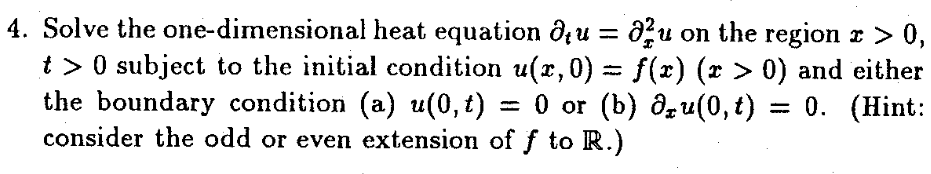
From Gerald Folland's book named as Introduction to Partial Differential Equations. Please help with these problems AS SOON AS POSSIBLE!

MANY THANKS IN ADVANCE!!!

So, we need to solve these above-listed exercises. They are from the section about the Heat operator. Please ask me what exactly I should specify, since the questions are taken from the book. They need to be solved as soon as possible.

Best regards for all of you. Hope for your help.

2. Suppose ui(y,t),..., Un(y, t) are solutions of the one-dimensional heat equation du = 0;4. Show that v(x, t) = [1 uj(Fj, t) satisfies the n- dimensional heat equation. (What is special about the heat equation that makes this work? E.g., there is no analogous result for solutions of Laplace's equation.) 3. A formal use of the Fourier transform on R" x R suggests that one should obtain a fundamental solution for de - Aby taking the inverse Fourier transform of G(E,T) (2nit + 4721812)-1. Prove that this works, as follows. a. Show that G is locally integrable on R" R. b. Show that G where K is defined by (4.5). (Hint: Take the Fourier transform of K first in z, then in t. Why is this legitimate?) 4. Solve the one-dimensional heat equation Otu : ou on the region 2 > 0, t> 0 subject to the initial condition u(x,0) = f(x) (x > 0) and either the boundary condition (a) u(0,t) = 0 or (b) 0; u(0,t) = 0. (Hint: consider the odd or even extension of f to R.) 2. Suppose ui(y,t),..., Un(y, t) are solutions of the one-dimensional heat equation du = 0;4. Show that v(x, t) = [1 uj(Fj, t) satisfies the n- dimensional heat equation. (What is special about the heat equation that makes this work? E.g., there is no analogous result for solutions of Laplace's equation.) 3. A formal use of the Fourier transform on R" x R suggests that one should obtain a fundamental solution for de - Aby taking the inverse Fourier transform of G(E,T) (2nit + 4721812)-1. Prove that this works, as follows. a. Show that G is locally integrable on R" R. b. Show that G where K is defined by (4.5). (Hint: Take the Fourier transform of K first in z, then in t. Why is this legitimate?) 4. Solve the one-dimensional heat equation Otu : ou on the region 2 > 0, t> 0 subject to the initial condition u(x,0) = f(x) (x > 0) and either the boundary condition (a) u(0,t) = 0 or (b) 0; u(0,t) = 0. (Hint: consider the odd or even extension of f to R.)