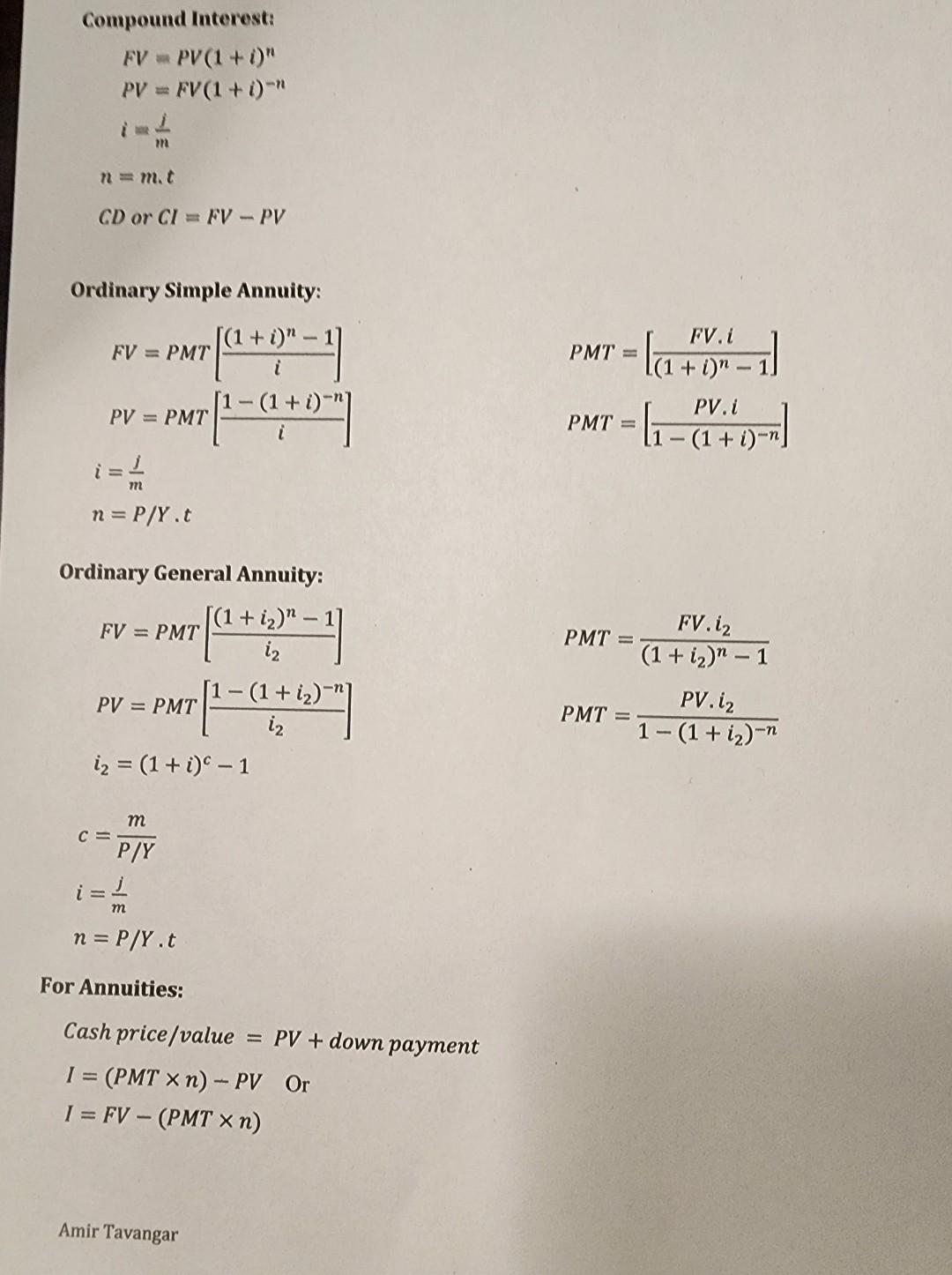
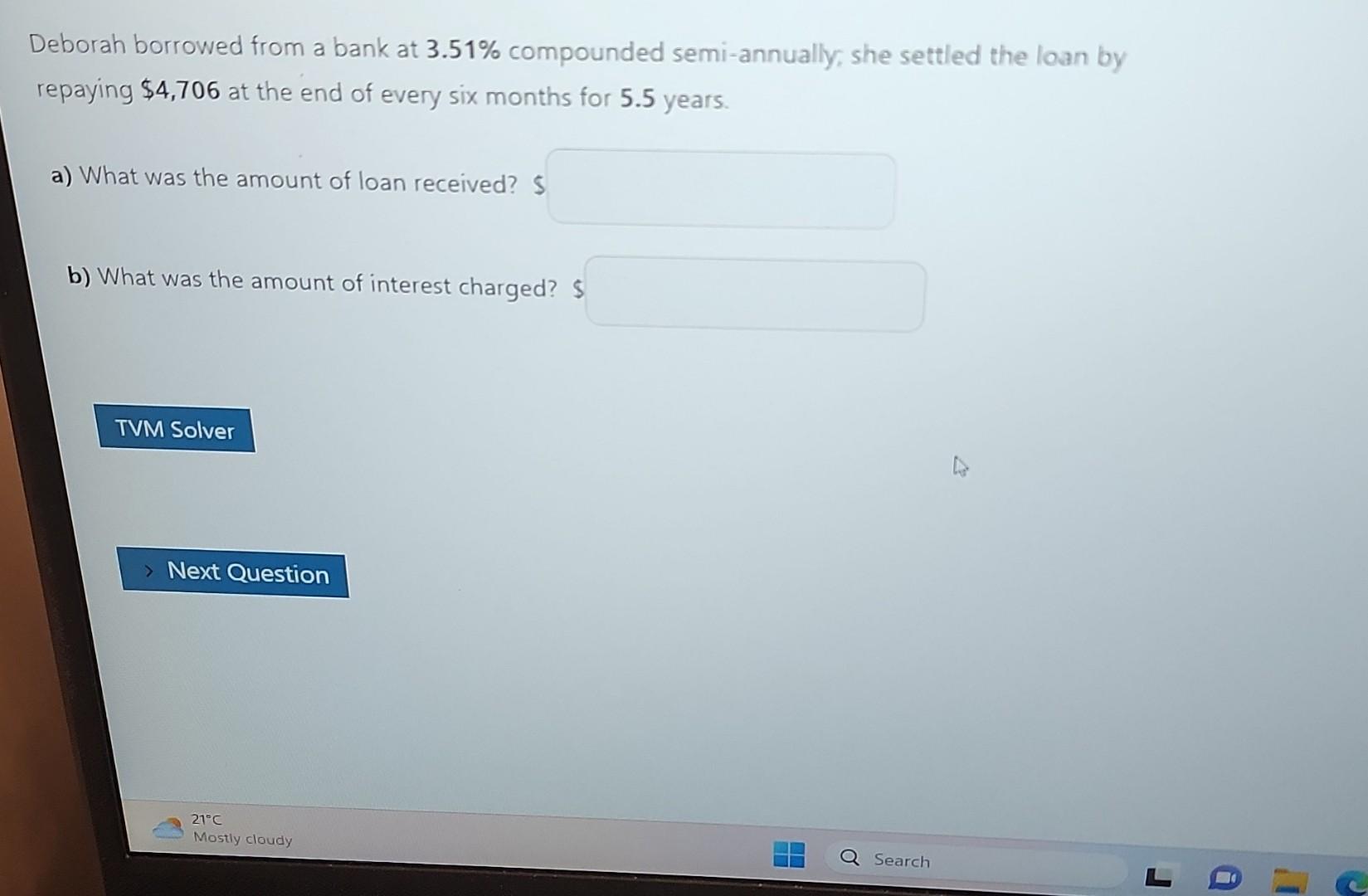
- FVg = the future value (or accumulated value) of an ordinary general annuity) - \\( P M T= \\) the size of the periodic payment - J=nominal interest rate - \\( n= \\) the number of periodic payments \\( n=p / y^{*} t \\) - \\( c= \\) the number of interest conversion periods per payment interval \\( =\\frac{m}{p / y} \\) - \\( \\quad i= \\) the interest rate per interest conversion period \\( =\\frac{j}{m} \\) - \\( p= \\) the equivalent rate of interest per payment period \\[ \\begin{array}{l} F V_{n}=P M T\\left[\\frac{(1+i)^{n}-1}{i}\ ight] \\\\ P V_{n}=P M T\\left[\\frac{1-(1+i)^{-n}}{i}\ ight] \\\\ P M T=\\left[\\frac{F V_{n} i}{(1+i)^{n}-1}\ ight] \\\\ P M T=\\left[\\frac{P V_{n} i}{1-(1+i)^{-n}}\ ight] \\\\ c=\\frac{\\text { THE NUMBER OF INTEREST CONVERSION PERIODS PER YEAR }}{T H}=\\frac{m}{p / y} \\\\ p=(1+i)^{c}-1 \\\\ F V_{g}=P M T\\left[\\frac{(1+p)^{n}-1}{p}\ ight] \\\\ P V_{g}=P M T\\left[\\frac{1-(1+p)^{-n}}{p}\ ight] \\\\ P M T=\\frac{F V_{g} p}{(1+p)^{n}-1} \\\\ P M T=\\frac{P V_{g} p}{1-(1+p)^{-n}} \\end{array} \\] Compound interest \\[ \\begin{array}{l} F V=P V(1+i)^{n} \\\\ P V=\\frac{F V}{(1+i)^{n}} \\text { or. } P V=F V(1+i)^{-n} \\end{array} \\] Compound Interest: \\[ \\begin{array}{l} F V=P V(1+i)^{n} \\\\ P V=F V(1+i)^{-n} \\\\ i=\\frac{1}{m} \\\\ n=m \\cdot t \\\\ C D \\text { or } C I=F V-P V \\end{array} \\] Ordinary Simple Annuity: \\[ \\begin{array}{l} F V=P M T\\left[\\frac{(1+i)^{n}-1}{i}\ ight] \\\\ P V=P M T\\left[\\frac{1-(1+i)^{-n}}{i}\ ight] \\\\ i=\\frac{j}{m} \\\\ n=P / Y . t \\end{array} \\] \\[ \\begin{array}{l} P M T=\\left[\\frac{F V \\cdot i}{(1+i)^{n}-1}\ ight] \\\\ P M T=\\left[\\frac{P V \\cdot i}{1-(1+i)^{-n}}\ ight] \\end{array} \\] Ordinary General Annuity: \\[ \\begin{array}{l} F V=P M T\\left[\\frac{\\left(1+i_{2}\ ight)^{n}-1}{i_{2}}\ ight] \\\\ P V=P M T\\left[\\frac{1-\\left(1+i_{2}\ ight)^{-n}}{i_{2}}\ ight] \\\\ i_{2}=(1+i)^{c}-1 \\\\ c=\\frac{m}{P / Y} \\\\ i=\\frac{j}{m} \\\\ n=P / Y . t \\end{array} \\] \\[ \\begin{aligned} P M T & =\\frac{F V \\cdot i_{2}}{\\left(1+i_{2}\ ight)^{n}-1} \\\\ P M T & =\\frac{P V \\cdot i_{2}}{1-\\left(1+i_{2}\ ight)^{-n}} \\end{aligned} \\] For Annuities: Cash price \\( / \\) value \\( =P V+ \\) down payment \\[ \\begin{array}{l} I=(P M T \\times n)-P V \\quad \\text { Or } \\\\ I=F V-(P M T \\times n) \\end{array} \\] Amir Tavangar Deborah borrowed from a bank at \3.51 compounded semi-annually, she settled the loan by repaying \\( \\$ 4,706 \\) at the end of every six months for 5.5 years. a) What was the amount of loan received? 5 b) What was the amount of interest charged? \\( \\$ \\)