GAME STRATEGY

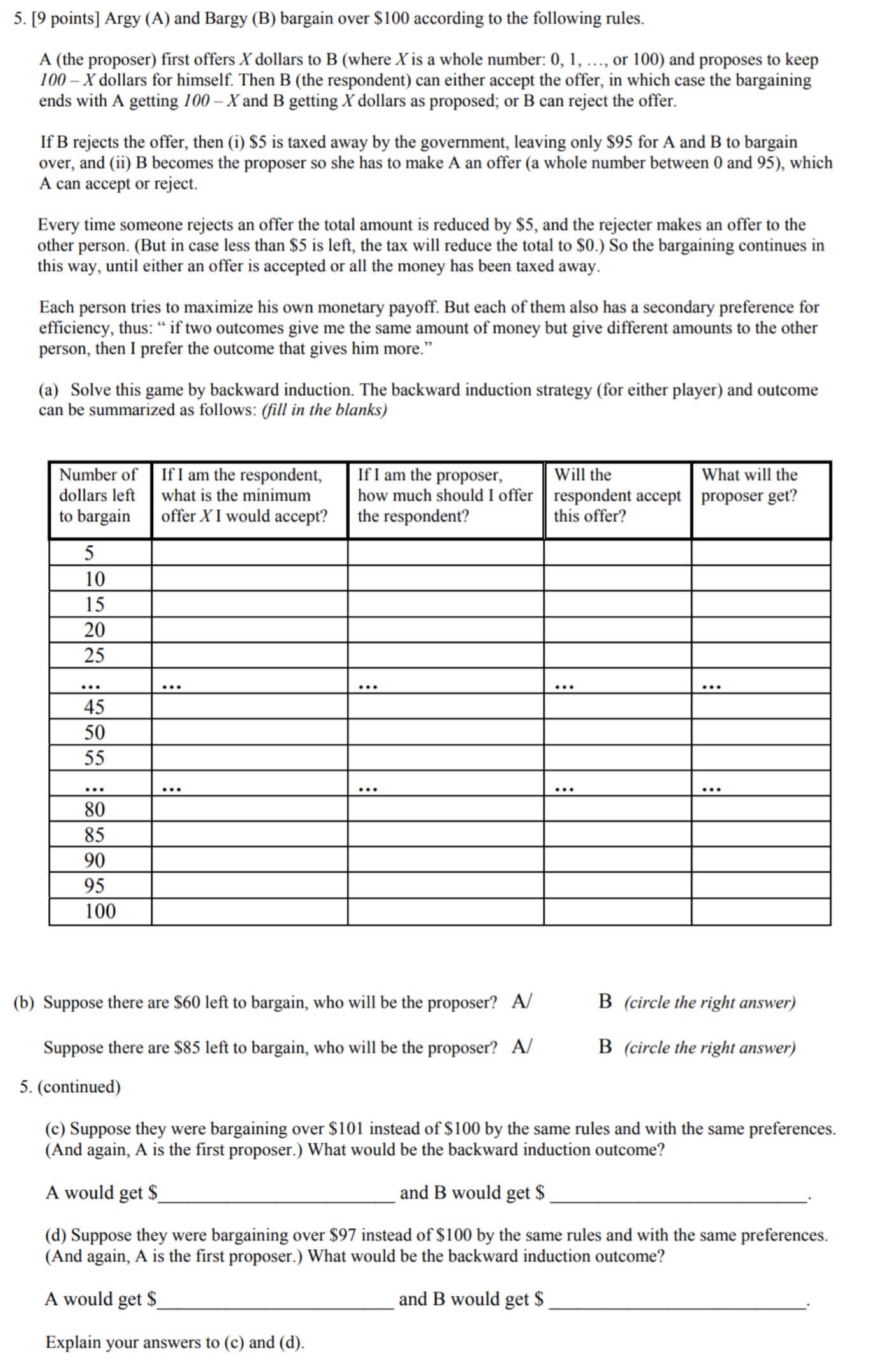
5. [9 points] Argy (A) and Bargy (B) bargain over $100 according to the following rules. A (the proposer) first offers X dollars to B (where X is a whole number: 0, 1, ..., or 100) and proposes to keep 100 - X dollars for himself. Then B (the respondent) can either accept the offer, in which case the bargaining ends with A getting 100 - X and B getting X dollars as proposed; or B can reject the offer. If B rejects the offer, then (i) $5 is taxed away by the government, leaving only $95 for A and B to bargain over, and (ii) B becomes the proposer so she has to make A an offer (a whole number between 0 and 95), which A can accept or reject. Every time someone rejects an offer the total amount is reduced by $5, and the rejecter makes an offer to the other person. (But in case less than $5 is left, the tax will reduce the total to $0.) So the bargaining continues in this way, until either an offer is accepted or all the money has been taxed away. Each person tries to maximize his own monetary payoff. But each of them also has a secondary preference for efficiency, thus: " if two outcomes give me the same amount of money but give different amounts to the other person, then I prefer the outcome that gives him more." (a) Solve this game by backward induction. The backward induction strategy (for either player) and outcome can be summarized as follows: (fill in the blanks) Number of If I am the respondent, If I am the proposer, Will the What will the dollars left what is the minimum how much should I offer respondent accept proposer get? to bargain offer X I would accept? the respondent? this offer? 5 10 15 20 25 . . . ... ... ... ... 45 50 55 . . . . . . ... . . . . . . 80 85 90 95 100 (b) Suppose there are $60 left to bargain, who will be the proposer? A/ B (circle the right answer) Suppose there are $85 left to bargain, who will be the proposer? A/ B (circle the right answer) 5. (continued) (c) Suppose they were bargaining over $101 instead of $100 by the same rules and with the same preferences. (And again, A is the first proposer.) What would be the backward induction outcome? A would get $ and B would get $ (d) Suppose they were bargaining over $97 instead of $100 by the same rules and with the same preferences. (And again, A is the first proposer.) What would be the backward induction outcome? A would get $ and B would get $ Explain your answers to (c) and (d)