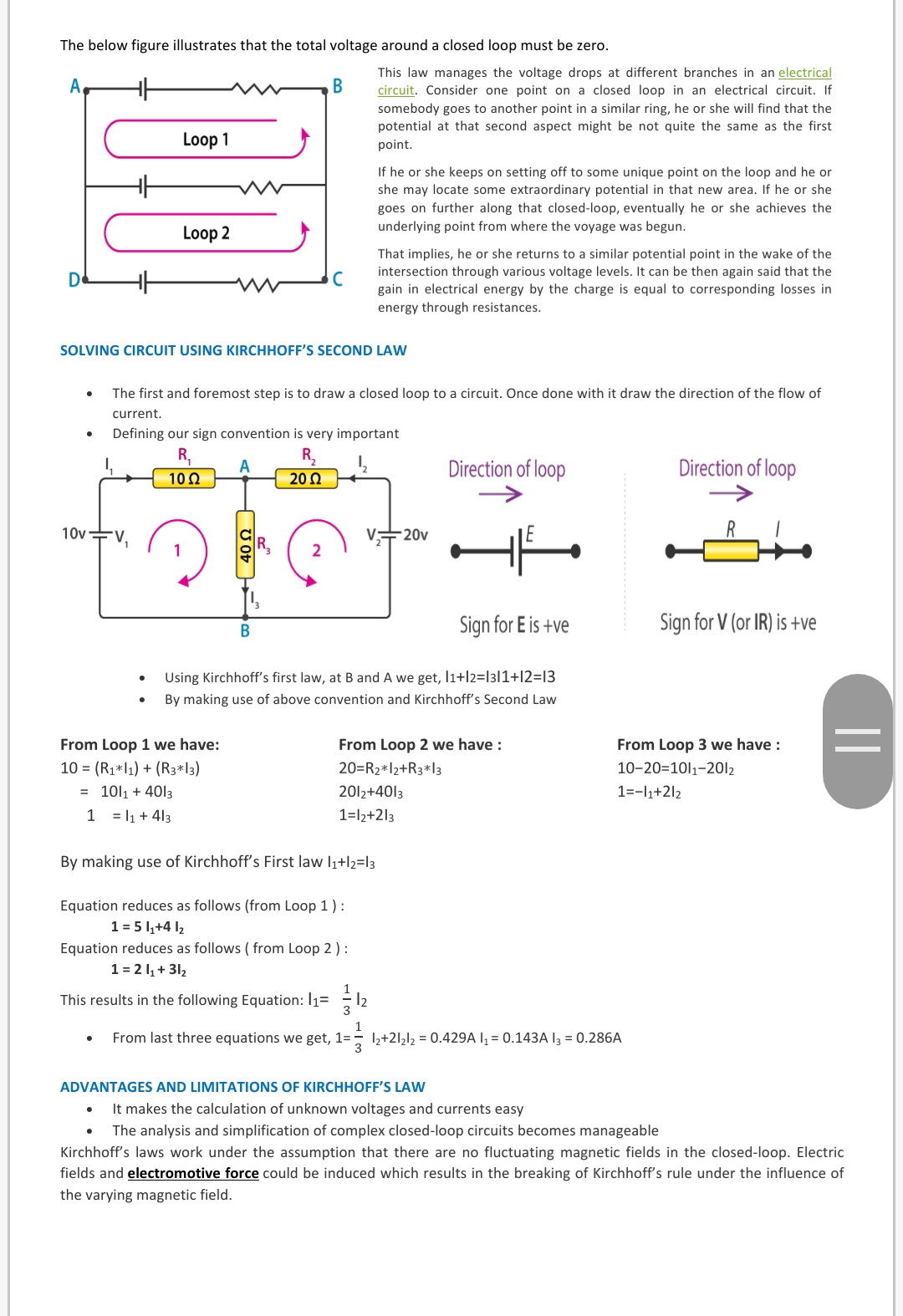
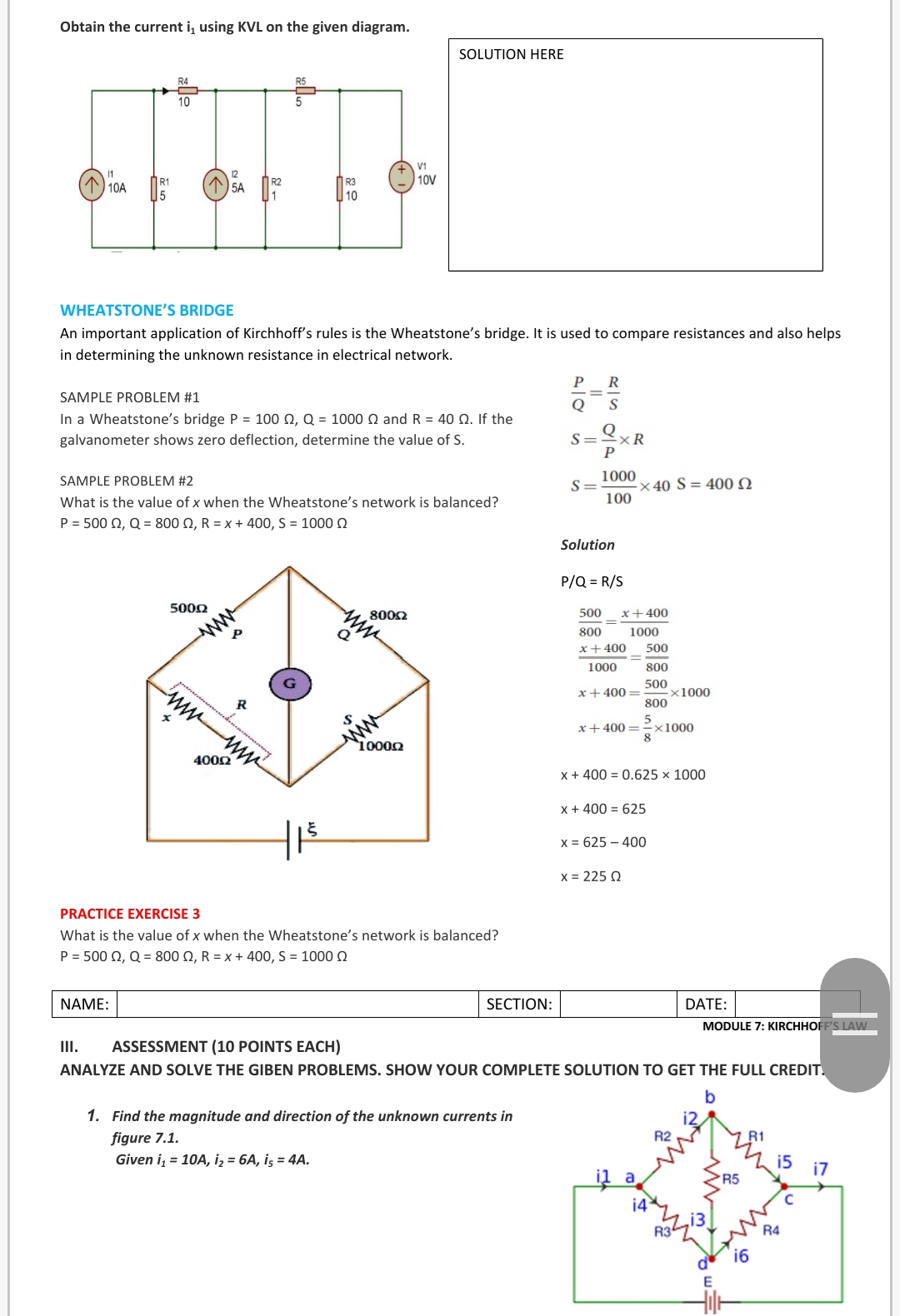
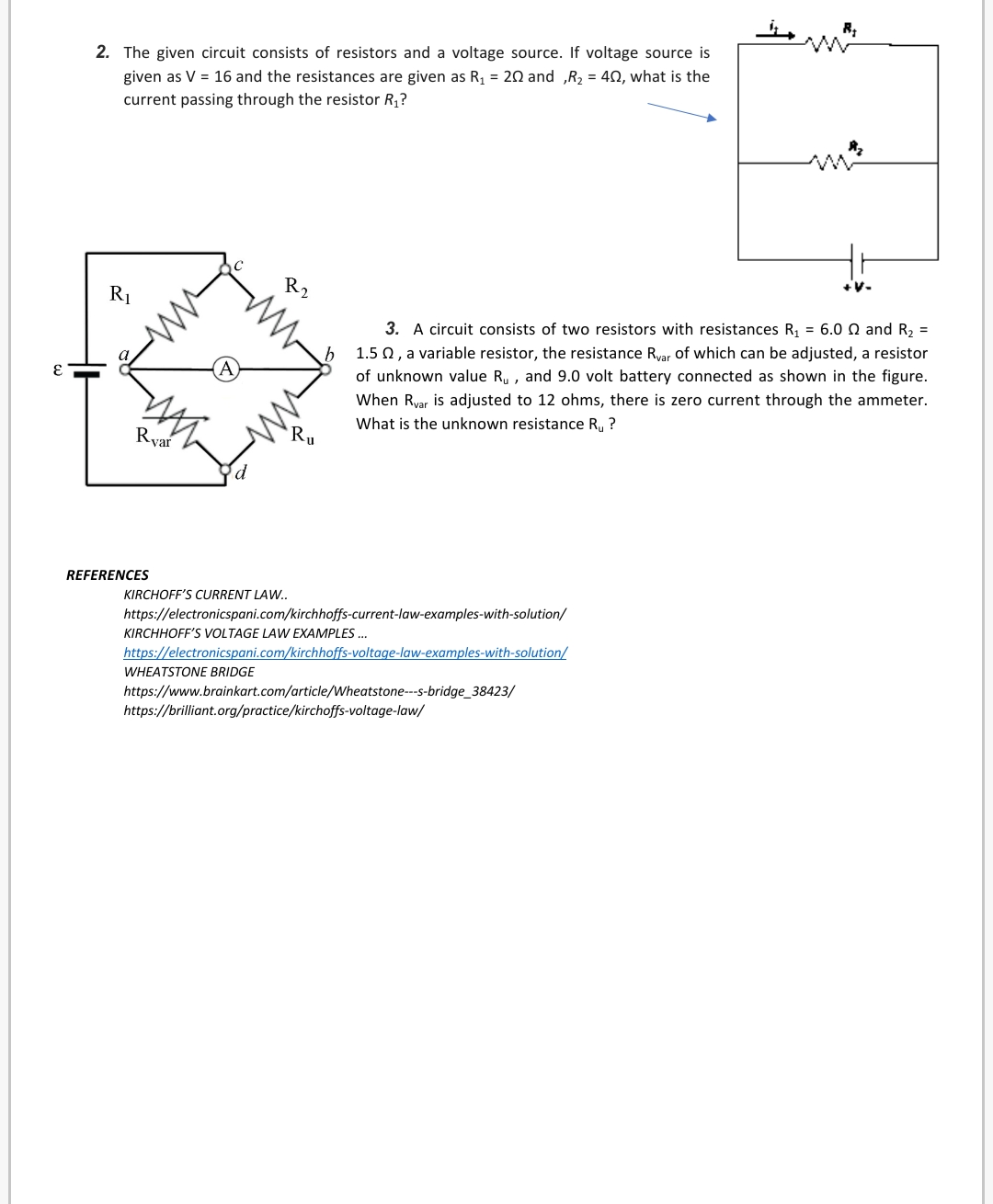
GENERAL PHYSICS 2 I. PRE-TEST {1o phi) ANALYZE AND ANSWER THE GIVEN QUESTIONS. 1. Describe Kirchhoff's First law based on Figure 1. The sum of al lhe leage D'qns sound to loop Currents Entering the Node is me I) Zero Eqrals Currants Luvinglho Nod. Iiflz+13+(-14+-I5)=D Vno+Vac+Vcn+Vmio Figure 1 KIRCHOFF'S FIRST LAW Figure 2 KIRCHOFF'S 2\"\" LAW Wrw- mMWW 2. Referring to Figure 2, describe Ki rchhoff's 2"'1 law. ll. DISCUSSION: In 1845, a German physicist, Gustav Kirchhoff developed a pair of laws that deal with the conservation of current and energy within electrical circuits. These two laws are commonly known as Kirchhoff's Voltage and Current Law. These laws help in calculating the electrical resistance ofa complex network or impedance in case of AC and the current flow in different streams of the network. In the next section, let us look at what these laws state. Kirchhoff's laws are fundamental to circuit theory. They quantify how current flows through a circuit and how voltage varies around a loop in a circuit. Kirchoff's circuit law were first described in 1845 by the German physicist Gustav Kirchhoff. What are Kirchhoff's Laws? There are two laws as follows: - Kirchhoff's first law, also known as Kirchhoff's current lavvr (KCL) states that the current owing into a node must be equal to the current flowing out of the node. This is a consequence ofcharge conservation. - Kirchhoff's second law, also known as the Kirchhofl's voltage law [IWLI states that the sum of all voltages around a closed loop in any circuit must be equal to zero. This again is a consequence of charge conservation and also conservation of energy. Kirchhoff's Junction Rule Kirchhoff's rst law goes by several names as Kirchho's Current Law {KCL}, Klrchhous Junction Rule, Klrchhof's point rule, Kirchhos nodal rule. It is an application of the principle of conservation of electric charge. The law states that at any circuit junction, the sum of the currents flowing into and out of that junction are equal. In simple terms, what KCL really says is that, The sum of all currents entering a node is equal to the sum of all currents leaving the node. We perform analysis on all nodes based on the inflow and outflow of current. Current directions at the node are based on presumed directions of the currents. As long as the assumed directions of the currents are consistent from node to node, the final result of the analysis will reflect the actual current directions in the circuit. Mathematically, Kirchhoff's Current law is stated as follows 2: 11k = 0 where n is the total number of branches carrying current towards or away from the node. Solving Circuits Using KCL Let us look at a few examples that demonstrate the law in practice and understand its importance in determining the unknown parameters. Example 1: Let us consider a network of assumed directions of the current as shown below. Let us choose a sign convention such that currents entering the node are positive, and the currents leaving the node are negative. With this convention, KCL applied at the node yields the equation: i1{t] + i2{t] ism = illt) + i2(t) - Bit) = 0 all] or, am + i2{t]=i3[t)i1[t) + 12m =i3lt) -\\ j _ _ _ lollI This amounts to the statement that the total current entering the node is the same as the total current leaving the node. Example 2: Using KCL to determine the value of the unknown current i in the circuit below. Assuming that the current entering the node is positive, the sum of the currents is given by the equation, 4A -(1A)-2A | = 04A {-1A] 2A | = 0 => 4A+1A2A = 3A =9 4A+1A2A = 3A Therefore, 3: 3A, leaving the node{since our assumed direction ofi on the diagram is that it is leaving the node, and our numerical value for i is positive]. DISADVANTAG ES OF KCL - KCL is valid only if the total electric charge is constant in the circuit. - KCL is suitable for high-frequency AC circuits. Together KIRCHOFF'S VOLTAGE LAW and the Current Law are a great pair of tools useful in analyzing electric circuits. Practice Exercise 1 Calculate the currents Land 1:, In the circuit below. f SOLUTION HERE: f mi I\" KIRCHHOFF'S VOLTAGE LAW Kirchhoff's Second Law or the voltage law states that the net electromotive force around a closed circuit loop is equal to the sum of potential drops around the loop It is termed as Kirchhoff's Loop Rule, which is an outcome of an electrostatic field that is conservative. Hence, a If a charge moves around a closed loop in a circuit, it must gain as much energy as it loses. a The above can be summarized as the gain in energy by the charge = corresponding losses in energy through resistances - Mathematically, the total voltage in a closed loop of a circuit is expressed as {V = CI The below figure illustrates that the total voltage around a closed loop must be zero. This law manages the voltage drops at different branches in an electrical B circuit. Consider one point on a closed loop in an electrical circuit. If somebody goes to another point in a similar ring, he or she will find that the potential at that second aspect might be not quite the same as the first Loop 1 point. If he or she keeps on setting off to some unique point on the loop and he or she may locate some extraordinary potential in that new area. If he or she goes on further along that closed-loop, eventually he or she achieves the Loop 2 underlying point from where the voyage was begun. That implies, he or she returns to a similar potential point in the wake of the intersection through various voltage levels. It can be then again said that the gain in electrical energy by the charge is equal to corresponding losses in energy through resistances. SOLVING CIRCUIT USING KIRCHHOFF'S SECOND LAW The first and foremost step is to draw a closed loop to a circuit. Once done with it draw the direction of the flow of current. Defining our sign convention is very important R, 10 0 20 0 Direction of loop Direction of loop 10V V, + 20v 40 0 R 3 Sign for E is +ve Sign for V (or IR) is +ve Using Kirchhoff's first law, at B and A we get, l1+12=1311+12=13 By making use of above convention and Kirchhoff's Second Law From Loop 1 we have: From Loop 2 we have : From Loop 3 we have : 10 = (R1*/1) + (R3*13) 20=R2*12+R3*13 10-20=10|1-2012 = 10|1 + 4013 2012+4013 1=-11+212 1 = |1 + 413 1=12+213 By making use of Kirchhoff's First law |1+12=13 Equation reduces as follows (from Loop 1 ) : 1 =51,+4 12 Equation reduces as follows ( from Loop 2 ) : 1 = 211+ 312 This results in the following Equation: |1= = 12 From last three equations we get, 1= 2 12+212/2 = 0.429A l, = 0.143A 13 = 0.286A ADVANTAGES AND LIMITATIONS OF KIRCHHOFF'S LAW It makes the calculation of unknown voltages and currents easy The analysis and simplification of complex closed-loop circuits becomes manageable Kirchhoff's laws work under the assumption that there are no fluctuating magnetic fields in the closed-loop. Electric fields and electromotive force could be induced which results in the breaking of Kirchhoff's rule under the influence of the varying magnetic field.Obtain the current i1 using KVL on the given diagram. SOLUTION HERE VI 10! "IA _. WHEATSTONE'S BRIDGE An important application of Kirchhoff's rules is the Wheatstone's bridge. It is used to compare resistances and also helps in determining the unknown resistance in electrical network. P _ R SAMPLE PROBLEM #1 6 E In a Wheatstone's bridge P = 100 Q, Q = 1000 0 and R = 40 0. If the Q galvanometer shows zero deflection, determine the value of S. S = 3 x R SAMPLE PROBLEM #2 5: 1000x40 3:400!) What is the value ofx when the Wheatstone's network is balanced? 100 P = 500 0,0: 8000, R=x+400,S= 10000 Solution Pia: Ms E x+400 300 1000 x + 400 _ 500 1000 _ 300 x + 400 = Ex 1000 800 5 x+400=x1000 x + 400 = 0.525 x 1000 x + 400 = 625 x = 625 400 x = 225 0 PRACTICE EXERCISE 3 What is the value ofx when the Wheatstone's network is balanced? P = 500 0,0: 8000, R=x+400,S= 10000 NAME: SECTION: DATE: MODULE 7: KIRCHHO III. ASSESSMENT [10 POINTS EACH) ANALYZE AND SOLVE THE GIBEN PROBLEMS. SHOW YOUR COMPLETE SOLUTION TO GET THE FULL CREDI 1. Find the magnitude and direction of the unknown currents in figure 7.1. Give" it = I\2. The given circuit consists of resistors and a voltage source. If voltage source is given as V = 16 and the resistances are given as R1 = 20 and , R2 = 40, what is the current passing through the resistor R,? R1 R 2 3. A circuit consists of two resistors with resistances R1 = 6.0 0 and R2 = 1.5 0, a variable resistor, the resistance Roar of which can be adjusted, a resistor 3 of unknown value Ru , and 9.0 volt battery connected as shown in the figure. When Rvar is adjusted to 12 ohms, there is zero current through the ammeter. Ru What is the unknown resistance Ru ? Ryar REFERENCES KIRCHOFF'S CURRENT LAW.. https://electronicspani.com/kirchhoffs-current-law-examples-with-solution/ KIRCHHOFF'S VOLTAGE LAW EXAMPLES .. https://electronicspani.com/kirchhoffs-voltage-law-examples-with-solution/ WHEATSTONE BRIDGE https://www.brainkart.com/article/Wheatstone---s-bridge_38423/ https://brilliant.org/practice/kirchoffs-voltage-law/