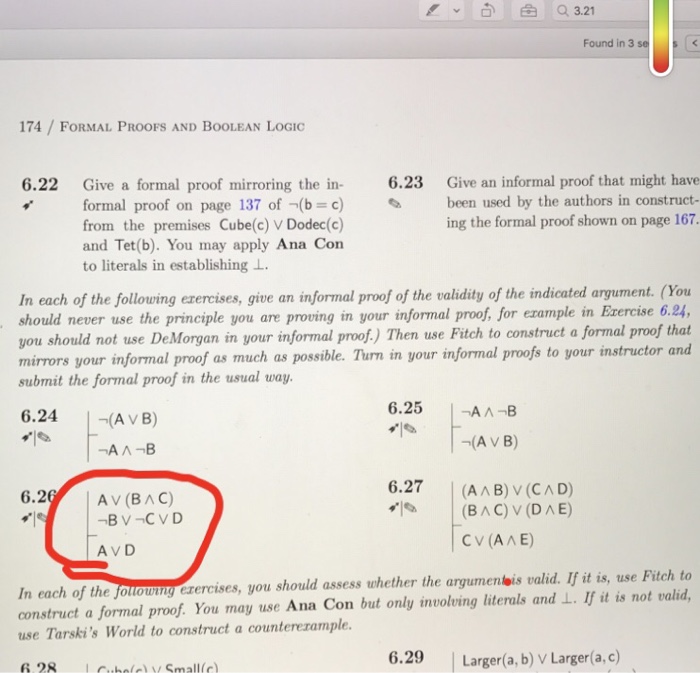
Give a formal proof mirroring the informal proof on page 137 of not (b = c) from the premises Cube(c) V Dodec (c) and Tet (b). You may apply Ana Con to literals in establishing perpendicular. Give an informal proof that might have been used by the authors in constructing the formal proof shown on page 167. In each of the following exercises, give an informal proof of the validity of the indicated argument. (You should never use the principle you are proving in your informal proof, for example in Exercise 6.24, you should not use DeMorgan in your informal proof.) Then use Fitch to construct a formal proof that mirrors your informal proof as much as possible. Turn in your informal proofs to your instructor and submit the formal proof in the usual way. Not (A V B) not A Lambda not B not A Lambda not B not (A V B) A V (B Lambda C) not B V not C V D A V D (A Lambda B) V (C Lambda D) (B Lambda C) V (D Lambda E) C V (A Lambda E) In each of the following exercises, you should assess whether the argument is valid. If it is, use Fitch to construct a formal proof. You may use Ana Con but only involving literals and perpendicular. If it is not valid, use Tarski's World to construct a counterexample. Give a formal proof mirroring the informal proof on page 137 of not (b = c) from the premises Cube(c) V Dodec (c) and Tet (b). You may apply Ana Con to literals in establishing perpendicular. Give an informal proof that might have been used by the authors in constructing the formal proof shown on page 167. In each of the following exercises, give an informal proof of the validity of the indicated argument. (You should never use the principle you are proving in your informal proof, for example in Exercise 6.24, you should not use DeMorgan in your informal proof.) Then use Fitch to construct a formal proof that mirrors your informal proof as much as possible. Turn in your informal proofs to your instructor and submit the formal proof in the usual way. Not (A V B) not A Lambda not B not A Lambda not B not (A V B) A V (B Lambda C) not B V not C V D A V D (A Lambda B) V (C Lambda D) (B Lambda C) V (D Lambda E) C V (A Lambda E) In each of the following exercises, you should assess whether the argument is valid. If it is, use Fitch to construct a formal proof. You may use Ana Con but only involving literals and perpendicular. If it is not valid, use Tarski's World to construct a counterexample