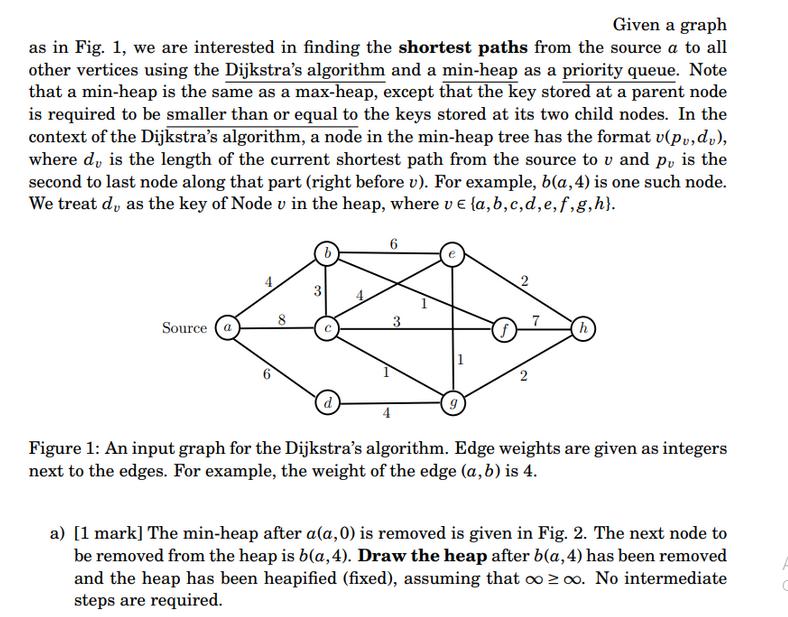
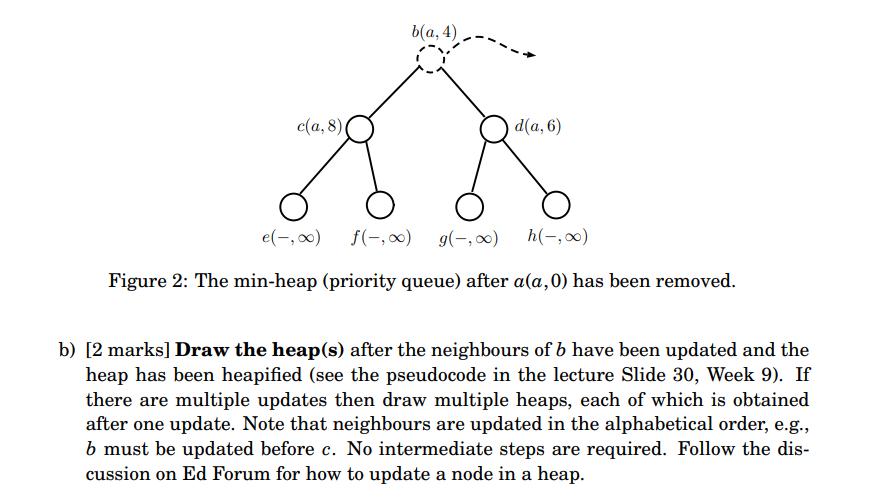
Given a graph as in Fig. 1, we are interested in finding the shortest paths from the source a to all other vertices using the Dijkstra's algorithm and a min-heap as a priority queue. Note that a min-heap is the same as a max-heap, except that the key stored at a parent node is required to be smaller than or equal to the keys stored at its two child nodes. In the context of the Dijkstra's algorithm, a node in the min-heap tree has the format v(pv, dv), where d, is the length of the current shortest path from the source to v and p, is the second to last node along that part (right before v). For example, b(a, 4) is one such node. We treat d, as the key of Node u in the heap, where uela,b,c,d,e, f,g,h}. Source: 3 C 6 h Figure 1: An input graph for the Dijkstra's algorithm. Edge weights are given as integers next to the edges. For example, the weight of the edge (a, b) is 4. a) [1 mark] The min-heap after a(a,0) is removed is given in Fig. 2. The next node to be removed from the heap is b(a, 4). Draw the heap after b(a, 4) has been removed and the heap has been heapified (fixed), assuming that co2oo. No intermediate steps are required. c(a, 8) b(a, 4) d(a, 6) e(-,0) f(-) g(,00) h(-,0) Figure 2: The min-heap (priority queue) after a(a,0) has been removed. b) [2 marks] Draw the heap(s) after the neighbours of b have been updated and the heap has been heapified (see the pseudocode in the lecture Slide 30, Week 9). If there are multiple updates then draw multiple heaps, each of which is obtained after one update. Note that neighbours are updated in the alphabetical order, e.g., 6 must be updated before c. No intermediate steps are required. Follow the dis- cussion on Ed Forum for how to update a node in a heap. 1 a(a,0) 2 a(a,0), bla,4) 3 34 4 10 5 6 S: vertices whose shortest paths have been known 7 8 c) [5 marks] Complete Table 1 with correct answers. You are required to follow strictly the steps in the Dijkstra's algorithm taught in the lecture of Week 9. d) [2 marks] Fill Table 2 with the shortest paths AND the corresponding distances from a to ALL other vertices in the format a ??v|dy, for instance, a - b 4. a a-a b a b d 2485 e f g Priority queue of remaining vertices b(a, 4), c(a, 8), d(a, 6), e(-,co), f(-,co), g(-, oo),h(-,00) Table 1: Complete this table for Part c). h Shortest Paths Table 2: Complete this table for Part d). Distances 0 4