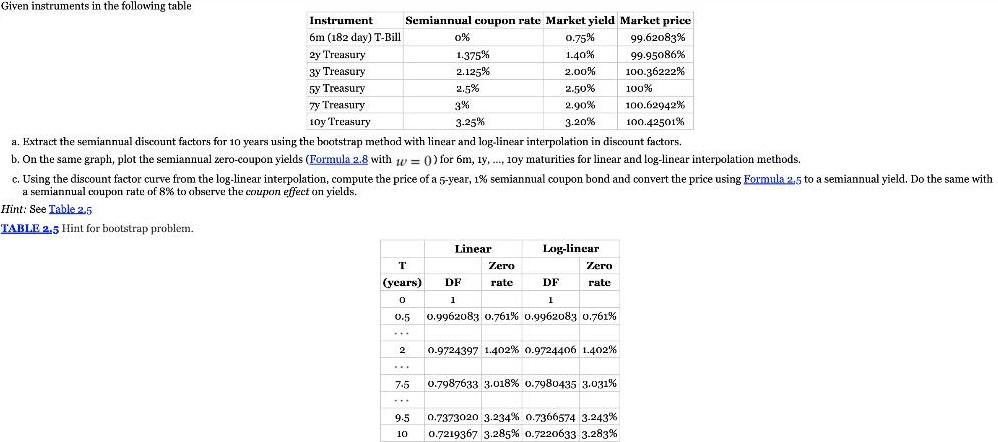
Question: Given instruments in the following table Instrument 6m (182 day) T-Bill 2y Treasury 3y Treasury 5y Treasury 7y Treasury 10y Treasury Semiannual coupon rate
![]()

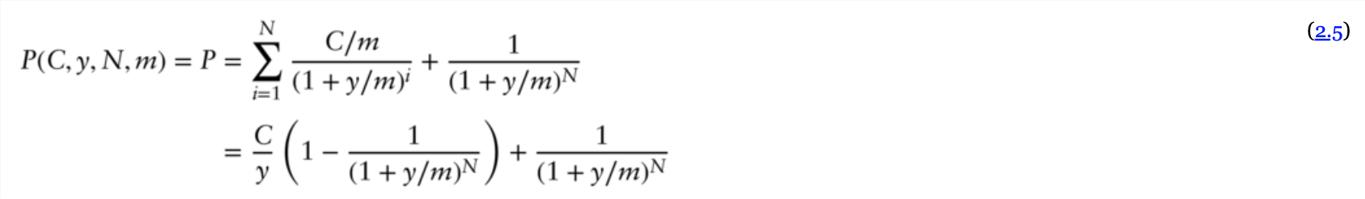
Given instruments in the following table Instrument 6m (182 day) T-Bill 2y Treasury 3y Treasury 5y Treasury 7y Treasury 10y Treasury Semiannual coupon rate Market yield Market price 0.75% 1.40% 2.00% 2.50% 2.90% 3.20% T (years) 0 a. Extract the semiannual discount factors for 10 years using the bootstrap method with linear and log-linear interpolation in discount factors. b. On the same graph, plot the semiannual zero-coupon yields (Formula 2.8 with w=0)) for 6m, 1y,.... 10y maturities for linear and log-linear interpolation methods. c. Using the discount factor curve from the log-linear interpolation, compute the price of a 5-year, 1% semiannual coupon bond and convert the price using Formula 2,5 to a semiannual yield. Do the same with a semiannual coupon rate of 8% to observe the coupon effect on yields. Hint: See Table 2.5 TABLE 2.5 Hint for bootstrap problem. 0.5 *** 2 7.5 0% 1.375% 2.125% 2.5% 3% 3.25% 9.5 10 Linear Zero rate Log-linear Zero rate DF DF 1 1 0.9962083 0.761% 0.9962083 0.761% 0.9724397 1.402% 0.9724406 1.402% 99.62083% 99.95086% 100.36222% 100% 100.62942% 100.42501% 0.7987633 3.018 % 0.7980435 3.031% 0.7373020 3.234 % 0.7366574 3.243% 0.7219367 3.285 % 0.7220633 3.283% FORMULA Pz(y, N, m) = D(T) = 1 (1+y/m)N-w (2.8) P(C, y, N,m) = P = N C/m 1 (1+y/m)i (1+y/m)N + i=1 1 1 = = ( -+y/my) + (1+y/m}\\ 1 y (2.5)
Step by Step Solution
3.45 Rating (155 Votes )
There are 3 Steps involved in it
To calculate the semiannual discount factors using the bootstrap method with linear and loglinear interpolation we start with the shortest maturity instrument 6month TBill and work our way up to the l... View full answer

Get step-by-step solutions from verified subject matter experts


