GIVEN TEMPLATE:

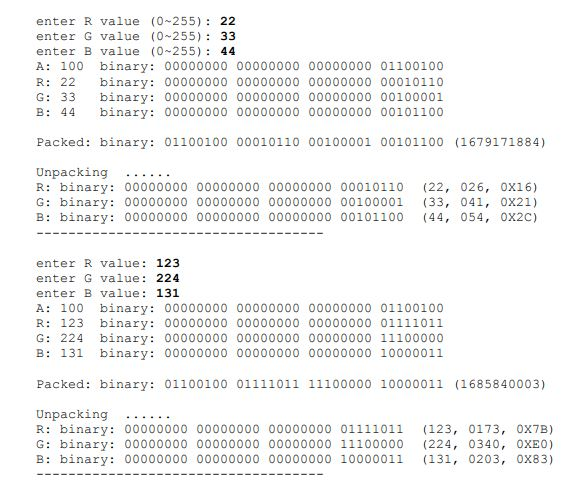
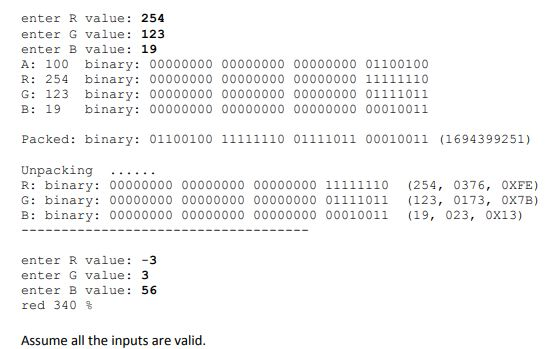
#include  #define AlphaValue 100 int main() { int r, g,b; unsigned int rgb_pack; int r_unpack, g_unpack,b_unpack; int alpha = AlphaValue; printf("enter R value (0~255): "); scanf("%d",&r); printf("enter G value (0~255): "); scanf("%d",&g); printf("enter B value (0~255): "); scanf("%d",&b); while(! (r  3.1 Specification A digital image is typically stored in computer by means of its pixel values, as well as some formatting information. Each pixel value consists of 3 values of 0 255, representing red (R) green (G) and blue (B). As mentioned in class, Java's Bufferedlmage class has a method int getRGB (int x,int y), which allows you to retrieve the RGB value of an image at pixel position (x, y). How could the method return 3 values at a time? As mentioned in class, the trick' is to return an integer (32 bits) that packs the 3 values into it. Since each value is 0 255 thus 8 bit is enough to represent it, an 32 bits integer has sufficient bits. They are packed in such a way that, counting from the right most bit, B values occupies the first 8 bits (bit 07), G occupies the next 8 bits, and R occupies the next 8 bits. This is shown below. (The left-most 8 bits is packed with some other information about the image, called Alpha, which we are not interested here.) 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 1 09 8 7 6 5 4 3 20 Suppose a pixel has R value 2 (which is binary 00000010), G value 7 (which is binary 00000111) and B value 8 (which is binary 00001000), and Alpha has value 100, then the integer is packed as 01011|01110111010101010101011|!! 1|1|010101011101010 100 for Alpha 3.2 Implementation In this exercise, you are going to use bitwise operations to pack input R,G and B values into an integer, and then use bitwise operations again to unpack the packed integer to retrieve the R, G and B values Download and complete lab3RGB.c. This C program keeps on reading input from the stdin Each input contains 3 integers representing the R, G and B value respectively, and then outputs the 3 values with their binary representations. The binary representations are generated by calling function void printBinary (int val), which is defined for you in another program binaryFunction.c. (How do you use a function that is defined in another file?) Next is the pack part that you should implement. This packs the 3 input values, as well as Alpha value which is assumed to be 100, into integer variable rgb pack Then the value of rgb_pack and its binary representation is displayed (implemented for you) Next you should unpack the R, G and B value from the packed integer rgb pack. After that, the unpacked R,G and B value and their Binary, Octal and Hex representations are displayed (implemented) The program terminates when you enter a negative number for either R, G or B value Hint: Packing might be a little easier than unpacking. Considering shifting R,G,B values to the proper positions and then somehow merge them into one integer (how about bitwise OR?). For unpacking, you can either do shifting+ masking, or, masking + shifting, or, shifting only. Shifting + masking means you first shift the useful bits to the proper positions, and then turn off (set to 0) the unwanted bits while keeping the values of the useful bits. What you want, for example for R value, is a binary representation of the following, which has decimal value 2 00 o 00 0 0 0 0 0 0 0 0 0 0 0 00 0 0l 0l ol 0 0 0 O 00l 001O Masking +shifting means you first use & to turn off some unrelated bits and keep the values of the good bits, and then do a shifting to move the useful bits to the proper position. Explore different approaches for unpacking Masking shifting means you first use & to turn off some unrelated bits and keep the values of the good bits, and then do a shifting to move the useful bits to the proper position. Explore different approaches for unpacking. Finally, it is interesting to observe that function printBinary () itself uses bitwise operations to generate artificial '0' or '1'. It is recommended that, after finishing this lab, you take a look at the code of printBinary yourself 3.3 Sample Inputs/Outputs red 339 % .out enter R value: 1 enter G value: 3 enter B value: 5 A: 100 binary: 00000000 00000000 00000000 01100100 G: 3 B:5 binary: 00000000 00000000 00000000 00000001 binary: 00000000 00000000 00000000 00000011 binary: 00000000 00000000 00000000 00000101 Packed binary 01100100 00000001 00000011 00000101 (1677787909) Unpacking .. R: binary: 00000000 00000000 00000000 00000001 ,01,0x1) G: binary: 00000000 00000000 00000000 00000011 (3, 03, 0X3) B: binary: 00000000 00000000 00000000 00000101 (5,05, 0x5) enter R value (0 255) 22 enter G value (0255) 33 enter B value (0 255) 44 A: 100 binary: 00000000 00000000 00000000 01100100 R: 22 binary: 00000000 00000000 00000000 00010110 G: 33 binary: 00000000 00000000 00000000 00100001 B: 44 binary: 00000000 00000000 00000000 00101100 Packed: binary: 01100100 00010110 00100001 00101100 (1679171884) Unpacking R: binary: 00000000 00000000 00000000 00010110 (22, 026, 0x16) G: binary: 00000000 00000000 00000000 00100001 (33, 041, 0X21) B: binary 00000000 00000000 00000000 00101100 (44, 054, 0X2C) enter R value: 123 enter G value: 224 enter B value: 131 A: 100 binary: 00000000 00000000 00000000 01100100 R 123 binary: 00000000 00000000 00000000 01111011 G: 224 binary: 00000000 00000000 00000000 11100000 B: 131 binary: 00000000 00000000 00000000 10000011 Unpacking R: binary: 00000000 00000000 00000000 01111011 (123, 0173, 0X7B) G: binary 00000000 00000000 00000000 11100000 (224, 0340, OXEO) B: binary: 00000000 00000000 00000000 10000011 (131, 0203, 0x83) enter R value: 254 enter G value: 123 enter B value 19 A: 100 binary: 00000000 00000000 00000000 01100100 R: 254 binary 00000000 00000000 00000000 11111110 G 123 binary: 00000000 00000000 00000000 01111011 B: 19 binary: 00000000 00000000 00000000 00010011 Unpacking R binary: 00000000 00000000 00000000 11111110 (254, 0376, 0XFE) G: binary 00000000 00000000 00000000 01111011 (123, 0173, 0X7B) B: binary: 00000000 00000000 00000000 00010011 (19, 023, 0X13) enter R value: -3 enter G value: 3 enter B value: 56 red 340 % Assume all the inputs are valic