Question
Given the following conversion of the spot interest rate R(t, T): Please prove that whether you use periodic compounding or continuous compounding, the relationship between
Given the following conversion of the spot interest rate R(t, T):
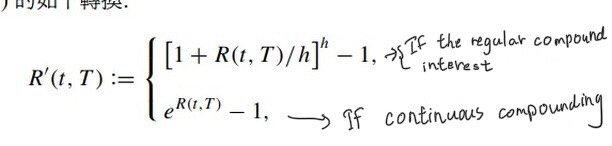
Please prove that whether you use periodic compounding or continuous compounding, the relationship between the discount factor B(t, T) and the spot interest rate 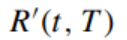 can be simplified as:
can be simplified as:
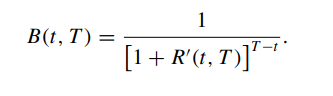
Please derive another conversion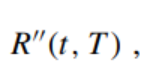 of the spot interest rate R(t, T), so that whether it is using periodic compounding or continuous compounding, the discount factor B(t, T) and the spot interest rate
of the spot interest rate R(t, T), so that whether it is using periodic compounding or continuous compounding, the discount factor B(t, T) and the spot interest rate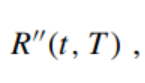 are:
are:
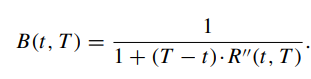
Please derive another conversion 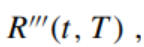 of the spot interest rate R(t, T ), so that whether it is using periodic compounding or continuous compounding, the discount factor B(t, T) and the spot interest rate
of the spot interest rate R(t, T ), so that whether it is using periodic compounding or continuous compounding, the discount factor B(t, T) and the spot interest rate 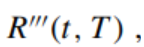 are:
are:
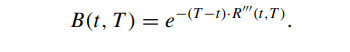
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


