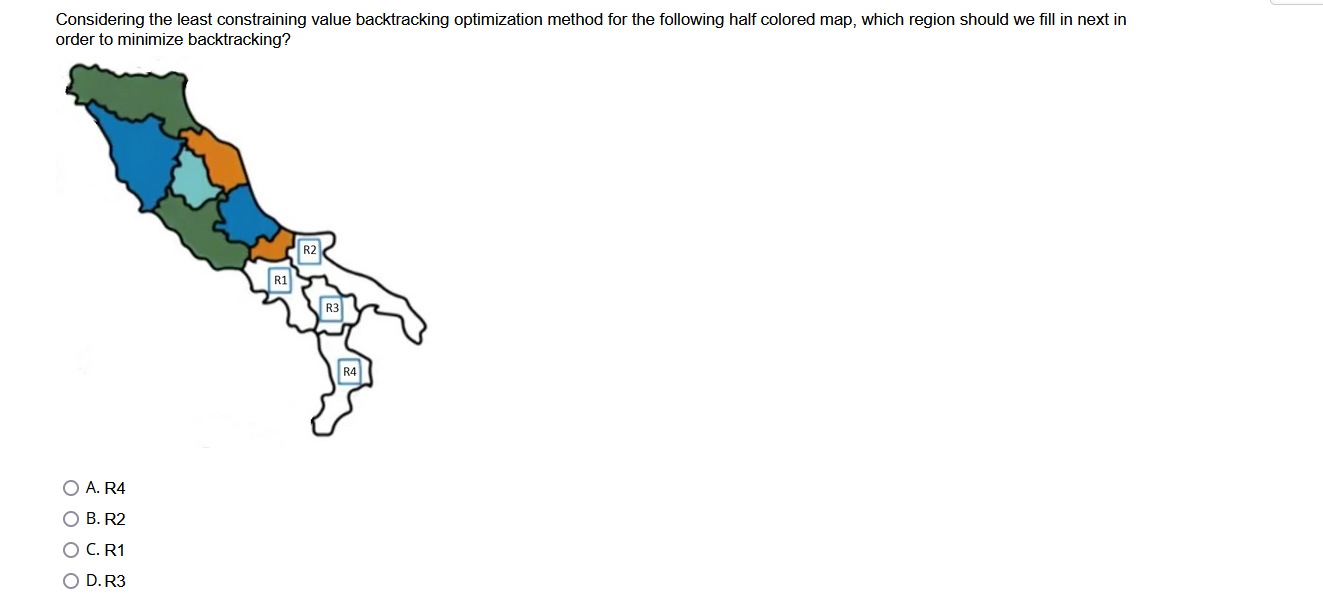
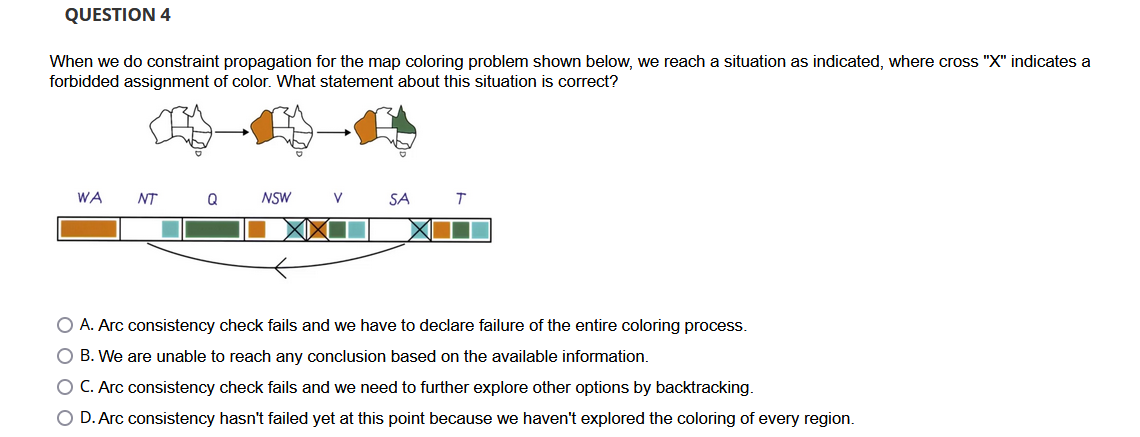
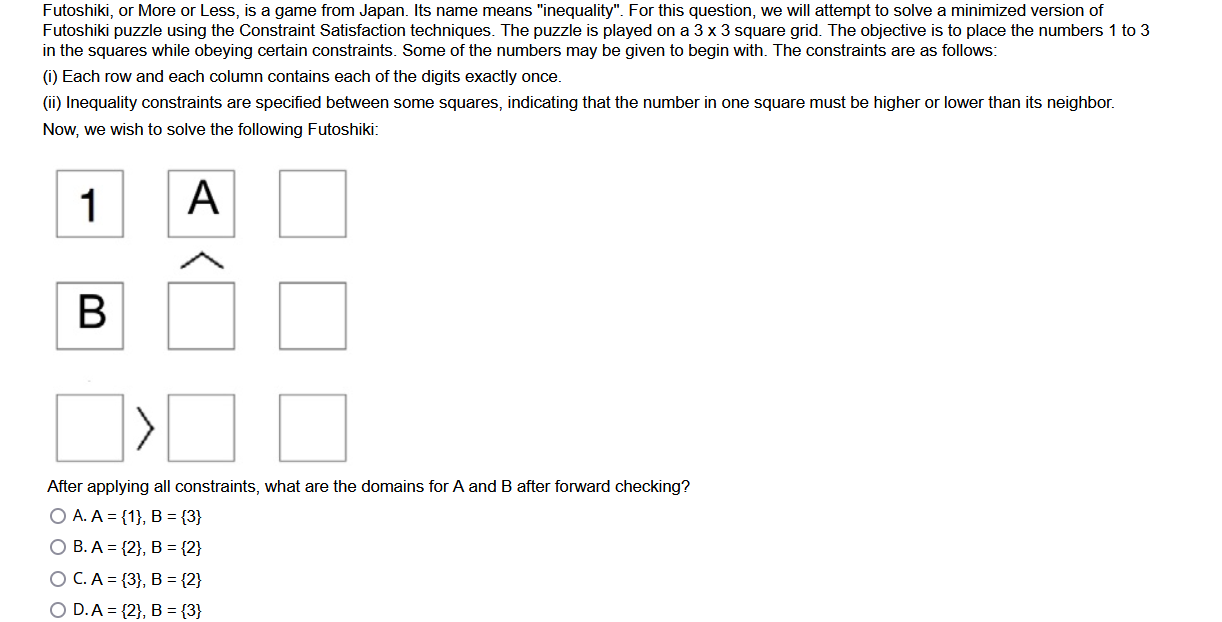
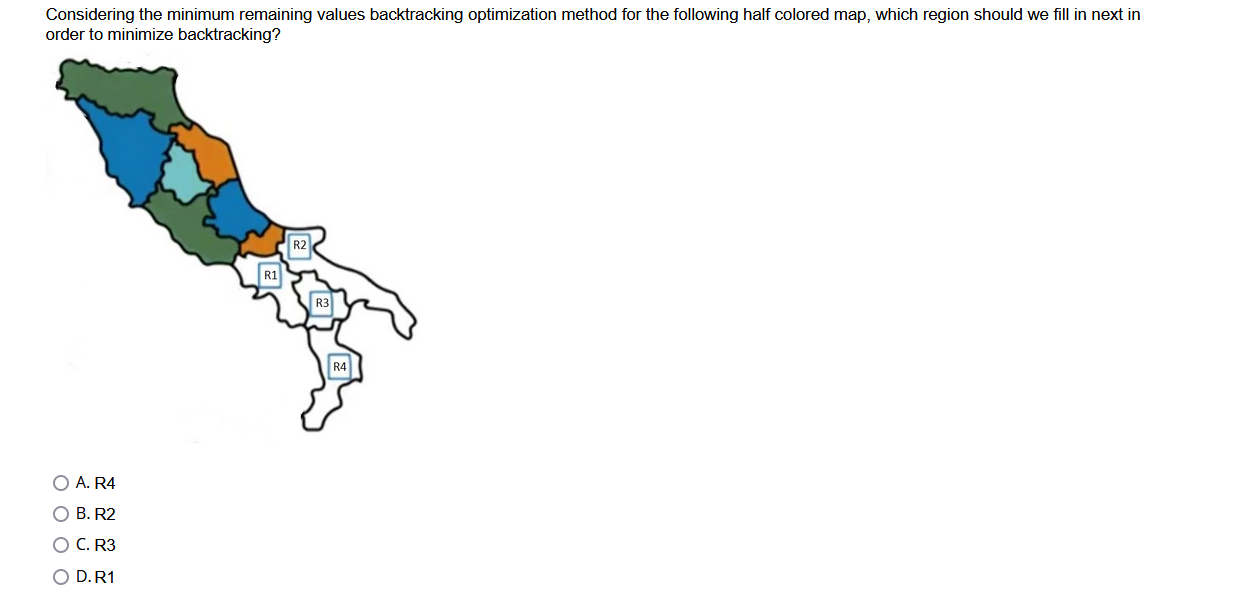
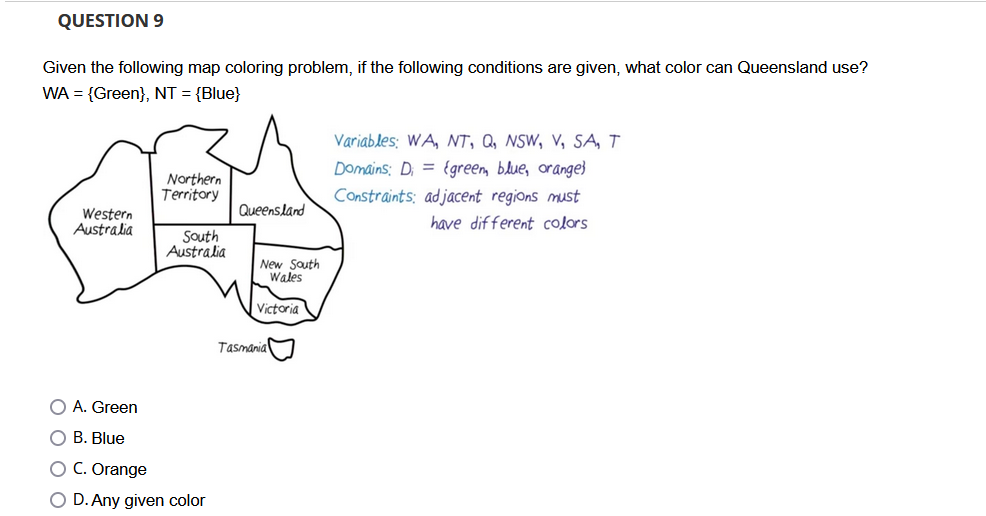
Given the following map coloring problem and the result of constraint propagation and forward checking, where a check mark indicates that the corresponding color is a feasible option for coloring the region, is the entire network arc consistent? True False Futoshiki, or More or Less, is a game from Japan. Its name means "inequality". For this question, we will attempt to solve a minimized version of Futoshiki puzzle using the Constraint Satisfaction techniques. The puzzle is played on a 33 square grid. The objective is to place the numbers 1 to 3 in the squares while obeying certain constraints. Some of the numbers may be given to begin with. The constraints are as follows: (i) Each row and each column contains each of the digits exactly once. (ii) Inequality constraints are specified between some squares, indicating that the number in one square must be higher or lower than its neighbor. Now, we wish to solve the following Futoshiki: After applying all constraints, what are the domains for A and B after forward checking? A. A={2},B={3} B. A={},B={} i.e., no solution C. A={2},B={2} D. A={3},B={2} Considering the least constraining value backtracking optimization method for the following half colored map, which region should we fill in next in order to minimize backtracking? A. R4 B. R2 C. R1 D. R3 When we do constraint propagation for the map coloring problem shown below, we reach a situation as indicated, where cross "X" indicates a forbidded assignment of color. What statement about this situation is correct? A. Arc consistency check fails and we have to declare failure of the entire coloring process. B. We are unable to reach any conclusion based on the available information. C. Arc consistency check fails and we need to further explore other options by backtracking. D. Arc consistency hasn't failed yet at this point because we haven't explored the coloring of every region. Futoshiki, or More or Less, is a game from Japan. Its name means "inequality". For this question, we will attempt to solve a minimized version of Futoshiki puzzle using the Constraint Satisfaction techniques. The puzzle is played on a 33 square grid. The objective is to place the numbers 1 to 3 in the squares while obeying certain constraints. Some of the numbers may be given to begin with. The constraints are as follows: (i) Each row and each column contains each of the digits exactly once. (ii) Inequality constraints are specified between some squares, indicating that the number in one square must be higher or lower than its neighbor. Now, we wish to solve the following Futoshiki: After applying all constraints, what are the domains for A and B after forward checking? A. A={1},B={3} B. A={2},B={2} C. A={3},B={2} D. A={2},B={3} Considering the minimum remaining values backtracking optimization method for the following half colored map, which region should we fill in next in order to minimize backtracking? A. R4 B. R2 C. R3 D. R1 Given the following map coloring problem, what color can Tasmania use? iables: WA, NT, Q, NSW, V, SA, T nains: Di= (greem, blue, orange) istraints: adjacent regions must have different colors A. Green B. Blue C. Orange Given the following arithmetic problem and a constraint hypergraph for the problem where the top square represents the global constraint that all the letters have to be different. In addition, we know that O+O has to be equal to R+10 times X, where X1 represents the carry to the tens place and it can be 0 or 1 . Similarly, x1+W+W has to equal U+10 times x2, where x2 represents the carry to the hundredth place. We also know that F has to equal X3, where X3 represents the carry to the thousandth place. How do we express the constraint that the problem does not allow leading 0's? Variables: FTWRO123 Domains: (D,1,2,3,4,5,6,7,8,9) Constraints: alldiff (F,T,U,W,R,0) O+O=R+10x1 x1+W+W=U+10x2+T+T=x3=F A. F=1 B. T!=0 and F!=0 C. F!=0 D. x2+T+T=O+10x3 Given the following map coloring problem, if the following conditions are given, what color can Queensland use? rriables: WA1NT,Q,NSW,V,SA1T imains: Di= (greem, blue, orange) Instraints: adjacent regions must have different colors A. Green B. Blue C. Orange D. Any given color Given the following arithmetic problem and a constraint hypergraph for the problem where the top square represents the global constraint that all the letters have to be different. In addition, we know that O+O has to be equal to R+10 times X1, where X1 represents the carry to the tens place and it can be 0 or 1 . Similarly, x1+W+W has to equal U+10 times x2, where x2 represents the carry to the hundredth place. We also know that F has to equal X3, where X3 represents the carry to the thousandth place. Complete the equation for T+T Variables: FTUWRO123 Domains: (0,1,2,3,4,5,6,7,8,9) Constraints: alldiff (F,T,U,W,R,O) 0+0=R+10X1 x1+W+W=U+10x2C3+T+T=x3=F A. T+T=O+103 B. x1+T+T=0+10x2 C. x2+T+T=10x3 D. x2+T+T=O+10x3