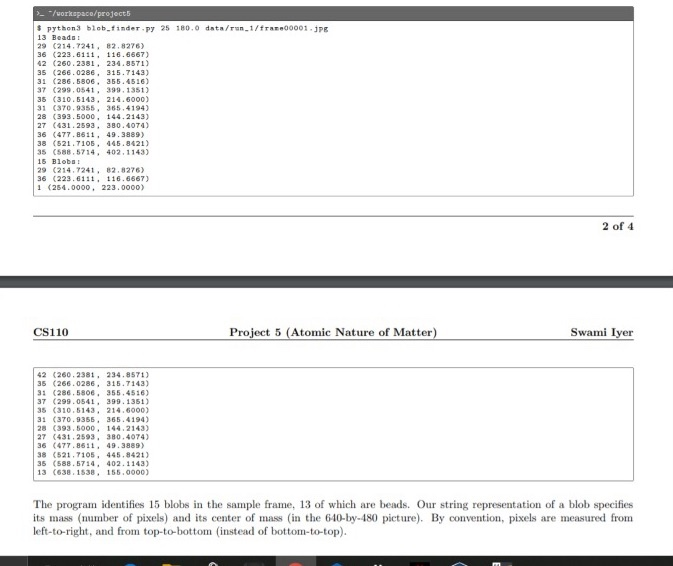
Goal The purpose of this project is to re-affirm the atomic nature of matter by tracking the motion of particles undergoing Brownian motion, fitting this data to Einstein's model, and estimating Avogadro's constant. Background The atom played a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of wildflower pollen grains immersed in water using a microscope. This motion would later become known as Brownian motion. Einstein hypothesized that this Brownian motion was the result of millions of tiny water molecules colliding with the larger pollen grain particles. In one of his "miracle year" (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the "existence of atoms of definite finite size." His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein's kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. His experiment also provided one of the earliest estimates of Avogadro's constant. For this work, Perrin won the 1926 Nobel Prize in physics. The Problem In this project, you will redo a version of Perrin's experiment. Your job is greatly simplified because with modern video and computer technology (in conjunction with your programming skills), it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres ("beads") suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein's model, and estimate Avogadro's constant. Here is a movie avi .mov ) of several beads undergoing Brownian motion. Below is a typical raw image (left) and a cleaned up version (right) using thresholding, as described below. Each image shows a two-dimensional cross section of a microscope slide. The beads move in and out of the microscope's field of view the 2- and y-directions). Beads also move in the 2-direction, so they can move in and out of the microscope's depth of focus this results in halos, and it can also result in beads completely disappearing from the image. Problem 2. (Particle Identification) The first challenge is to identify the beads amidst the noisy data. Each image is 640-by-480 pixels, and each pixel is represented by a color object which needs to be converted to a luminance value ranging from 0.0 (black) to 255.0 (white). Whiter pixels correspond to beads (foreground) and blacker pixels to water (background) We break the problem into three pieces: 1. Read the image. Use the Picture data type to read in the image. 2. Classify the pirels as foreground or background. We use a simple, but effective, technique known as thresholding to separate the pixels into foreground and background components: all pixels with monochrome luminance values strictly below some threshold 7 (tau) are considered background, and all others are considered foreground. The two pictures in figure above illustrate the original frame (left) and the same frame after thresholding (right), using T=180.0. This value of results in an effective cutoff for the supplied data. 3. Find the blobs. A polystyrene bead is typically represented by a disc-like shape of at least some minimum number pixels (typically 25) of connected foreground pixels. A blob or connected component is a maximal set of connected foreground pixels, regardless of its shape or size. We will refer to any blob containing at least pixels number of pixels as a bead. The center-of-mass of a blob (or bead) is the average of the r- and y-coordinates of its constituent pixels. Define a data type called Blobfinder in blob finder.py that supports the following API. Use depth-first search to efficiently identify the blobs. Method BlobFinder (pic, tau) bf.getBeade (pixels) Description constructs a blob finder bf to find blobs in the picture pic using a luminance threshold tau returns a list of all beads with mass pixels > "/workspace/projects $ python3 blob_finder.py 25 180.0 data/run_1/fra 00001.jpg 13 Beads 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 42 (260, 281, 234.8571) 35 (266.0286, 315.7143) 31 (286.5806 355.4516) 37 (299. 0541 399.1351) 35 (310.5143, 214.5000) 33370.9355 365.4194 (393.5000, 144.2143) 27 (431.2593, 380,4074) 36 (477.8511, 49.3889) 30 (521, 7105 445.8421) (588.5714, 402.1143) 15 Blobat 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 1 (254.0000 223.0000) 2 of 4 >_/workspace/projects $ python3 blob_finder.py 25 180.0 data/re_1/trac00001.jpg 13 Beador 29 (214.7241.82.8276) 36 (223.6111, 116.6667) 42 (260.238, 234.8571) 35 (266.0286315.7143) 31 (286.5806. 255. 4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.5000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431, 2593 280.4074) 36 (477.8511, 49.3889) 38 (521.7105, 145.8421) 35 (588.5714, 402.1143) (214.7241, 82.8276) 36 (223.6111, 116.6667) 1 (254.0000, 223.0000) 2 of 4 CS110 Project 5 (Atomic Nature of Matter) Swami Iver 42 (260.2381 234.8571) 35 (266. 0286, 315.7143) 3: (286.5806 355.4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.6000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431.2593 380.4074) 36 (477.8511, 49.3889) 38 (521.7105, 445.8421) 35 (588.5714, 402.1143) 13 (638. 1538, 155.0000) The program identifies 15 blobs in the sample frame, 13 of which are beads. Our string representation of a blob specifies its mass number of pixels) and its center of mass in the 640-by-480 picture). By convention, pixels are measured from left-to-right, and from top-to-bottom (instead of bottom-to-top). Goal The purpose of this project is to re-affirm the atomic nature of matter by tracking the motion of particles undergoing Brownian motion, fitting this data to Einstein's model, and estimating Avogadro's constant. Background The atom played a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of wildflower pollen grains immersed in water using a microscope. This motion would later become known as Brownian motion. Einstein hypothesized that this Brownian motion was the result of millions of tiny water molecules colliding with the larger pollen grain particles. In one of his "miracle year" (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the "existence of atoms of definite finite size." His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein's kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. His experiment also provided one of the earliest estimates of Avogadro's constant. For this work, Perrin won the 1926 Nobel Prize in physics. The Problem In this project, you will redo a version of Perrin's experiment. Your job is greatly simplified because with modern video and computer technology (in conjunction with your programming skills), it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres ("beads") suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein's model, and estimate Avogadro's constant. Here is a movie avi .mov ) of several beads undergoing Brownian motion. Below is a typical raw image (left) and a cleaned up version (right) using thresholding, as described below. Each image shows a two-dimensional cross section of a microscope slide. The beads move in and out of the microscope's field of view the 2- and y-directions). Beads also move in the 2-direction, so they can move in and out of the microscope's depth of focus this results in halos, and it can also result in beads completely disappearing from the image. Problem 2. (Particle Identification) The first challenge is to identify the beads amidst the noisy data. Each image is 640-by-480 pixels, and each pixel is represented by a color object which needs to be converted to a luminance value ranging from 0.0 (black) to 255.0 (white). Whiter pixels correspond to beads (foreground) and blacker pixels to water (background) We break the problem into three pieces: 1. Read the image. Use the Picture data type to read in the image. 2. Classify the pirels as foreground or background. We use a simple, but effective, technique known as thresholding to separate the pixels into foreground and background components: all pixels with monochrome luminance values strictly below some threshold 7 (tau) are considered background, and all others are considered foreground. The two pictures in figure above illustrate the original frame (left) and the same frame after thresholding (right), using T=180.0. This value of results in an effective cutoff for the supplied data. 3. Find the blobs. A polystyrene bead is typically represented by a disc-like shape of at least some minimum number pixels (typically 25) of connected foreground pixels. A blob or connected component is a maximal set of connected foreground pixels, regardless of its shape or size. We will refer to any blob containing at least pixels number of pixels as a bead. The center-of-mass of a blob (or bead) is the average of the r- and y-coordinates of its constituent pixels. Define a data type called Blobfinder in blob finder.py that supports the following API. Use depth-first search to efficiently identify the blobs. Method BlobFinder (pic, tau) bf.getBeade (pixels) Description constructs a blob finder bf to find blobs in the picture pic using a luminance threshold tau returns a list of all beads with mass pixels > "/workspace/projects $ python3 blob_finder.py 25 180.0 data/run_1/fra 00001.jpg 13 Beads 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 42 (260, 281, 234.8571) 35 (266.0286, 315.7143) 31 (286.5806 355.4516) 37 (299. 0541 399.1351) 35 (310.5143, 214.5000) 33370.9355 365.4194 (393.5000, 144.2143) 27 (431.2593, 380,4074) 36 (477.8511, 49.3889) 30 (521, 7105 445.8421) (588.5714, 402.1143) 15 Blobat 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 1 (254.0000 223.0000) 2 of 4 >_/workspace/projects $ python3 blob_finder.py 25 180.0 data/re_1/trac00001.jpg 13 Beador 29 (214.7241.82.8276) 36 (223.6111, 116.6667) 42 (260.238, 234.8571) 35 (266.0286315.7143) 31 (286.5806. 255. 4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.5000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431, 2593 280.4074) 36 (477.8511, 49.3889) 38 (521.7105, 145.8421) 35 (588.5714, 402.1143) (214.7241, 82.8276) 36 (223.6111, 116.6667) 1 (254.0000, 223.0000) 2 of 4 CS110 Project 5 (Atomic Nature of Matter) Swami Iver 42 (260.2381 234.8571) 35 (266. 0286, 315.7143) 3: (286.5806 355.4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.6000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431.2593 380.4074) 36 (477.8511, 49.3889) 38 (521.7105, 445.8421) 35 (588.5714, 402.1143) 13 (638. 1538, 155.0000) The program identifies 15 blobs in the sample frame, 13 of which are beads. Our string representation of a blob specifies its mass number of pixels) and its center of mass in the 640-by-480 picture). By convention, pixels are measured from left-to-right, and from top-to-bottom (instead of bottom-to-top)