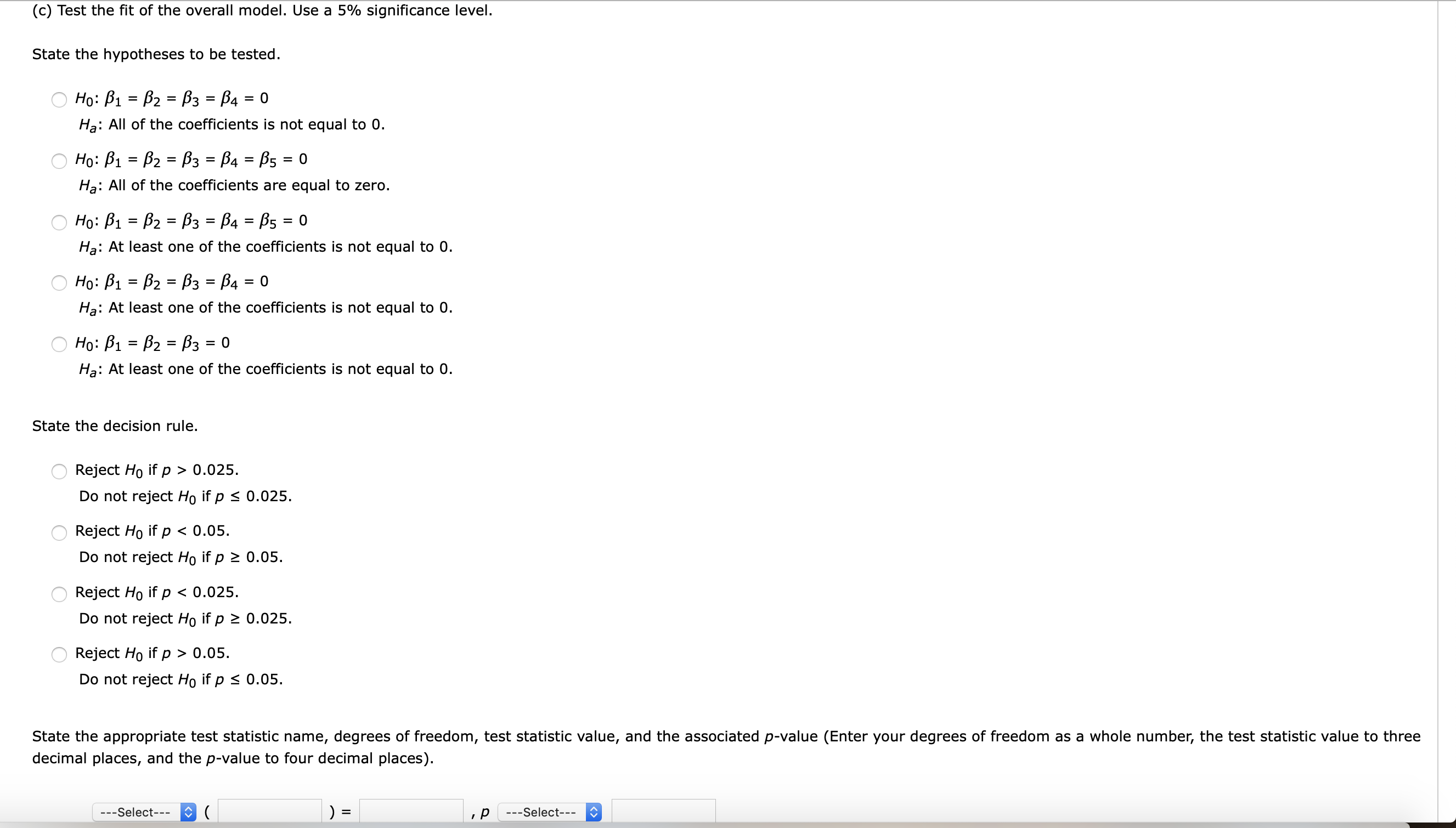
Graduate School Admission: UGA wishes to build a model to classify graduate school applicants into two groups: Those who are qualied and should be admitted and those who are not qualified and should not be admitted. The applicants in the sample data were reviewed using traditional means (i.e., application, statement of purpose, and essays reviewed by an expert panel of admissions officers) and scored "Yes" to be admitted or "No" not to be admitted. The available variables are contained in the worksheet "Admissions" and dened as follows. Admit: Coded as "Yes" if the applicant is to be admitted and "No" otherwise. GRE: The applicant's score of the Graduate Record Examination (GRE). GPA: The applicant's undergraduate GPA. Rank: The ranking (1-4) of the applicant's undergraduate institution. Fit the proper regression model to predict the variable Admit. Fit the model so that the event being modeled is \"Yes" for the variable Admit. Furthermore, treat the variable Rank as a categorical predictor variable and code it so that Rank #1 serves as the reference group. (a) Complete the following statement (Enter your first answer as a whole number and the percent rounded to two decimal places). Out of a total of n = applicants in the sample, % were admitted. (b) State the model equation. A )7 = o+l(GRE)+2(GPA)+3(Rank1)+[34(Rank2)+[35(RanIG) 1 1+e(lio+B1(GRE)+BZ(GPA)+133(Rank1)+4(RankZ)+lis(Rank3)) 1 1+e(o+l(GRE)+Z(GPA)+Ba(Rank2)+4(Rank3)+[35(Rank4)) d P(Y = Admitted) = f\" P(Y = Admitted) = r\" V = 50+I'1(GRE)+l32(GPA)+/33(Rank) '7' l7 = o+1(GRE)+2(GPA)+3(Rank2)+4(Rank3)+5(Rank4) 1 'A' P" = Admitted) = 1+e-(o+B1(GRE)+z(GPA)+3(Rank)) (c) Test the fit of the overall model. Use a 5% significance level. State the hypotheses to be tested. O Ho: B1 = B2 = B3 = B4 = 0 Ha: All of the coefficients is not equal to 0. O Ho: B1 = B2 = B3 = B4 = $5 = 0 Ha: All of the coefficients are equal to zero. O Ho: B1 = B2 = B3 = B4 = $5 = 0 Ha: At least one of the coefficients is not equal to 0. O Ho: B1 = B2 = P3 = B4 = 0 Ha: At least one of the coefficients is not equal to 0. O Ho: B1 = $2 = 3 = 0 Ha: At least one of the coefficients is not equal to 0. State the decision rule. O Reject Ho if p > 0.025. Do not reject Ho if p S 0.025. Reject Ho if p 0.05. Do not reject Ho if p s 0.05. State the appropriate test statistic name, degrees of freedom, test statistic value, and the associated p-value (Enter your degrees of freedom as a whole number, the test statistic value to three decimal places, and the p-value to four decimal places). ---Select--- ( ) = P ---Select--- E