graph referenced by part a
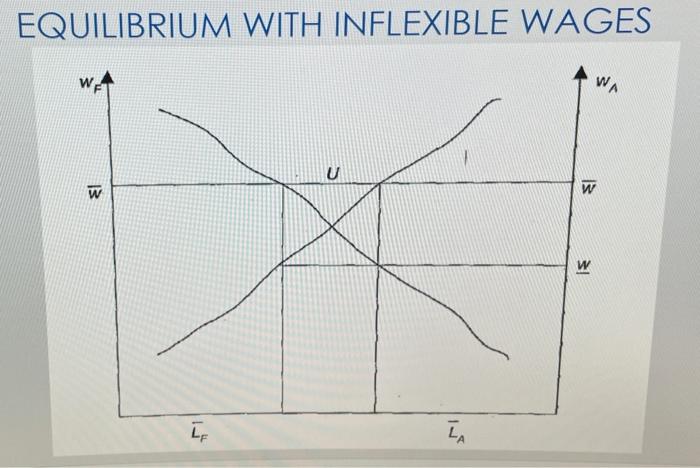
2. Harris-Todaro Model. Harrisville's economy operates according to the Harris-Todaro model. The total labor supply is 50. (You can think of the 50 as representing 50 thousand people, so that non- integer answers are meaningful) Rural labor demand is: WALA) = 50 LA. Urban labor demand is: W:(Lt) - 50/L Draw a graph like the one from Lecture 16 slide 19 showing the equilibrium in Harrisville is wages are flexible How much labor works in agriculture? How much in manufacturing? What is the wage in each sector? You can solve this graphically and/or using the fact that, in an equilibrium with flexible wages, wages must be equal in both sectors, or workers will migrate from one to the other. Remember that there is no unemployment when wages are flexible, so LA-S0 LM 6. Now imagine that urban wages fixed at 1. That is: W:(Lt) =W= 4. How much labor does the manufacturing sector employ at this wage? If the agriculture sector paid the same wage (that is. We = 4). how much labor would it employ? How much labor would be unemployed? d. Check whether the situation described in parts bande is an equilibrium. That is, plug the values of W. Ws. Lx and Lu that you found into the migration equilibrium equation: WA- WsL. (La + Lu) and see if the equation holds Now check whether there is an equilibrium (with unemployment) where LA-25 and Ly = 12.5.(W., so that tells you that Lat is the value you found in part b.) You must plug the values of W. Ws, Ls and Lu into the migration equilibrium equation and check whether it holds to get full credit. c. e EQUILIBRIUM WITH INFLEXIBLE WAGES WA U w is is LE TA 2. Harris-Todaro Model. Harrisville's economy operates according to the Harris-Todaro model. The total labor supply is 50. (You can think of the 50 as representing 50 thousand people, so that non- integer answers are meaningful) Rural labor demand is: WALA) = 50 LA. Urban labor demand is: W:(Lt) - 50/L Draw a graph like the one from Lecture 16 slide 19 showing the equilibrium in Harrisville is wages are flexible How much labor works in agriculture? How much in manufacturing? What is the wage in each sector? You can solve this graphically and/or using the fact that, in an equilibrium with flexible wages, wages must be equal in both sectors, or workers will migrate from one to the other. Remember that there is no unemployment when wages are flexible, so LA-S0 LM 6. Now imagine that urban wages fixed at 1. That is: W:(Lt) =W= 4. How much labor does the manufacturing sector employ at this wage? If the agriculture sector paid the same wage (that is. We = 4). how much labor would it employ? How much labor would be unemployed? d. Check whether the situation described in parts bande is an equilibrium. That is, plug the values of W. Ws. Lx and Lu that you found into the migration equilibrium equation: WA- WsL. (La + Lu) and see if the equation holds Now check whether there is an equilibrium (with unemployment) where LA-25 and Ly = 12.5.(W., so that tells you that Lat is the value you found in part b.) You must plug the values of W. Ws, Ls and Lu into the migration equilibrium equation and check whether it holds to get full credit. c. e EQUILIBRIUM WITH INFLEXIBLE WAGES WA U w is is LE TA

 graph referenced by part a
graph referenced by part a





