Graph Theory Question

Partial solution:

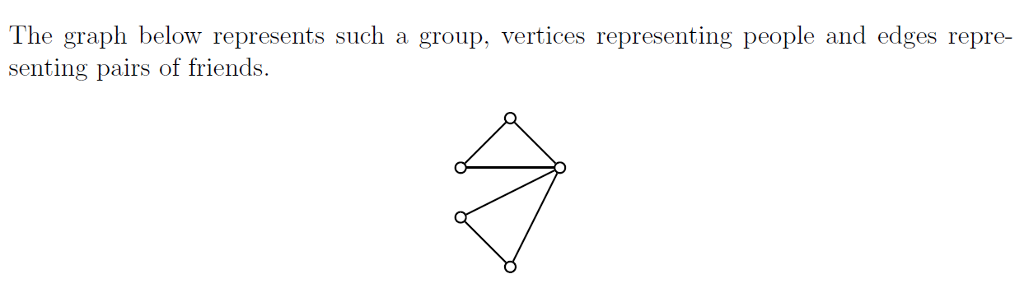
Have you looked at how many "friends" each pair has in common? Lets call the three people making up the top triangle "A", "B", and "C" where "A" is the top vertex and we go counter-clockwise so that "C" is that vertex with all 4 other people as friends. Call the last two "D" and "E" again going counter-clockwise around that lower triangle. Now, who are each persons friends? A has B and C as friends B has A and C as friends C has A, B, D, and E as friends D has C and E as friends E has C and D as friends Now look at the 10 pairs: A and B have C as a common friend A and C have B as a common friend A and D have C as a common friend A and E have C as a common friend B and C has A as a common friend B and D have C as a common friend B and E have C as a common friend C and D have E as a common friend C and E have D as a common friend D and E have C as a common friend

There are 10 possible edges in the graph. There are 2^10 = 1024 2^10=1024 possible graphs on five vertices. That is a finite collection of graphs. You want to show that only the graphs that look like your drawing fit the criteria that any two vertices have edges to exactly one common vertex. Out of the 1024 graphs, I believe 120 of them look like the graph you show as the solution. So, does this need to be "fully justied"? That might be a considerably larger amount of work. You could justify it by analyzing all of the 1024 graphs and showing that only the 120 graphs that look like the graph shown as a solution are correct. Or, you can assume that you have a valid graph representing this group of five friends and start analyzing it. Choose two people. Label them A,B. We know they share exactly one friend in common. Call that friend C. We now have edges AC and BC. If we consider A and C, we know they share exactly one friend. So, we have the following possibilities: Case 1: B is the common friend Case 2: D is the common friend Case 3: E is the common friend

Then consider B and C. Case 1: A is the common friend Case 2: D is the common friend Case 3: E is the common friend. Keep going until you fully explain the entire graph and all possible permutations.

escribe a group of five people, any two of whom have exactly one friend in common escribe a group of five people, any two of whom have exactly one friend in common