Hello, can you help me to solve this question in code by using Python? Also, ignore 2.3. Thank you so much!!

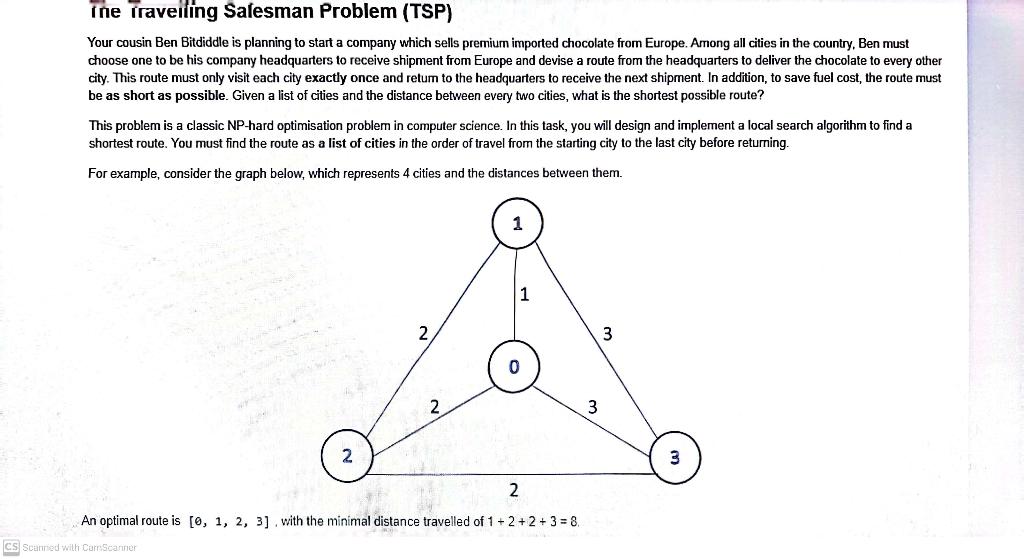
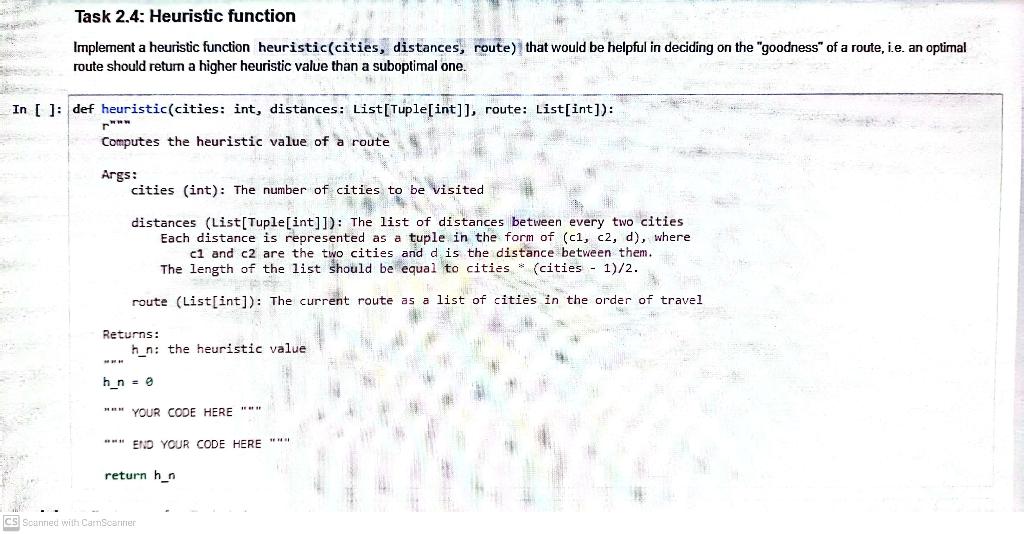
Ine iraveiling Safesman Problem (TSP) Your cousin Ben Bitdiddle is planning to start a company which sells premium imported chocolate from Europe. Among all cities in the country, Ben must choose one to be his company headquarters to receive shipment from Europe and devise a route from the headquarters to deliver the chocolate to every other city. This route must only visit each city exactly once and retum to the headquarters to receive the next shipment. In addition, to save fuel cost, the route must be as short as possible. Given a list of cities and the distance between every two cities, what is the shortest possible route? This problem is a classic NP-hard optimisation problem in computer science. In this task, you will design and implement a local search algorithm to find a shortest route. You must find the route as a list of cities in the order of travel from the starting city to the last city before returning. For example, consider the graph below, which represents 4 cities and the distances between them. An optimal route is [0,1,2,3], with the minimal distance travelled of 1+2+2+3=8. An optimal route is [0,1,2,3], with the minimal distance travelled of 1+2+2+3=8. Note: - There can be more than 1 shortest route, e.g., [1,0,3,2],[1,3,2,0], etc. You only need to find one such route. - [0,1,2] is not legal as the route must go through all 4 cities. - [0,1,2,3,1] is not legal as city 1 is visited more than once. - [1,3,0,2] is legal but it is not the shortest route, as the distance travelled of 3+3+2+2=10. Can you do better? Recall that similar to A search, local search utilises heuristics to decide when to transition from one state to another. However, being an uninformed guy, your cousin Ben Bitdiddle tells you to use the "greedy" solution. Given an incomplete route, the "greedy" solution builds a path by adding the closest unvisited node from the last visited node, until all nodes are visited. For instance, in the graph above, the "greedy" solution is [0,1,2,3]. Although this solution seems relatively sensible, as a CS2109S student, you have a nagging feeling that it may not work all the time. Can you create a heuristic and transition function to get better results with local search? Note: - For the following tasks, we will be benchmarking your hill-climbing algorithm against our own version using the greedy solution. Note that the hidden test cases can be quite large, so any brute-force solution will not suffice. - Your own transition and heuristic functions may underperform against the greedy solution for small instances of TSP, but should outperform the greedy solution consistently for large instances. For our public and private test cases, we have designed the greedy solution to be suboptimal. - If your code does not pass the private test cases on Coursemology because it underperforms against the greedy solution, you may re-run your code a few times in case you are "unlucky" with random initial routes. Task 2.3: State transitions Implement a reasonable transition function transition(route) to generate new candidate solutions. It should return a list of new routes to be used in the next iteration in the hill-climbing algorithm. Task 2.4: Heuristic function Implement a heuristic function heuristic(cities, distances, route) that would be helpful in deciding on the "goodness" of a route, i.e. an optimal route should return a higher heuristic value than a suboptimal one. def heuristic(cities: int, distances: List[Tuple[int]], route: List[int]): rn+m Computes the heuristic value of a route Args: cities (int): The number of cities to be visited distances (List[Tuple[int]]): The list of distances between every two cities Each distance is represented as a tuple in the form of (c1,c2,d), where c1 and c2 are the two cities and d is the distance between them. The length of the list should be equal to cities * (cities - 1)/2. route (List[int]): The current route as a list of cities in the order of travel Returns: hnn : the heuristic value hn=0 YOUR CODE HERE """ END YQUR CODE hERE "" return h_n \( \begin{aligned}]: & \text { F Test cose for Task } 2.4 \\ & \text { cities }=4 \\ & \text { distances }=[(1,0,10),(0,3,22),(2,1,8),(2,3,30),(1,3,25),(0,2,15)] \\ & \text { route_1 = heuristic(cities, distances, }[0,1,2,3]) \\ & \text { route_2 = heuristic(cities, distances, }[2,1,3,0]) \\ & \text { route_ } 3=\text { heuristic(cities, distances, }[1,3,2,0]) \\ & \text { print(route_1 = route,2) = True } \\ & \text { print(route_1 route, } 3)=\text { True }\end{aligned} \) CS Scanned with CamScanner