Hello! Could you help me solve these questions?

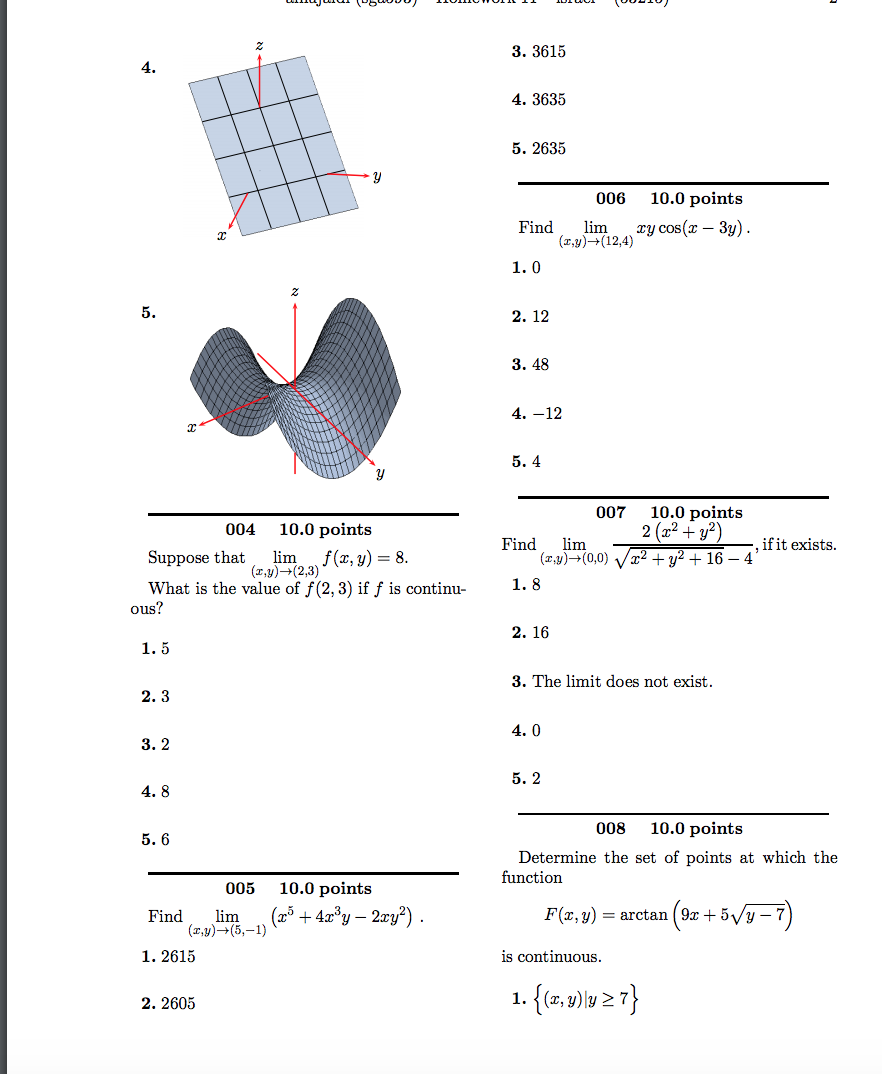
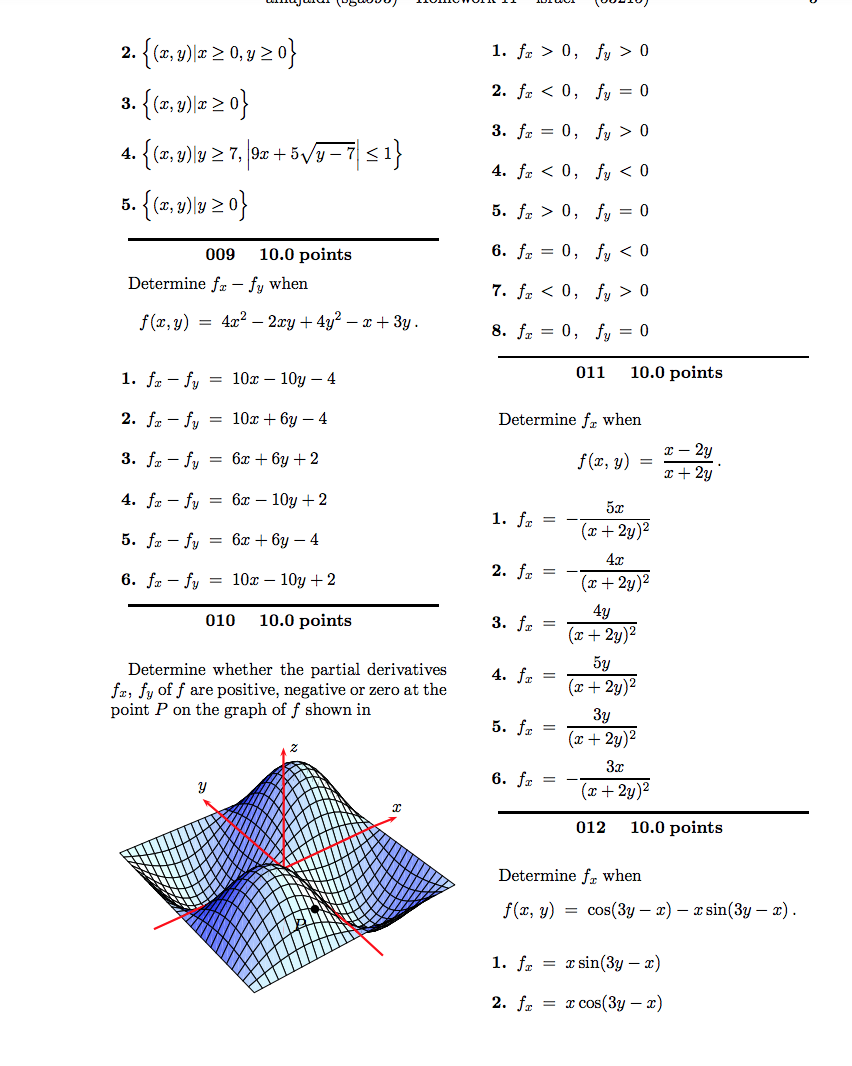
3. 3615 4. 4. 3635 5. 2635 006 10.0 points Find lim ry cos(x - 3y). (I,y)- (12,4) 1. 0 5. 2. 12 3. 48 4. -12 5. 4 007 10.0 points 004 10.0 points Find lim if it exists. Suppose that (1,y) -+(2,3) J (2, y) = 8. (r,y)-+(0,0) v/x2+y2+16 - What is the value of f(2, 3) if f is continu- 1. 8 ous? 2. 16 1. 5 3. The limit does not exist. 2. 3 4. 0 3. 2 5. 2 4. 8 5.6 008 10.0 points Determine the set of points at which the 005 10.0 points function Find (r,y)-+(5,-1) (# +4x y - 2xy?) F(x, y) = arctan (97 + 5\\/y -7) 1. 2615 is continuous. 2. 2605 1. ( x, y ) ly 27 }2. (z, y) | 2 20,320) 1. fx > 0, fy > 0 3. (x, y) 2 20} 2. fr 0 4. (x, y) ly 2 7, 92 + 5Vy -7 51} 4. fx 0, fy = 0 009 10.0 points 6. fx = 0, fy 0 f(x,y) = 4x2 -2xy + 4y? - x + 3y. 8. fx = 0, fy = 0 1. fx - fy = 10x - 10y - 4 011 10.0 points 2. fx - fy = 10x + 6y - 4 Determine fr when 3. fx - fy = 6x + 6y + 2 f (x, y) = x - 2y x + 2y 4. fo - fy = 6x - 10y + 2 1. fr = 5. fz - fy = 6x + 6y -4 (a + 2y)2 6. fx - fy = 10x - 10y + 2 2. fr = (a+ 2y)2 4y 010 10.0 points 3. fr = (x + 2y) 2 Determine whether the partial derivatives by 4. f1 = fx, fy of f are positive, negative or zero at the (x + 2y)2 point P on the graph of f shown in By 5. fr = ( + 2y) 2 3x 6. fx = (x + 2y)2 012 10.0 points Determine fr when f(x, y) = cos(3y - z) - Isin(3y - I) . 1. fr = x sin(3y - I) 2. fx = x cos(3y - I)alnujaidi (sga593) - Homework 11 - israel - (53215) 4 3. fr = -xsin(3y - x) 015 10.0 points 4. fr = -x cos(3y - X) Find the value of fr and fy at (1, -1) when 5. fz = - cos(3y - x) - x sin(3y - I) f (x, y) = ry - + 5x2 + 32. 6. fz = -2sin(3y - x) - I cos(3y - I) 1. fig -1= 8, fy (1,-1= -4 7. fx = 2sin(3y - x) - rcos(3y - x) 8. fx = x cos(3y - x) - sin(3y - z) 2. fig -1= 7, fula, -1)= -3 013 10.0 points 3. fig-)= 12, fy (1.-1)= 0 Find the slope in the r-direction at the point P(0, 2, f(0, 2)) on the graph of f when 4. fig-) = 12, fy (1-1)= -4 f(x, y) = 2(2x + y)e -zy . (1,-1 ) = -8, ful(1-1) = 0 1. slope = -10 10.0 points 2. slope = -12 Determine fry when 3. slope = -4 4. slope = -6 f (x, y) = -xtan-' (). 5. slope = -8 1. fry = (2 + y2)2 014 10.0 points Determine fr when 2. fry = (z2 + 72)2 f (x, y) = (x +2y) ex/v. 3. fry = - 2(x2 + y2) 1. fo = #+1 ex/ 4. fry = 2(x2 + y?) 2. fx = (=+1) ex/y 5. fry = 3. fr = -1 ex/v 2(x2 + y? ) 4. fr = (~+3) ez/u 6. fry = (a2 + y2 ) 2 5. fr = =-3 ez/y 017 10.0 points Find ut when 6. fx = (#-3) exiv u = resin0.\f