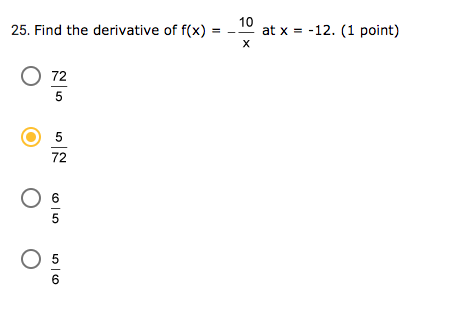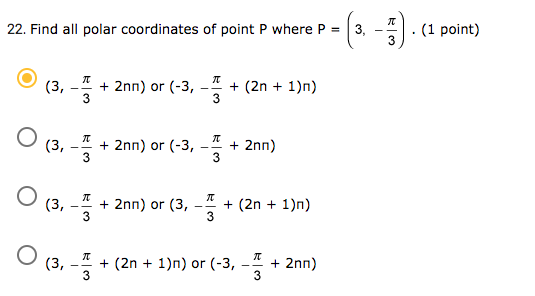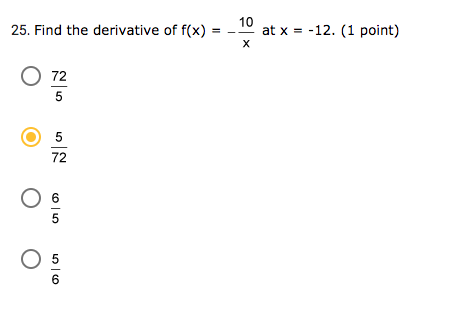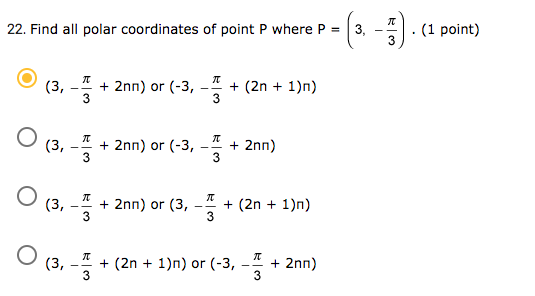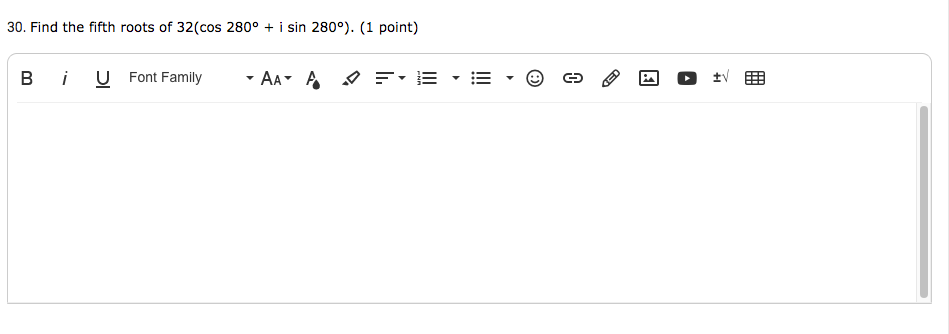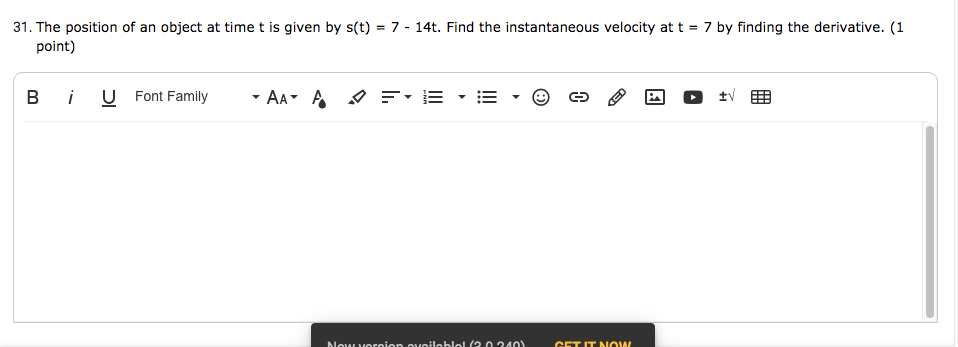
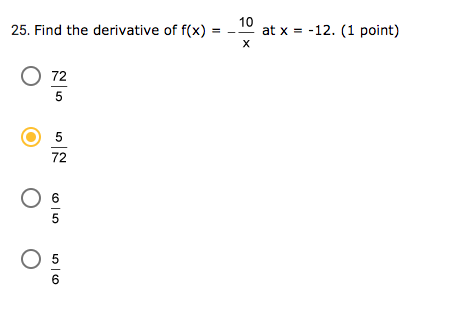
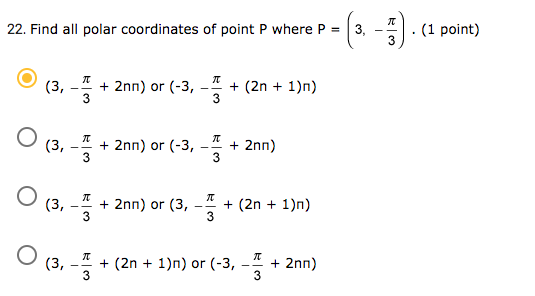



Hello! For problems number 22 and 25 below, I just need you to check my answer and tell me which one is correct, I do not need an explanation.
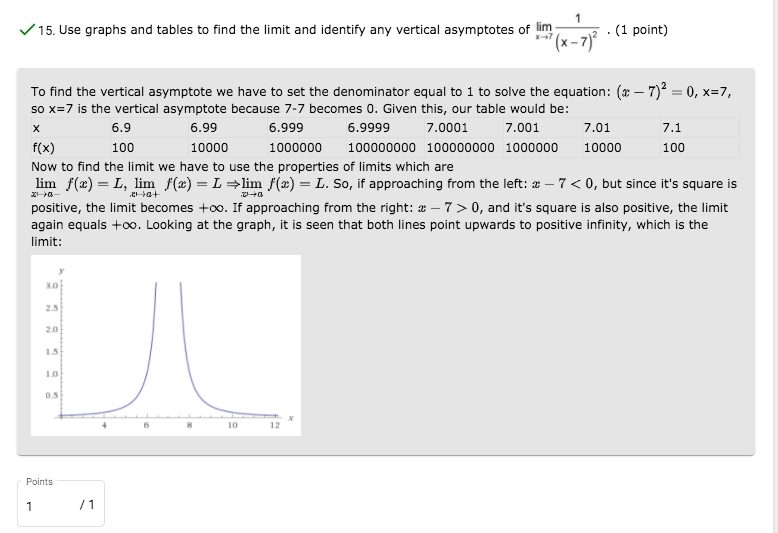
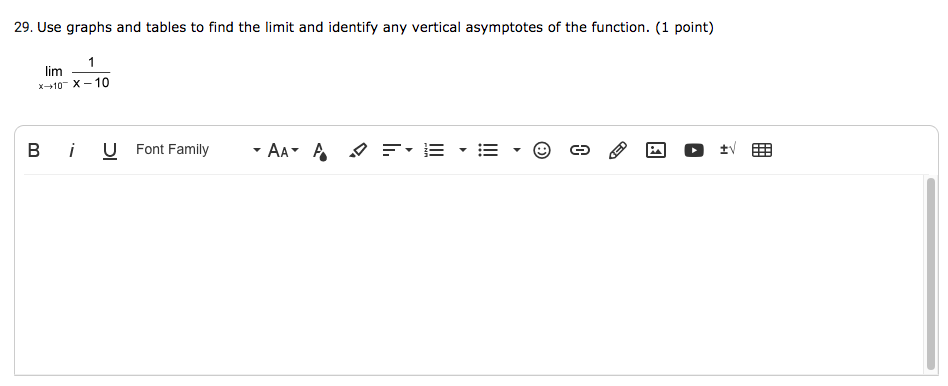
Let's look at the function f(x) = * -2 x 3 - 4 We will use this function to evaluate the limit as x approaches 0, as x approaches 2, and as x approaches -2, using a graphical and a numerical approach. Example #1 10 1 -2 From the graph shown above, we can see that lim - x-2 - 1 *-+0 X3 - 4 2' Now let's create a table of values to analyze this limit numerically. Calculator Tip: Type y1= (x-2)/(x^2-4) on your Ti-83. Parentheses are needed around the entire numerator, as well as the entire denominator. You can use the table feature of your calculator to generate the x and corresponding y values, by setting the independent variable (x) to "Ask" and the dependent variable (y) to 'Auto' under Table Set Up. -0.3 -0.2 -0.1 0 0.1 0.2 0.3 f(x) 0.58824 0.55556 0.52632 0.5 0.47619 0.45455 0.43478 The limit of this function as x values get close to 0 is the number that the y value is approaching or reaches. The table confirms our graphical analysis that the limit is 1/2. Example #2 0 1 From the graph shown above, we can see that lim - X - 2 *+2 x2 -4 is a positive value smaller than V/2. Now let's create a table of values to analyze this limit numerically and find a more accurate answer.1 15. Use graphs and tables to find the limit and identify any vertical asymptotes of lim (x - 7)2 . (1 point) To find the vertical asymptote we have to set the denominator equal to 1 to solve the equation: (* - 7)' = 0, x=7, so x=7 is the vertical asymptote because 7-7 becomes 0. Given this, our table would be: X 6.9 6.99 6.999 6.9999 7.0001 7.001 7.01 7.1 f(x) 100 10000 1000000 100000000 100000000 1000000 10000 100 Now to find the limit we have to use the properties of limits which are lim f(2) = L, lim f(*) = L =lim f(@) = L. So, if approaching from the left: @ - 7 0, and it's square is also positive, the limit again equals too. Looking at the graph, it is seen that both lines point upwards to positive infinity, which is the limit: 210 15 10 12 Points 1 /129. Use graphs and tables to find the limit and identify any vertical asymptotes of the function. (1 point) lim x-10- X - 10 B i U Font Family AAA D =. UN-\f. (1 point) 22. Find all polar coordinates of point P where P = 3, A A + (2n + 1)n) (3, + 2nn) or (-3, - 3 O (3, + 2nn) or (-3, + 2nn) 3 O + 2nn) or (3, - + (2n + 1)n) (3, O + (2n + 1)n) or (-3, - + 2nn) (3, 330. Find the fifth roots of 32(cos 280 + i sin 2809). (1 point) Font Family - AA A UN-31. The position of an object at time t is given by s(t) = 7 - 14t. Find the instantaneous velocity at t = 7 by finding the derivative. (1 point) B i U Font Family - AA A DE tvCorrect Answer: z1= 2(cos 56 deg + i sin 56 deg) z2= 2(cos 128 deg + i sin 128 deg) z3 = 2(cos 200 deg + i sin 200 deg) z4 = 2(cos 272 deg+ i sin 272 deg) z5 = 2(cos 344 deg+ i sin 344 deg) Step-by-step explanation: De Moivre's Theorem--> e^i theta = cos theta + i sin theta The fifth root of 32 is 2 and 280/5 is 56 z1= 2(cos 56 deg + i sin 56 deg) 360deg/ 5 =72 deg (If it was asking for cubed root u would do 360/3. whatever the root is you divide that by 360) z2= 2(cos 56 + 72) + (i sin 56 + 72) z2= 2(cos 128 deg + i sin 128 deg) z3 = 2(cos 128 + 72) + ( i sin 128 + 72) 23 = 2(cos 200 deg + i sin 200 deg) 24 = 2(cos 200 + 72) + (i sin 200 + 72) z4 = 2(cos 272 deg + i sin 272 deg) 25 = 2(cos 272 + 72) + (i sin 272 + 72) z5 = 2(cos 344 deg + i sin 344 deg) deg means degreesUse the formula: r^(1)*[ cos( (theta+360*k) ) + i sin( (theta+360*k) ) ] where k = 0,1,2,3,4 First 5th root: k = 0 r*(1)*[ cos( (theta+360*k) ) + i*sin( (theta+360*k) ) ] (32)^(1/5)*[ cos( (280+360*k)/5 ) + i*sin( (280+360*k)/5 ) ] (32)^(1/5)*[ cos( (280+360*0)/5 ) + i*sin( (280+360*0)/5 ) ] 2*[ cos( (280+360*0)/5 ) + i*sin( (280+360*0)/5 ) ] 2"[ cos( (280+0)/5 ) + i*sin( (280+0)/5 ) ] 2*[ cos( 280/5 ) + i*sin( 280/5 ) ] 2*[ cos( 56 ) + i'sin( 56 ) ] Second 5th root: k = 1 r*(1)*[ cos( (theta+360*k) ) + i*sin( (theta+360*k) ) ] (32)^(1/5)*[ cos( (280+360*k)/5 ) + i*sin( (280+360*k)/5 ) ] (32)^(1/5)*[ cos( (280+360*1)/5 ) + i*sin( (280+360*1)/5 ) ] 2*[ cos( (280+360*1)/5 ) + i*sin( (280+360*1)/5 ) ] 2"[ cos( (280+360)/5 ) + i*sin( (280+360)/5 ) ] 2*[ cos( 640/5 ) + i'sin( 640/5 ) ] 2 [ cos( 128 ) + i sin( 128 ) ] Third 5th root: k = 2 r*(1)*[ cos( (theta+360*k) ) + i*sin( (theta+360*k) ) ] (32)^(1/5)*[ cos( (280+360*k)/5 ) + i*sin( (280+360*k)/5 ) ] (32)^(1/5)*[ cos( (280+360*2)/5 ) + i*sin( (280+360*2)/5 ) ] 2*[ cos( (280+360*2)/5 ) + i*sin( (280+360*2)/5 ) ] 2"[ cos( (280+720)/5 ) + i*sin( (280+720)/5 ) ] 2"[ cos( 1000/5 ) + i'sin( 1000/5 ) ] 2"[ cos( 200 ) + i'sin( 200 ) ] Fourth 5th root: k = 3 r*(1)*[ cos( (theta+360*k) ) + i*sin( (theta+360*k) ) ] (32)^(1/5)*[ cos( (280+360*k)/5 ) + i*sin( (280+360*k)/5 ) ] (32)^(1/5)*[ cos( (280+360*3)/5 ) + i*sin( (280+360*3)/5 ) ] 2*[ cos( (280+360*3)/5 ) + i*sin( (280+360*3)/5 ) ] 2*[ cos( (280+1080)/5 ) + i'sin( (280+1080)/5 ) ] 2"[ cos( 1360/5 ) + i*sin( 1360/5 ) ] 2*[ cos( 272 ) + i*sin( 272 ) ] Fifth 5th root: k = 4 r^(1)*[ cos( (theta+360*k) ) + i*sin( (theta+360*k) ) ] (32)^(1/5)*[ cos( (280+360*k)/5 ) + i*sin( (280+360*k)/5 ) ] (32)^(1/5)*[ cos( (280+360*4)/5 ) + i*sin( (280+360*4)/5 ) ] 2*[ cos( (280+360*4)/5 ) + i*sin( (280+360*4)/5 ) ] 2"[ cos( (280+1440)/5 ) + i*sin( (280+1440)/5 ) ] "*[ cost 1720/5) + i*sin( 1720/5)1EXPLANATION The complex number given to us is in the polar form, 32(cos 280' + i sin 280") The fifth root is 32 (cos 280 + i sin 280) # This is equal to: 2(cos 280 + i sin 280) According to the DeMoivre's Theorem, (cos 0 + isin 0) = (cos 20 + i sin 20) We now use the DeMoivre's Theorem to obtain: 2( cos 280 + i sin 280) # = 2(cos { x 280 + isin { x 280) 2(cos 280 + i sin 280) = 2(cos 56 + isin 56)