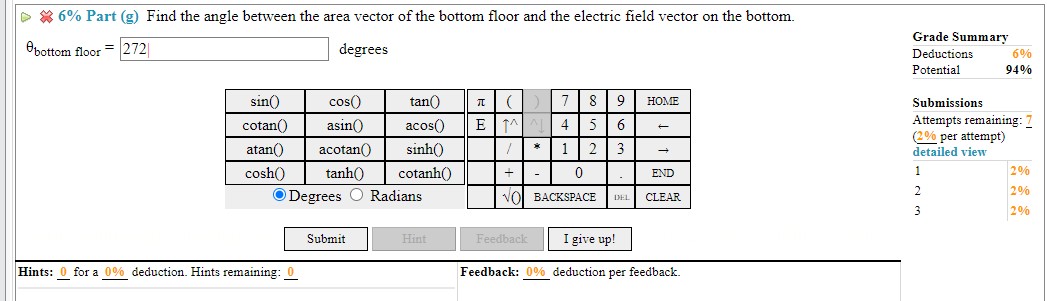
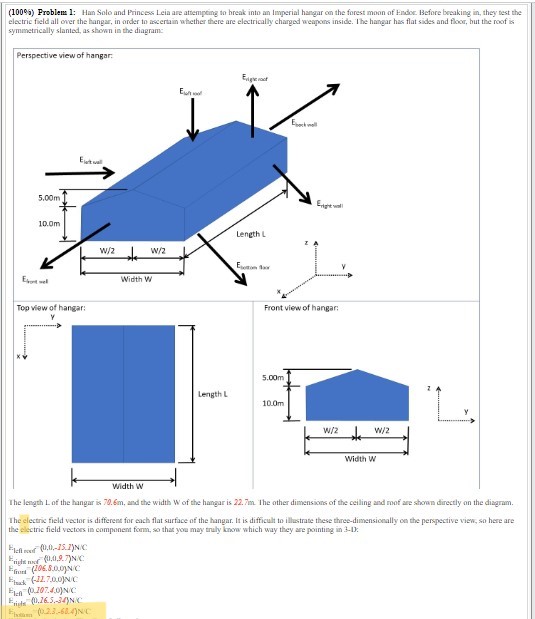
Hello I need help with part and g and h. I tried using the inverse tangent for the components of the flux given but my answer is wrong. The components for part g is highlighted in yellow in the first picture. For part h the angle I found that is needed to compute the electric flux is 156.23 degrees but my answer was wrong for that as well. Please show and explain steps to the answer and why the answer is what it is.

(100%%) Problem 1: Han Solo and Princess Leia are attempting to break into an Imperial hangar on the forest moon of Endor Before breaking in, they best the electric field all over the hangar, in order in ascertain whether there are electrically charged weapons inside. The hangar has flat sides and floor, but the roof is symmetrically slanted, as shown in the diagrams Perspective view of hangar. 5.00m T 10.0m Length L W/7 W/2 Width W Top view of hangar: Front view of hangar: 5.00m Length L 1 10 0m L........ W/2 W/2 Width W Width W The length L of the hangar is 74.5m, and the width Wof the hangar is 23. 7m. The other dimensions of the ceiling and mof are shown directly on the diagram. The electric field vector is different for each flat surface of the hangar. It is difficult in illustrate these three-dimensionally on the perspective view, so here are the electric field vectors in component form, so that you may truly know which way they are pointing in 3-13. fun (106. 50.0)N/C Bits (.165.-34 NICG* 6% Part (h) Find the electric flux passing through the left roof. Grade Summary Pleft roof = 11073.37 Nm-/C Deductions 6% Potential 94% sin() cos() tanO 7 8 HOME Submissions asin() acos() TA AT 4 5 6 Attempts remaining: 7 cotan() (2% per attempt) atan() acotan() sinh() 1 2 3 detailed view cosho tanh() cotanh() 2% T END O Degrees O Radians BACKSPACE CLEAR W N 2%% Submit Hint Feedback I give up! Hints: 1 for a 0% deduction. Hints remaining: 0 Feedback: 0% deduction per feedback. You can use the angle you found earlier to do the polar dot product formula.*6% Part (g) Find the angle between the area vector of the bottom floor and the electric field vector on the bottom. ebottom floor = 272 Grade Summary degrees Deductions 6% Potential 94% sino cos() tan() 7 HOME Submissions cotan() asin() acoso F TA 4 5 Attempts remaining: (2% per attempt) atan() acotan() sinh() 1 2 3 detailed view cosh( tanh( cotanh() 0 END 2%% O Degrees O Radians VO BACKSPACE CLEAR 2% W N 2% Submit Hint Feedback I give up! Hints: 0 for a 0% deduction. Hints remaining: _0 Feedback: 0% deduction per feedback