

Hello,
I need help with the following questions as I do not know how to answer them because we did'nt cover the topics in great depths in class with our teacher:
Please find them attached below:
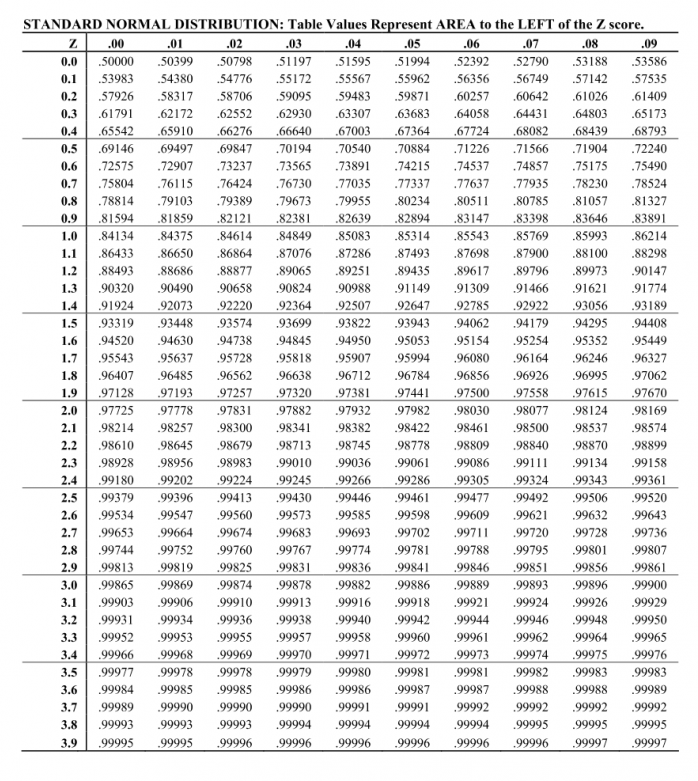
STANDARD NORMAL DISTRIBUTION: Table Values Represent AREA to the LEFT of the Z score. Z .00 01 02 .03 04 05 .06 07 08 .09 0.0 50000 50399 50798 51 197 51595 $1994 52392 52790 53188 53586 0.1 .53983 54380 54776 55172 .55567 55962 56356 56749 57142 57535 0.2 57926 58317 .58706 59095 .59483 59871 60257 .60642 61026 61409 0.3 61791 .62172 62552 .62930 63307 63683 .64058 .64431 64803 65173 0.4 65542 65910 66276 66640 67003 67364 67724 68082 68439 68793 0.5 69146 69497 69847 70194 70540 70884 71226 71566 71904 72240 0.6 72575 72907 73237 .73565 73891 .74215 74537 .74857 75175 75490 0.7 75804 76115 .76424 76730 77035 .77337 77637 77935 78230 78524 0.8 .78814 .79103 79389 .79673 79955 80234 .80511 80785 .81057 81327 0.9 81594 81859 .82121 82381 82639 82894 83147 83398 83646 83891 1.0 84134 .84375 84614 84849 85083 .85314 .85543 85769 85993 86214 1.1 86433 86650 .86864 87076 87286 87493 87698 87900 .88100 88298 1.2 88493 88686 88877 .89065 .89251 89435 89617 .89796 .89973 90147 1.3 .90320 90490 90658 90824 90988 91149 91309 91466 91621 91774 1.4 91924 92073 92220 92364 92507 92647 92785 92922 93056 93189 1.5 .93319 93448 93574 93699 .93822 93943 94062 94179 94295 94408 1.6 .94520 94630 .94738 .94845 94950 95053 .95154 95254 .95352 95449 1.7 95543 95637 95728 95818 95907 95994 96080 .96164 96246 .96327 1.8 96407 96485 96562 96638 .96712 .96784 96856 96926 96995 97062 1.9 97128 97193 97257 97320 97381 9744 97500 97558 97615 97670 2.0 97725 97778 97831 97882 97932 97982 98030 98077 98124 98169 2.1 98214 98257 98300 98341 .98382 98422 98461 98500 98537 98574 2.2 98610 98645 98679 98713 98745 98778 98809 98840 .98870 98899 2.3 98928 98956 98983 99010 99036 99061 .99086 99111 99134 99158 2.4 99180 99202 99224 99245 99266 99286 99305 99324 99343 99361 2.5 99379 99396 99413 99430 99446 99461 99477 99492 99506 99520 2.6 99534 99547 99560 99573 99585 99598 99609 99621 99632 99643 2.7 99653 99664 99674 .99683 99693 99702 99711 99720 99728 99736 2.8 .99744 99752 99760 .99767 99774 99781 99788 .99795 99801 99807 2.9 99813 99819 99825 99831 99836 9984 99846 99851 99856 99861 3.0 99865 99869 99874 99878 99882 99886 99889 99893 99896 99900 3.1 99903 99906 99910 .99913 99916 99918 .99921 99924 .99926 99929 3.2 99931 99934 99936 99938 99940 99942 99944 99946 99948 99950 3.3 99952 99953 99955 .99957 99958 99960 99961 99962 99964 99965 3.4 99966 99968 99969 99970 99971 99972 99973 99974 99975 99976 3.5 99977 99978 99978 99979 .99980 99981 99981 99982 99983 99983 3.6 99984 99985 99985 99986 99986 99987 99987 99988 99988 99989 3.7 .99989 .99990 99990 .99990 99991 .99991 99992 99992 99992 99992 3.8 99993 99993 99993 99994 99994 99994 99994 99995 99995 99995 3.9 99995 99995 99996 99996 99996 99996 99996 99996 99997 .99997STANDARD NORMAL DISTRIBUTION: Table Values Represent AREA to the LEFT of the Z score. Z .00 01 02 .03 04 05 .06 07 08 .09 0.0 50000 50399 50798 51 197 51595 $1994 52392 52790 53188 53586 0.1 .53983 54380 54776 55172 .55567 55962 56356 56749 57142 57535 0.2 57926 58317 .58706 59095 .59483 59871 60257 .60642 61026 61409 0.3 61791 .62172 62552 .62930 63307 63683 .64058 .64431 64803 65173 0.4 65542 65910 66276 66640 67003 67364 67724 68082 68439 68793 0.5 69146 69497 69847 70194 70540 70884 71226 71566 71904 72240 0.6 72575 72907 73237 .73565 73891 .74215 74537 .74857 75175 75490 0.7 75804 76115 .76424 76730 77035 .77337 77637 77935 78230 78524 0.8 .78814 .79103 79389 .79673 79955 80234 .80511 80785 .81057 81327 0.9 81594 81859 .82121 82381 82639 82894 83147 83398 83646 83891 1.0 84134 .84375 84614 84849 85083 .85314 .85543 85769 85993 86214 1.1 86433 86650 .86864 87076 87286 87493 87698 87900 .88100 88298 1.2 88493 88686 88877 .89065 .89251 89435 89617 .89796 .89973 90147 1.3 .90320 90490 90658 90824 90988 91149 91309 91466 91621 91774 1.4 91924 92073 92220 92364 92507 92647 92785 92922 93056 93189 1.5 .93319 93448 93574 93699 .93822 93943 94062 94179 94295 94408 1.6 .94520 94630 .94738 .94845 94950 95053 .95154 95254 .95352 95449 1.7 95543 95637 95728 95818 95907 95994 96080 .96164 96246 .96327 1.8 96407 96485 96562 96638 .96712 .96784 96856 96926 96995 97062 1.9 97128 97193 97257 97320 97381 9744 97500 97558 97615 97670 2.0 97725 97778 97831 97882 97932 97982 98030 98077 98124 98169 2.1 98214 98257 98300 98341 .98382 98422 98461 98500 98537 98574 2.2 98610 98645 98679 98713 98745 98778 98809 98840 .98870 98899 2.3 98928 98956 98983 99010 99036 99061 .99086 99111 99134 99158 2.4 99180 99202 99224 99245 99266 99286 99305 99324 99343 99361 2.5 99379 99396 99413 99430 99446 99461 99477 99492 99506 99520 2.6 99534 99547 99560 99573 99585 99598 99609 99621 99632 99643 2.7 99653 99664 99674 .99683 99693 99702 99711 99720 99728 99736 2.8 .99744 99752 99760 .99767 99774 99781 99788 .99795 99801 99807 2.9 99813 99819 99825 99831 99836 9984 99846 99851 99856 99861 3.0 99865 99869 99874 99878 99882 99886 99889 99893 99896 99900 3.1 99903 99906 99910 .99913 99916 99918 .99921 99924 .99926 99929 3.2 99931 99934 99936 99938 99940 99942 99944 99946 99948 99950 3.3 99952 99953 99955 .99957 99958 99960 99961 99962 99964 99965 3.4 99966 99968 99969 99970 99971 99972 99973 99974 99975 99976 3.5 99977 99978 99978 99979 .99980 99981 99981 99982 99983 99983 3.6 99984 99985 99985 99986 99986 99987 99987 99988 99988 99989 3.7 .99989 .99990 99990 .99990 99991 .99991 99992 99992 99992 99992 3.8 99993 99993 99993 99994 99994 99994 99994 99995 99995 99995 3.9 99995 99995 99996 99996 99996 99996 99996 99996 99997 .999976. Body mass index (BMI) is calculated by dividing a person's weight by the square of their height. The BMI for middle aged men at risk for diabetes follows an approximately normal distribution with a population mean = 24 kg/m2 and population standard deviation of 2.7 kg/mz. A sample of 58 men are randomly selected from the population. The mean BMI from this sample is 25 kg/ml. 3. Construct a 95% confidence interval. (1 mark) b. Describe what your 95% condence interval means. (1 mark) c. Identify a null and alternative hypothesis for a twosided test. (1 mark) d. Calculate a z score for this data and depict the z score on a standard normal curve. You are welcome to draw the distribution on your computer or draw it by hand. Include the image in your word document. (2 marks) e. Using the standard normal chart in Module 03 Section 02, identify the area to the right for your 2 score, assuming this is a two-sided test. (1 mark) f. Based on your ndings, would you reject or fail to reject the null hypothesis with a significance level of or = 0.05. (1 mark) g. Describe the two types of error you can make when you conduct a hypothesis test. (2 marks) Module 03 Homework Problems Note About Module 03 Homework: Module 03 homework is slightly different from previous modules. This week you do not need to use Excel or SPSS as these questions are more about connecting concepts and practicing some calculations/logic by hand. For this reason, you only need to submit one summary document for your Module 03 homework. Be sure to show the formulas/your work for each question and upload the document to Elentra as a PDF. 1. Describe standard deviation and standard error and when you would use error bars with one versus the other (1 mark) 2. Describe the three basic operations that can be performed on probability events, write out their formulas, and provide an example of when you would use each one. (3 marks) 3. You are in the process of conducting a chart audit on the records of patients who received a total hip or total knee replacement (assume these are independent events). Their data is summarized in the table by age. What is the probability of: a. Being over age 70? (1 mark) b. Having a knee replacement? (1 mark) c. Being over age 70 m having a knee replacement? (1 mark) d. Being under age 70 or having a hip replacement? (1 mark) Table 1. Distribution of Joint Re lacements b A - e 4. Describe the properties of a standard normal distribution. (1 mark) 5. Dene point estimation, interval estimation, and hypothesis testing. Describe how these concepts are similar and how they are different? (2 marks)












