Hello, I need help with these practice questions pleasee . Could you do them on a piece of paper or on the practice questions sheets so I can better understand.

Thank you

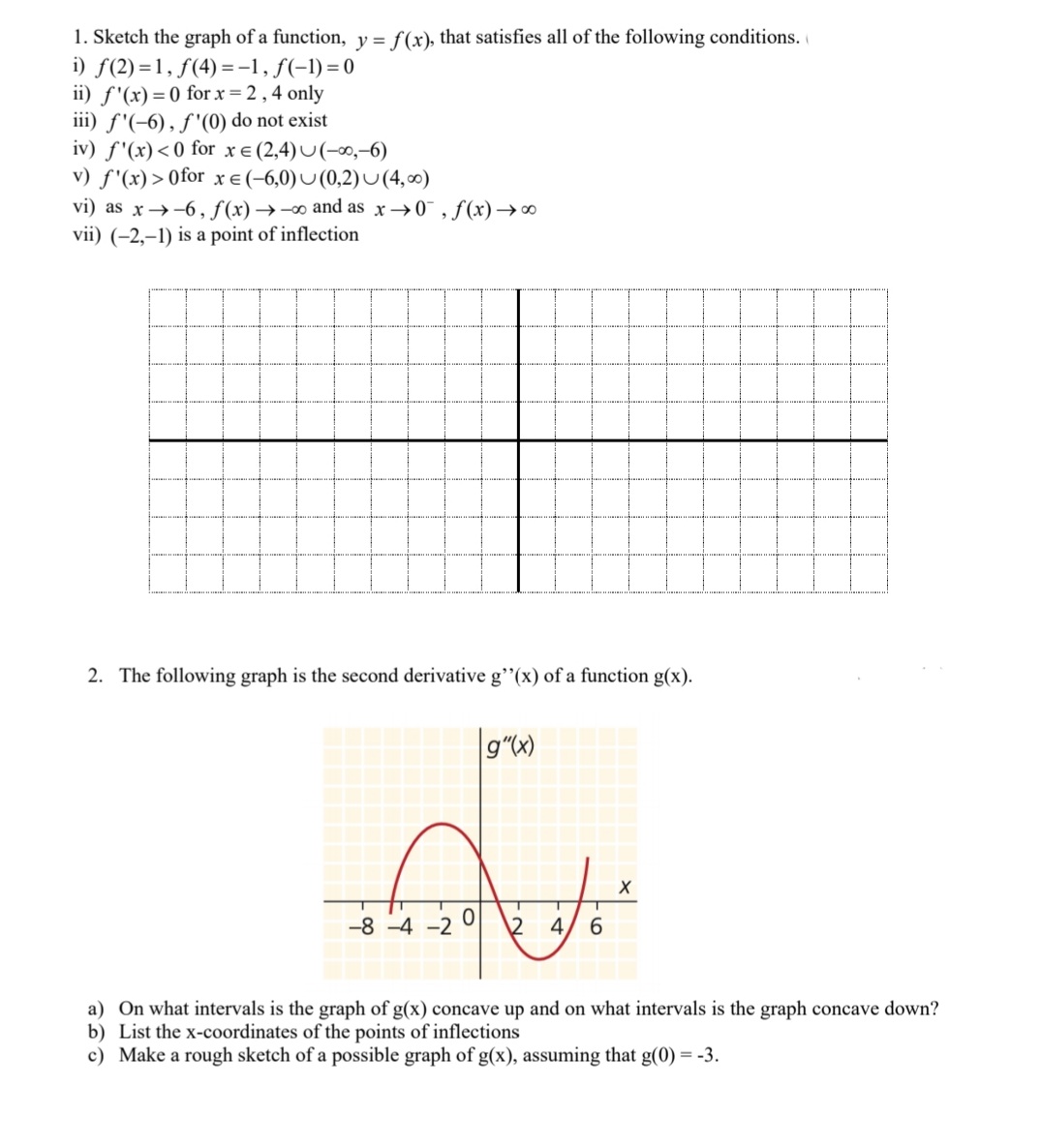
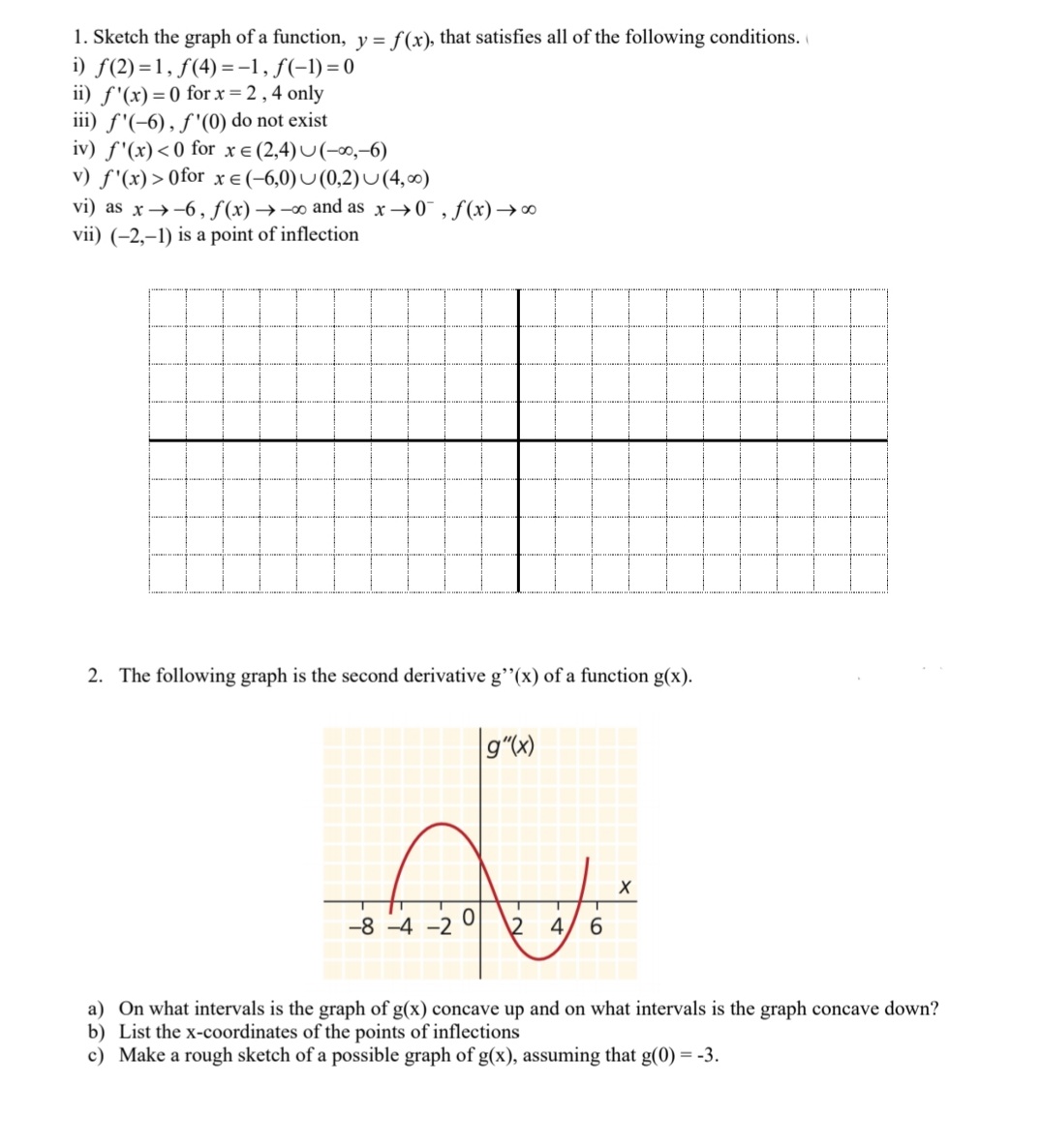
1. Let f(x) = x4+ 10x3 + 36x2 + 12x + 2. For which value(s) of x does f (x) have a point of inflection? a. x = -3 C. x = -2 b. x = -3 and x = -2 d. x = -3,x = -2 and x = 0 2. If f"(x) > 0, what can you tell about the graph of f (x)? a. f' (x) is increaing, f (x) is concave up c. f' (x) is increaing, f(x) is concave down b. f' (x) is decreaing, f (x) is concave up d. f' (x) is decreaing, f (x) is concave down 3. Let f (x) = - x2-4x-12 x2-8x+12 Determine the equation(s) of the vertical asymptote(s)? a. x = 2 C. x = -2 b. x = 6 d. x = 2 and x = 6 4. Let f'(x) = (x - 3)3(x + 4)(x2 + 1). What are the critical number(s)? a. x =-1 C. x = -4, x = 3 b. x = -4 x = -4,x = -1, x = 3 5. Let f (x) = = -4x+8 x2-3x-10 Determine the equation(s) of the horizontal asymptote? a. y = 0 C. y = -4 b. no horizontal asymptote d. x = -2 and x = 53. Find the intervals of increase and decrease algebraically with a sign diagram for: f (x) = 4. Find the point(s) of inflection and intervals of concavity using a sign diagram for: f(x) = 3x4 - 16x3 + 24x2 - 9 5. Let f(x) = ax3 + bx2 + cx + d. Determine the values of a, b, c, and d if f (x) has a point of inflection at (0, 2) and a local maximum at (2, 6).6. For the function f ( x) = x . Determine each of the following for f (x): l (I - 1) 2 a) 'I ) Intercepts: 1)) Equation of Horizontal asymptote: c) Equation of Vertical asymptote(s): d) Intervals of increase 1' decrease and any local maximum and minimum points e) Intervals of concavity and any points of inection f) Sketch the graph of the function, clearly labeling all information from a) to e). 1. Sketch the graph of a function, y = f(x), that satisfies all of the following conditions. ( i) f (2) = 1, f(4) = -1, f(-1) =0 ii) f'(x) = 0 for x = 2 , 4 only iii) f'(-6) , f'(0) do not exist iv) f'(x) 0for x E (-6,0) (0,2) (4, 00) vi) as x -> -6, f(x) -> co and as x -> 0- , f(x) -co vii) (-2,-1) is a point of inflection 2. The following graph is the second derivative g"(x) of a function g(x). g" (x ) -8 4 0 a) On what intervals is the graph of g(x) concave up and on what intervals is the graph concave down? b) List the x-coordinates of the points of inflections c) Make a rough sketch of a possible graph of g(x), assuming that g(0) = -3